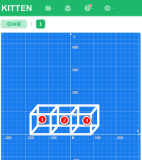
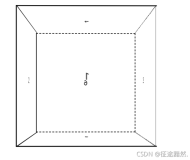
效果如下图所示:我们实际上使用了 2D 来模拟 3D 效果。
应用程序启动时,默认只绘制一个立方体,因此我们在初始绘制的函数里,只执行动态绘制 X 方向的立方体这一个逻辑。因为默认 X 方向的立方体只有1个,所以只会绘制一个立方体。
每次动态绘制 X 方向的立方体,都会首先计算 X 方向立方体初始定点的 X 和 Y 坐标。之所以每次绘制前都会重新计算,是因为我们的应用允许用户动态添加新的立方体,即总的立方体个数会动态增加。
为了确保初始立方体在屏幕正中绘制,我们计算 x 方向立方体初始顶点 X 坐标的公式如上图所示,用立方体棱长乘以 X 方向的立方体个数再除以2.
从左到右绘制全部立方体的逻辑是通过下图的重复执行积木完成的。在调用绘制单个立方体积木之前,确保变量 X方向动态立方体X坐标的值被正确设置。
在循环体内,变量 X方向动态立方体X坐标 的值被累加,步长为立方体棱长。如果想实现拆分效果,在这个步长基础上再增加50即可。
拆分效果如下:
在事件响应函数里,需要依次绘制X,Y 和 Z 三个方向的立方体。
Y 方向立方体的绘制比较简单,在第一个点的立方体绘制完毕后,回到点1,将点1的朝向调整旋转角度,然后移动斜边变量代表的步数,即到点2.
到了点2之后,调用动态绘制Y方向立方体 函数,在里面每次调用从左到右绘制全部立方体函数之前,先设置 X 方向立方体初始顶点的 X 和 Y 坐标。这个坐标通过首先回到最初始计算出来的原点,然后每次沿着旋转角度方向,移动斜边长度的 N 倍来到达新的起始点。此处 N 即为 y 方向的循环次数。