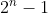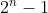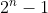1.进位计数制及其相互转化

1.基数：每个数码位用到的不同符号的个数

二进制：0、1（逢2进1）

八进制：0、1、2、3、4、5、6、7（逢8进1）(3位2进制）

十六进制：0、1、2、3、4、5、6、7、8、9、A 、B、C、D、E、F（逢16进1）（4位2进制）

2.转换成数值：各位数码按位权相加

3.二进制的优势：

①可以用两个稳定状态的物理器件表示

②0、1对应逻辑假和真，方便实现逻辑运算

③方便使用逻辑门电路实现算术运算

4.真值：实际带正负号的数值（人类习惯的样子）

机器数：把正负号数字化的数（机器中数字的存放形式）

机器字长 = 通用寄存器位数 = ALU位数 = 计算机一次最多进行计算的位数

2.无符号整数的表示

1.没有符号位，即不需要添加0或者1表示正负

2.n位（n bit）所能表示的范围位 0 -

最小的数：全0

最大的数：全1

2.1.无符号整数的加法

从最低位开始，按位相加，并往更高位进位

2.2.无符号整数

①被减数不变，减数全部按位取反，取反后加1

快速方法：从右往左找到第一个1，这个1左边的全部位按位取反

这么做的原因是：加法电路易于实现，造价便宜，减法电路实现困难，造价昂贵

②从最低位开始，按位相加，并往更高位进位

3.带符号整数

3.1.原码表示

1.符号位1bit：0/1对应负/正；剩下位数表示真值的绝对值

2.若机器字长为n + 1bit：原码表示范围为 -  ~ + （真值部分全1）

3.真值0有两种形式（符号位不同，真值相同）：设有8bit

+0：0000 0000

-0：1000 0000

4.原码的缺点：符号位不能参与运算，需要特别设定电路（因此设计补码）  

3.2.反码和补码

1.正数：不变

负数：反码：符号位不变，数值位按位取反；补码：反码的基础上末位+1

2.原码、反码、补码的第一位都是符号位

3.补码转换为反码：补码→原码→反码

4.原码和补码相互转换：从右往左找到第一个1，这个1左边的所有数值位按位取反

3.3.补码的加法

从最低位开始，按位相加（符号位参与运算），并往更高位进位

3.4.补码的减法

1.原理：将减法转化为加法：A - B = A + （-B）

2.将B转换为-B：全部位（包括符号位）按位取反，末位+1（同无符号数的减法）

快速方法：从右往左找到第一个1，这个1左边的全部位按位取反（区别于原码和补码转换）

3.5.原码、补码加法减法小结

3.6.原码、反码、补码和移码基本特性总结

设共有8bit：

1.原码和反码的范围为-127 ~ +127。其中：

①原码的最小值-127（1111 1111） = 反码真值-0 （1111 1111）

②原码真值-0（1000 0000）= 反码最小值-127（1000 0000）

2.补码和移码范围为-128 ~ +127。其中：

①补码和移码真值0只有+0

补码：0000 0000；移码：1000 0000

②补码 -128：1000 0000；移码-128：0000 0000

3.判断溢出：手算十进制，是否超出合法范围

3.7.移码

1.补码的基础上符号位取反

2.移码只能表示整数（原码、反码、补码都可以表示小数）

3.移码的范围：-128 ~ + 127（和补码相同）

4.移码的特性：真值单调增大，适用于硬件电路比较大小（浮点数阶码）

4.定点小数

1.某位的位权的大小根据和小数点相对位置决定

2.定点整数：默认小数点在最后一位的右边（原码、反码、补码、移码）

定点小数：默认小数点在符号位的右边（原码、反码、补码）

3.定点小数的原码、补码、反码的转换、加法和减法和定点整数一致

4.若对整数进行扩展，在符号位和数值位中间加0；若对小数进行扩展，在数值位的右边加0（原码）