第8章 二叉树
1. 二叉树理论基础
二叉树种类
(1)满二叉树
(2)完全二叉树
(3)二叉搜索树
或称二叉查找树
中序遍历是递增序列
(4)平衡二叉搜索树
二叉树的存储方式
可以链式存储,也可以顺序存储
链式存储用指针,顺序存储用数组
顺序存储的元素在内存是连续分布的,链式存储则是通过指针把分布在散落在各个地址的结点串联在一起
用数组来存储二叉树如何遍历的呢?
如果父节点的数组下标是 i,那么它的左孩子就是 i * 2 + 1,右孩子就是 i * 2 + 2。
二叉树的遍历
深度优先遍历:都有递归和迭代两种方法
- 前序遍历:中左右
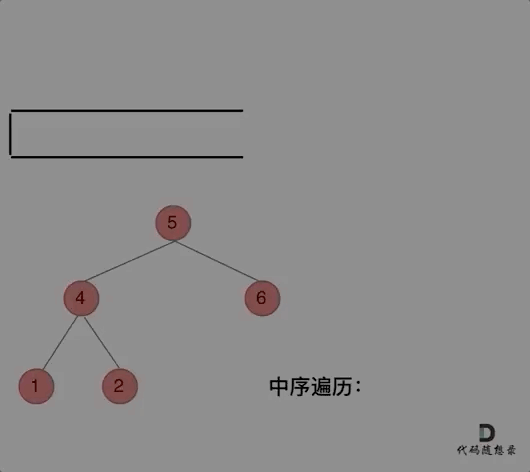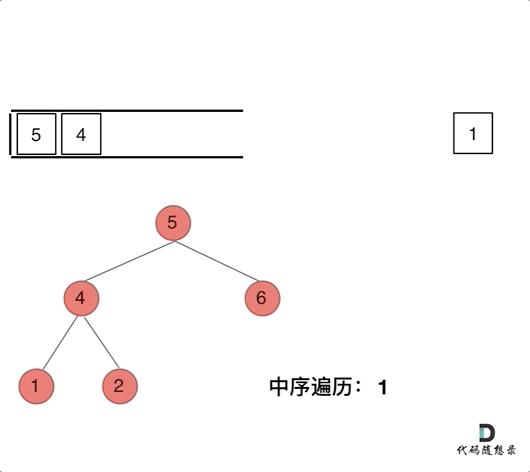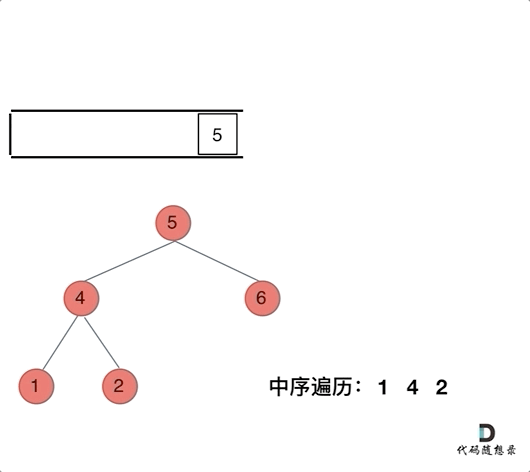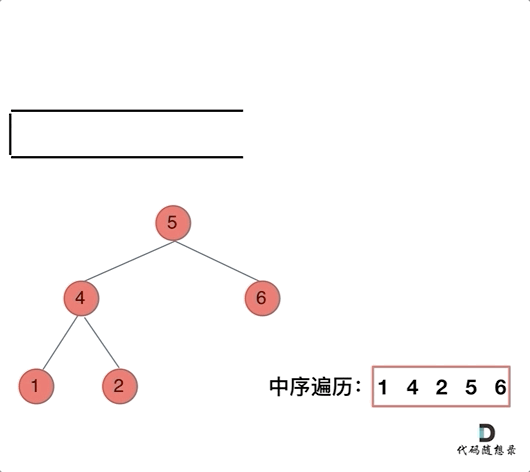
- 中序遍历:左中右
- 后序遍历:左右中
广度优先遍历
- 层次遍历(迭代法)
二叉树的定义
struct TreeNode{ int val; TreeNode *left; TreeNode *right; TreeNode() : val(0), left(nullptr), right(nullptr) {} TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} }
2. 二叉树的遍历
二叉树的递归遍历
递归三要素:
- 确定递归函数的参数和返回值:
void preorder(TreeNode *root, vector<int>& res)
- 确定终止条件:
if(cur == nullptr) return;
- 确定单层递归的逻辑
时间复杂度:O(n)
空间复杂度:O(n)
class Solution { public: void preorder(TreeNode *root, vector<int> &res) { if (root == nullptr) return; res.push_back(root->val); //中 preorder(root->left, res); //左 preorder(root->right, res); //右 } vector<int> preorderTraversal(TreeNode *root) { vector<int> res; preorder(root, res); return res; } };
实现不同的遍历顺序通过修改单层递归的逻辑实现
二叉树的迭代遍历
通过栈实现
时间复杂度:O(n)
空间复杂度:O(n)
(1)前序遍历
class Solution { public: vector<int> preorderTraversal(TreeNode* root) { vector<int> res; stack<TreeNode*> s; if(root == nullptr) return res; s.push(root); //压入根结点 while (!s.empty()){ //入栈是 根右左 TreeNode* node = s.top(); s.pop(); res.push_back(node->val); //中 if (node->right) stk.push(node->right); //右 if (node->left) stk.push(node->left); //左 } return res; } };
(2)中序遍历
class Solution { public: vector<int> inorderTraversal(TreeNode* root) { vector<int> res; stack<TreeNode*> s; TreeNode* cur = root; while (cur != nullptr || !s.empty()) { if (cur != nullptr) { // 指针来访问节点,访问到最底层 s.push(cur); // 将访问的节点放进栈 cur = cur->left; // 左 } else { cur = s.top(); s.pop(); // 从栈里弹出的数据,就是要处理的数据(放进result数组里的数据) res.push_back(cur->val); // 中 cur = cur->right; // 右 } } return res; } };
(3)后序遍历
跟前序的很像,中序是三个当中差距最大的
class Solution { public: //后续迭代最难,有些结点反复进出栈 vector<int> postorderTraversal(TreeNode* root) { vector<int> res; stack<TreeNode*> s; if (root == nullptr) return res; s.push(root); while(!s.empty()){ auto node = s.top(); s.pop(); res.push_back(node->val); //中 //这两步相对于前序 顺序换了 if(node->left) s.push(node->left); //左 if(node->right) s.push(node->right); //右 } reverse(res.begin(), res.end()); // 将结果反转之后就是左右中的顺序了 return res; } };
二叉树的层序遍历
通过队列实现
class Solution { public: vector<vector<int>> levelOrder(TreeNode* root) { vector <vector <int>> res; if (root == nullptr) return res; //排除空二叉树情况 queue <TreeNode*> q; q.push(root); //根结点入队 while (!q.empty()) { int currentLevelSize = q.size(); //记录当前层的结点个数 res.push_back(vector <int>()); for (int i = 1; i <= currentLevelSize; ++i) { auto node = q.front(); //获取队头元素 q.pop(); //删除队头元素 res.back().push_back(node->val); //往ret的最后一个容器中压元素 if (node->left) q.push(node->left); if (node->right) q.push(node->right); } } return res; } };
107. 二叉树的层序遍历 II【中等】
思路:把层序遍历的结果reverse一下再输出
reverse(res.begin(), res.end());
完整代码不记录
199. 二叉树的右视图【中等】
思路:层次遍历存储每层最后一个元素
class Solution { public: vector<int> rightSideView(TreeNode* root) { vector<int> res; if (root == nullptr) return res; queue<TreeNode*> q; q.push(root); while (!q.empty()) { int currentSize = q.size(); for (int i = 1; i <= currentSize; ++i) { auto node = q.front(); q.pop(); if (i == currentSize) res.push_back(node->val); if (node->left) q.push(node->left); if (node->right) q.push(node->right); } } return res; } };
637. 二叉树的层平均值【简单】
class Solution { public: vector<double> averageOfLevels(TreeNode* root) { vector<double> res; if (root == nullptr) return res; queue<TreeNode*> q; q.push(root); while (!q.empty()) { int currentSize = q.size(); double num = 0; //注意是double for (int i = 1; i <= currentSize; ++i) { auto node = q.front(); q.pop(); num += node->val; if (node->left) q.push(node->left); if (node->right) q.push(node->right); } res.push_back(num / currentSize); } return res; } };
429. N 叉树的层序遍历【中等】
/* // Definition for a Node. class Node { public: int val; vector<Node*> children; Node() {} Node(int _val) { val = _val; } Node(int _val, vector<Node*> _children) { val = _val; children = _children; } }; */ class Solution { public: vector<vector<int>> levelOrder(Node* root) { vector<vector<int>> res; if(root == nullptr) return res; queue<Node*> q; q.push(root); while(!q.empty()){ res.push_back(vector<int> ()); int currentSize = q.size(); for(int i = 1; i <= currentSize; ++i){ auto node = q.front(); q.pop(); res.back().push_back(node->val); for(auto i : node->children){ q.push(i); } } } return res; } };
515. 在每个树行中找最大值【中等】
class Solution { public: vector<int> largestValues(TreeNode* root) { vector<int> res; if(root == nullptr) return res; queue<TreeNode*> q; q.push(root); while(!q.empty()){ int currentSize = q.size(); int nowMax = INT_MIN; for(int i = 1; i <= currentSize; ++i){ auto node = q.front(); q.pop(); nowMax = max(node->val, nowMax); if(node->left) q.push(node->left); if(node->right) q.push(node->right); } res.push_back(nowMax); } return res; } };
116. 填充每个节点的下一个右侧节点指针【中等】
/* // Definition for a Node. class Node { public: int val; Node* left; Node* right; Node* next; Node() : val(0), left(NULL), right(NULL), next(NULL) {} Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {} Node(int _val, Node* _left, Node* _right, Node* _next) : val(_val), left(_left), right(_right), next(_next) {} }; */ class Solution { public: Node* connect(Node* root) { if (root == nullptr) return root; queue<Node*>q; q.push(root); while (!q.empty()) { int current_level_size = q.size(); for (int i = 1; i <= current_level_size; ++i) { auto node = q.front(); q.pop(); if (i < current_level_size) node->next = q.front(); //实现next指向 else node->next = NULL; if (node->left) q.push(node->left); if (node->right) q.push(node->right); } } return root; } };
117. 填充每个节点的下一个右侧节点指针 II【中等】
与116题做法一模一样,这里写了代码随想录的解法;116题写的是我自己习惯的解法。
class Solution { public: Node* connect(Node* root) { if(root == nullptr) return root; queue<Node*> q; q.push(root); while (!que.empty()) { int currentSize = que.size(); Node* nodePre; Node* node; for (int i = 1; i <= currentSize; i++) { if (i == 0) { nodePre = q.front(); // 取出一层的头结点 q.pop(); node = nodePre; continue; } node = q.front(); q.pop(); nodePre->next = node; // 本层前一个节点next指向本节点 nodePre = nodePre->next; if (node->left) q.push(node->left); if (node->right) q.push(node->right); } nodePre->next = NULL; // 本层最后一个节点指向NULL } return root; } };
104. 二叉树的最大深度【简单】
class Solution { public: int maxDepth(TreeNode* root) { int res = 0; if(root == nullptr) return res; queue<TreeNode*> q; q.push(root); while(!q.empty()){ int currentSize = q.size(); for(int i = 1; i <= currentSize; ++i){ auto node = q.front(); q.pop(); if(node->left) q.push(node->left); if(node->right) q.push(node->right); } res++; } return res; } };
111. 二叉树的最小深度【简单】
class Solution { public: int minDepth(TreeNode* root) { int res = 0; if (root == nullptr) return res; queue <TreeNode*> q; q.push(root); //根结点入队 while (!q.empty()) { int currentLevelSize = q.size(); //记录当前层的结点个数 res++; for (int i = 1; i <= currentLevelSize; i++) { //队列弹出当前层所有元素 并压入下一层所有元素 auto node = q.front(); q.pop(); if (node->left == nullptr && node->right == nullptr) { return res; } if (node->left) q.push(node->left); if (node->right) q.push(node->right); } } return res; } };
3. 翻转二叉树
226. 翻转二叉树【简单】
相同题目:剑指 Offer 27. 二叉树的镜像
迭代:
广度优先遍历,即层次遍历
class Solution { public: TreeNode* invertTree(TreeNode* root) { if (root == nullptr) return root; queue<TreeNode*> q; q.push(root); while (!q.empty()) { auto node = q.front(); q.pop(); swap(node->left, node->right); if (node->left) q.push(node->left); if (node->right) q.push(node->right); } return root; } };
深度优先遍历就是把queue换成stack
递归:
递归三部曲:
- 确定递归函数的参数和返回值:
TreeNode* invertTree(TreeNode* root)
- 确定终止条件:
if(root == nullptr) return NULL
- 确定单层递归的逻辑
class Solution { public: TreeNode* invertTree(TreeNode* root) { if(root == nullptr) return NULL; swap(root->left, root->right); invertTree(root->left); invertTree(root->right); return root; } };
上面是递归的前序遍历
递归的中序遍历这里是不行的
4. 对称二叉树
101. 对称二叉树【简单】
相同题目:剑指 Offer 28. 对称的二叉树
迭代:
class Solution { public: bool isSymmetric(TreeNode* root) { if(root == nullptr) return true; queue<TreeNode*> q; q.push(root->left); q.push(root->right); while(!q.empty()){ auto leftNode = q.front(); q.pop(); auto rightNode = q.front(); q.pop(); if(leftNode == nullptr && rightNode == nullptr) continue; //少了报错 if(leftNode == nullptr && rightNode != nullptr) return false; if(leftNode != nullptr && rightNode == nullptr) return false; if(leftNode->val != rightNode->val) return false; q.push(leftNode->left); q.push(rightNode->right); q.push(leftNode->right); q.push(rightNode->left); } return true; } };
同样的queue改成stack也可以,其他原封不动
递归:
递归三部曲:
- 确定递归函数的参数和返回值:
bool compare(TreeNode* left, TreeNode* right)
- 确定终止条件
- 确定单层递归逻辑
class Solution { public: bool compare(TreeNode* left, TreeNode* right){ //1.确定递归函数的参数 //2.确定终止条件 if(left == nullptr && right == nullptr) return true; else if(left == nullptr && right != nullptr) return false; else if(left != nullptr && right == nullptr) return false; else if(left->val != right->val) return false; //3.返回值 return compare(left->left, right->right) && compare(left->right, right->left); } bool isSymmetric(TreeNode* root) { if(root == nullptr) return true; return compare(root->left, root->right); } };
100. 相同的树【简单】
递归:
class Solution { public: bool isSameTree(TreeNode* p, TreeNode* q) { if(p == nullptr && q == nullptr) return true; else if(p == nullptr && q != nullptr) return false; else if(p != nullptr && q == nullptr) return false; else if(p->val != q->val) return false; return isSameTree(p->left, q->left) && isSameTree(p->right, q->right); } };
迭代:
class Solution { public: bool isSameTree(TreeNode* p, TreeNode* q) { if(p == nullptr && q == nullptr) return true; if(p == nullptr || q == nullptr) return false; queue<TreeNode*> que; que.push(p); que.push(q); while(!que.empty()){ auto pNode = que.front(); que.pop(); auto qNode = que.front(); que.pop(); if(pNode->val != qNode->val) return false; auto pLeft = pNode->left, pRight = pNode->right, qLeft = qNode->left, qRight = qNode->right; if(pLeft == nullptr && qLeft != nullptr) return false; else if(pLeft != nullptr && qLeft == nullptr) return false; else if(pLeft != nullptr && qLeft != nullptr){ que.push(pLeft); que.push(qLeft); } if(pRight == nullptr && qRight != nullptr) return false; else if(pRight != nullptr && qRight == nullptr) return false; else if(pRight != nullptr || qRight != nullptr) { que.push(pRight); que.push(qRight); } } return true; } };