🎉考前冲刺🎉
✏️记笔记:
并查集属于高级算法的一种,但是根据历年省赛真题来看,只要掌握了该模板,那几乎就是送分题哦,我将从这三道经典的并查集题目来带大家学习并查集模板!!
🎠1、合根植物
🎯问题描述
编辑
样例输入
5 4 16 2 3 1 5 5 9 4 8 7 8 9 10 10 11 11 12 10 14 12 16 14 18 17 18 15 19 19 20 9 13 13 17
样例输出
5
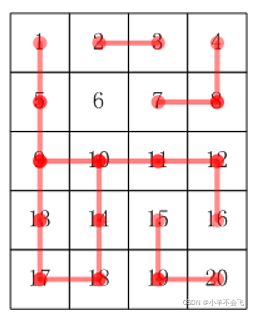
其合根情况参考下图:
编辑
package Day_Day_work; import java.util.Scanner; /** * @author yx * @date 2022-03-25 20:18 */ public class 合根植物___并查集 { static int[] father=new int[1000010]; public static void main(String[] args) { Scanner scanner = new Scanner(System.in); int m=scanner.nextInt(); int n=scanner.nextInt(); int k=scanner.nextInt(); for (int i = 1; i <=m*n ; i++) {//初始化父节点 father[i]=i; } for (int i = 0; i < k; i++) { int a=scanner.nextInt(); int b=scanner.nextInt(); if(Findfather(a)!=Findfather(b)){ union(a,b); } } int ans=0; for (int i = 1; i <=m*n ; i++) { if(father[i]==i){ ans++; } } System.out.println(ans); } private static int Findfather(int a) {//寻找祖宗节点 if(a==father[a]){ return a; } /** * 路径压缩 */ // return Findfather(father[a]); father[a]=Findfather(father[a]);//父节点设置为根节点 return father[a]; } private static void union(int a, int b) {//合并 a=Findfather(father[a]); b=Findfather(father[b]); // if(Findfather(a)!=Findfather(b)){ // father[Findfather(a)]=b; // } if(a!=b){ father[a]=b; } } }
💦题解分析:
(1)这是一道非常适合入门的并查集题目,简单易懂,模板十分清晰
(2)我来给大家分析一下模板的三要素:
1、初始化每一个父节点(即i的父节点为i自身)
2、Findfather()函数,用来寻找该节点的“祖宗”节点(一直往上寻找根节点)
3、union()函数,用来合并两个节点(将a的祖宗节点设置为b,ab就属于一个集合了)
(3)博主解释下面这行代码,当我们不断地合并节点后,每一个“子节点”的“父节点”都最终指向根节点,那么我们怎么判断一共有多少个集合呢?我们不难发现一个集合中只有其根节点的父节点是指向自己的,那就好办了,当有一个节点其父节点等于自己,那么就代表有一个集合,也就是下面的这行记录集合数量的代码了
if(father[i]==i) { ans++; }
🎏2、亲戚
🎯问题描述
编辑
输入
6 5 3 1 2 1 5 3 4 5 2 1 3 1 4 2 3 5 6
输出
Yes Yes No
package Day_Day_work; import java.util.Scanner; /** * @author yx * @date 2022-04-04 19:06 */ public class 亲戚__并查集 { static int fa[]=new int[5010]; public static void main(String[] args) { Scanner scanner = new Scanner(System.in); int n=scanner.nextInt(); int m=scanner.nextInt(); int q=scanner.nextInt(); for (int i = 1; i <=n ; i++) {//初始化亲戚 fa[i]=i; } for (int i = 1; i <=m ; i++) { int a=scanner.nextInt(); int b=scanner.nextInt(); gx(a,b); } for (int i = 1; i <=q ; i++) { int a=scanner.nextInt(); int b=scanner.nextInt(); if(find(a)==find(b)){ System.out.println("Yes"); } else { System.out.println("No"); } } } static void gx(int x,int y){//合并操作 fa[find(x)]=find(y); return; } static int find(int x){//找祖先 if(fa[x]==x){ return x; } fa[x]=find(fa[x]); return fa[x]; } }
💦题解分析:
(1)该题是来源于洛谷的一道蛮经典的并查集入门题
(2)该题官方给的答案是用按秩合并来做的,博主为了让大家更好地理解并查集模板,采用传统解法
(3)聪明的小伙伴不难发现该题代码中的:
gx()函数就是上道题目的union()函数
find函数就是上道题目的Findfather()函数
(4)套路可谓是一毛一样,即使我们不会按秩合并,用常规的并查集模板也可以给它秒了
(5)注意看find()函数中使用了一行代码进行路径压缩(父节点直接指向根节点),优化了查找的复杂度
fa[x]=find(fa[x]);
🧵3、七段码
🎯问题描述
编辑
package Day_Day_work.problem; /** * @author yx * @date 2022-04-03 23:12 */ public class 七段码__dfs__并查集 { static int e[][]=new int[8][8];//存储灯管的连通情况 static int fa[]=new int[8];//并查集的父节点 static boolean isTrue[]=new boolean[8]; static int ans=0; public static void main(String[] args) { //连边建图 //a b c d e f g //1 2 3 4 5 6 7 //e[i][j]=1表示i灯光和j灯光是相互连接的 e[1][2]=e[1][6]=1; e[2][1]=e[2][7]=e[2][3]=1; e[3][2]=e[3][4]=e[3][7]=1; e[4][3]=e[4][5]=1; e[5][4]=e[5][6]=e[5][7]=1; e[6][1]=e[6][5]=e[6][7]=1; dfs(1); System.out.println(ans); } static void dfs(int n){ if(n==8){//出口,遍历了每一盏灯的情况 for (int i = 1; i <=7 ; i++) {//初始化每一个父节点 fa[i]=i; } for (int i = 1; i <=7 ; i++) { for (int j = 1; j <=7 ; j++) { if(isTrue[i]&&isTrue[j]&&e[i][j]==1){//如果当前两盏相互连接的灯处于打开的状态则放在一个集合里 fa[find(i)]=find(j);//合并操作 } } } int cnt=0;//用来记录联通情况 for (int i = 1; i <=7 ; i++) { if(isTrue[i]&&fa[i]==i){ cnt++; } } //当有且仅有一种联通亮灯情况的时候才合法,这个时候ans++ if(cnt==1)ans++; return; } isTrue[n]=true;//当前第n盏灯是打开的 dfs(n+1);//递归 isTrue[n]=false;//当前第n盏灯是关闭的 dfs(n+1); } static int find(int x){//寻找父节点 if(x==fa[x]){ return x; }else { fa[x]=find(fa[x]); return fa[x]; } } }
💦题解分析:
(1)这个题目是一道填空题,比较综合(dfs+并查集),考察难度不输一般大题
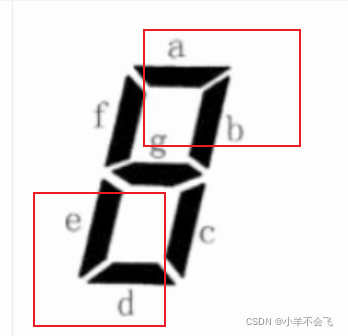
(2)用二维数组模拟灯泡i和灯泡j的相邻情况(相邻为1)
(3)dfs枚举每一个灯的亮灭组成的所有情况(一共有2^7种可能)
(4)解释一下下面这行代码,当有且仅有一种联通亮灯情况的时候才合法,这个时候ans++
举个例子:
编辑
a和b构成一种联通;e和d构成一种联通,cnt=2,这个时候不符合题意,直接pass
if(cnt==1)ans++; return;
🚀写在最后
距离蓝桥杯只有四天啦!!
博主争取再更一篇BFS的押题篇,希望大家多多支持!✨
最后,博主想送给大家一句话:
你逆光而来
配得上所有的美好
编辑