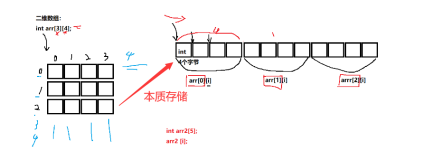
//下面两个用例我们后面单独拿出来讲哈!
数组的应用实例1:三子棋
数组的应用实例2:扫雷游戏
这两个会专门写在后面
3. 数组越界
数组的下标是有范围限制的。
数组的下规定是从 0 开始的,如果数组有 n 个元素,最后一个元素的下标就是 n-1 。
所以数组的下标如果小于 0 ,或者大于 n-1 ,就是数组越界访问了,超出了数组合法空间的访问。
C 语言本身是不做数组下标的越界检查,编译器也不一定报错,但是编译器不报错,并不意味着程序就是正确的,
所以程序员写代码时,最好自己做越界的检查。
#include <stdio.h> int main () { int arr [ 10 ] = { 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 }; int i = 0 ; for ( i = 0 ; i <= 10 ; i ++ ) { printf ( "%d\n" , arr [ i ]); // 当 i 等于 10 的时候,越界访问了 } return 0 ; }
二维数组的行和列也可能存在越界。
4. 数组作为函数参数
往往我们在写代码的时候,会将数组作为参数传个函数,比如:我要实现一个冒泡排序(这里要讲算法思想函数
将一个整形数组排序。
那我们将会这样使用该函数:
4.1 冒泡排序函数的错误设计
冒泡排序思路:
对于冒泡排序的大体思路,就是第一个元素去和后面所有的元素去比较大小比如 1 5 3 7 4 这几个数一开始1和5必(我们实现升序),然后再和3比然后往后比(到4)发现,都比1大,1就说明排序好了,然后5再和3比,发现比他大,就交换变成 1 3 5 7 4,然后再3和7比,再和4比,我们比的时候只在同一个位置比,然后后面谁小我们就把谁换过来,一直到最后一个数我们就发现假设有n个数,我们就要进行n-1趟 每一趟比较的次数就是 n-1 再 -i(因为前面的数已经排好了所以减去)
// 方法 1 : #include <stdio.h> void bubble_sort ( int arr []) { int sz = sizeof ( arr ) / sizeof ( arr [ 0 ]); // 这样对吗? int i = 0 ; for ( i = 0 ; i < sz - 1 ; i ++ ) { int j = 0 ; for ( j = 0 ; j < sz - i - 1 ; j ++ ) { if ( arr [ j ] > arr [ j + 1 ]) { int tmp = arr [ j ]; arr [ j ] = arr [ j + 1 ]; arr [ j + 1 ] = tmp ; } } } } int main () { int arr [] = { 3 , 1 , 7 , 5 , 8 , 9 , 0 , 2 , 4 , 6 }; bubble_sort ( arr ); // 是否可以正常排序? for ( i = 0 ; i < sizeof ( arr ) / sizeof ( arr [ 0 ]); i ++ ) { printf ( "%d " , arr [ i ]); } return 0 ; }
方法 1 ,出问题,那我们找一下问题,调试之后可以看到 bubble_sort 函数内部的 sz ,是 1 。
难道数组作为函数参数的时候,不是把整个数组的传递过去?
4.2 数组名是什么?
#include <stdio.h> int main () { int arr [ 10 ] = { 1 , 2 , 3 , 4 , 5 }; printf ( "%p\n" , arr ); printf ( "%p\n" , & arr [ 0 ]); printf ( "%d\n" , * arr ); // 输出结果 return 0 ; } 结论: 数组名是数组首元素的地址。(有两个例外) 如果数组名是首元素地址,那么: int arr [ 10 ] = { 0 }; printf ( "%d\n" , sizeof ( arr ));
为什么输出的结果是: 40 ?
补充:
1. sizeof( 数组名 ) ,计算整个数组的大小, sizeof 内部单独放一个数组名,数组名表示整个数组。
2. & 数组名,取出的是数组的地址。 & 数组名,数组名表示整个数组。
除此 1,2 两种情况之外,所有的数组名都表示数组首元素的地址。
4.3 冒泡排序函数的正确设计
当数组传参的时候,实际上只是把数组的首元素的地址传递过去了。
所以即使在函数参数部分写成数组的形式: int arr[] 表示的依然是一个指针: int *arr 。
那么,函数内部的 sizeof(arr) 结果是 4 。
如果 方法 1 错了,该怎么设计?
// 方法 2 void bubble_sort ( int arr [], int sz ) // 参数接收数组元素个数 { // 代码同上面函数 } int main () { int arr [] = { 3 , 1 , 7 , 5 , 8 , 9 , 0 , 2 , 4 , 6 }; int sz = sizeof ( arr ) / sizeof ( arr [ 0 ]); bubble_sort ( arr , sz ); // 是否可以正常排序? for ( i = 0 ; i < sz ; i ++ ) { printf ( "%d " , arr [ i ]); } return 0 ; }
对于递归的补充:
//这是作者自己在查的时候发现了一位我认为讲的很细的博主 帅地 写的一篇文章,但是可能不太适合小白看,因为我自己也看了,是讲了很多内容的,所以我就把递归内容拷贝过来了,后面有链接哈,他也出了很多递归的题,大家可以看一下哈!下面是拷贝过来的哈:
递归的三大要素
第一要素:明确你这个函数想要干什么
对于递归,我觉得很重要的一个事就是,这个函数的功能是什么,他要完成什么样的一件事,而这个,是完全由你自己来定义的。也就是说,我们先不管函数里面的代码什么,而是要先明白,你这个函数是要用来干什么。
例如,我定义了一个函数
// 算 n 的阶乘(假设n不为0)
int f(int n){
}
这个函数的功能是算 n 的阶乘。好了,我们已经定义了一个函数,并且定义了它的功能是什么,接下来我们看第二要素。
第二要素:寻找递归结束条件
所谓递归,就是会在函数内部代码中,调用这个函数本身,所以,我们必须要找出递归的结束条件,不然的话,会一直调用自己,进入无底洞。也就是说,我们需要找出当参数为啥时,递归结束,之后直接把结果返回,请注意,这个时候我们必须能根据这个参数的值,能够直接知道函数的结果是什么。
例如,上面那个例子,当 n = 1 时,那你应该能够直接知道 f(n) 是啥吧?此时,f(1) = 1。完善我们函数内部的代码,把第二要素加进代码里面,如下
// 算 n 的阶乘(假设n不为0) int f(int n){ if(n == 1){ return 1; } }
有人可能会说,当 n = 2 时,那我们可以直接知道 f(n) 等于多少啊,那我可以把 n = 2 作为递归的结束条件吗?
当然可以,只要你觉得参数是什么时,你能够直接知道函数的结果,那么你就可以把这个参数作为结束的条件,所以下面这段代码也是可以的。
// 算 n 的阶乘(假设n>=2) int f(int n){ if(n == 2){ return 2; } }
注意我代码里面写的注释,假设 n >= 2,因为如果 n = 1时,会被漏掉,当 n <= 2时,f(n) = n,所以为了更加严谨,我们可以写成这样:
// 算 n 的阶乘(假设n不为0) int f(int n){ if(n <= 2){ return n; } }