原文链接:http://tecdat.cn/?p=22226
两个随机变量之间的相依性问题备受关注,相依性(dependence)是反映两个随机变量之间关联程度的一个概念(点击文末“阅读原文”获取完整代码数据)。
它与相关性(correlation)有区别,常用的相关性度量是Pearson相关系数,它只度量了两个随机变量之间的线性关系,其值不仅依赖于它们的Copula函数,而且还依赖它们的边缘分布函数。
直观地说,Copula函数就是两个(或多个)随机变量的联合分布可以表示为它们的边缘分布函数的函数,这个函数就是Copula函数,它与随机变量的边缘分布没有关系,所反映的是两个(多个)随机变量之间的“结构”,这种结构包含了两个随机变量相依性的全部信息。
Joe(1990)尾部相依性指数
Joe(1990)提出了一个(强)尾部相依性指数。例如,对于下尾,可以考虑
也就是
- 上下尾(经验)相依性函数
我们的想法是绘制上面的函数。定义
下尾
对上尾来说,其中是 与 ,相依的生存copula ,即
其中
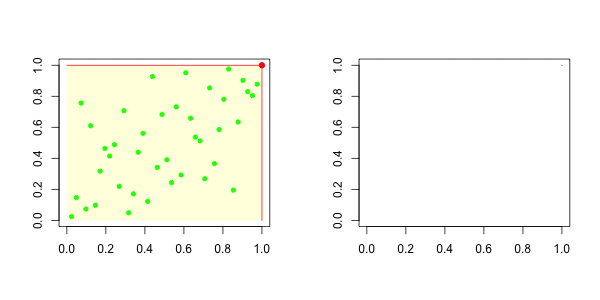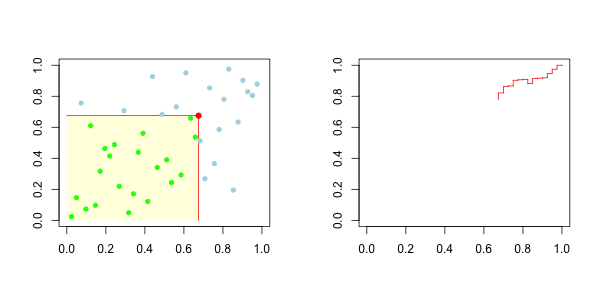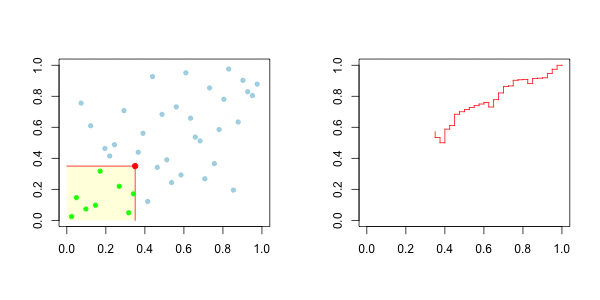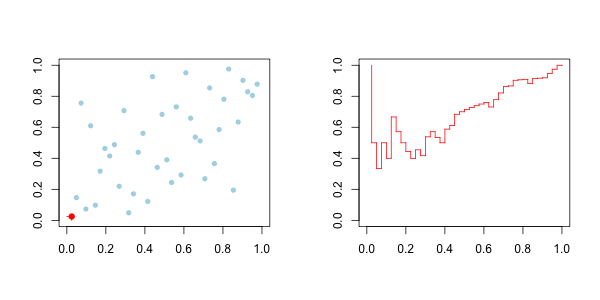
现在,我们可以很容易地推导出这些函数的经验对应关系,即:
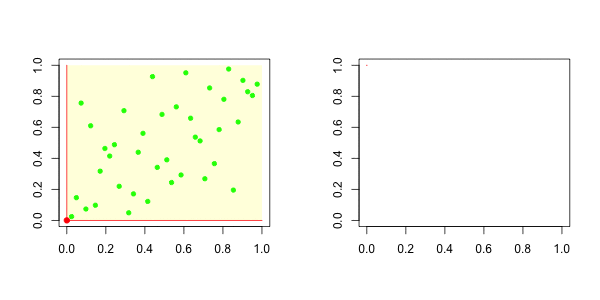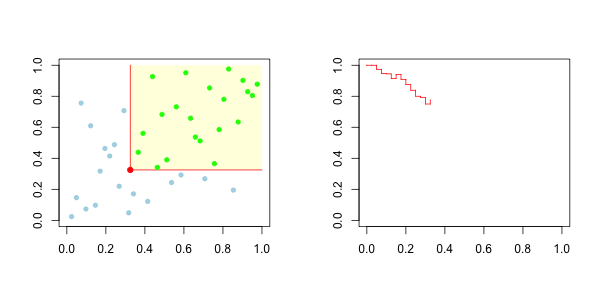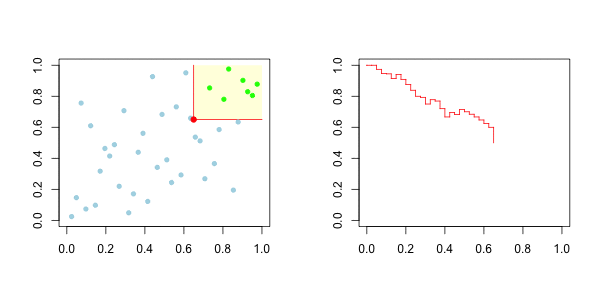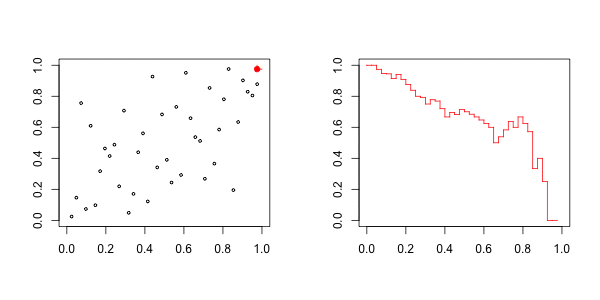
因此,对于上尾,在右边,我们有以下图形
而对于下尾,在左边,我们有
点击标题查阅往期内容
01
02
03
04
损失赔偿数据
Copula函数在经济、金融、保险等领域有广泛的应用.早在1998年Frees和Valdez(1998)研究了索赔额与管理费之间的关系,采用了Copula函数对其进行刻画并应用于保费的定价。
对于代码,考虑一些真实的数据,比如损失赔偿数据集。
损失赔偿费用数据有1,500个样本和2个变量。这两栏包含赔偿金付款(损失)和分配的损失调整费用(alae)。后者是与解决索赔相关的额外费用(如索赔调查费用和法律费用)。
我们的想法是,在左边绘制下尾函数,在右边绘制上尾函数。
现在,我们可以将这个图形,与一些具有相同Kendall's tau参数的copulas图形进行比较
高斯copulas
如果我们考虑高斯copulas 。
> copgauss=normalCopula(paramgauss) > Lga=function(z) pCopula(c(z,z),copgauss)/z > Rga=function(z) (1-2*z+pCopula(c(z,z),copgauss))/(1-z) > lines(c(u,u+.5-u\[1\]),c(Lgs,Rgs)
Gumbelcopula
或Gumbel的copula。
> copgumbel=gumbelCopula(paramgumbel, dim = 2) > lines(c(u,u+.5-u\[1\])
置信区间
但是由于我们没有任何置信区间,所以仍然很难得出结论(即使看起来Gumbel copula比Gaussian copula更适合)。一个策略可以是从这些copula曲线中生成样本,并可视化。对于高斯copula曲线
> nsimul=500 > for(s in 1:nsimul){ + Xs=rCopula(nrow(X),copgauss) + Us=rank(Xs\[,1\])/(nrow(Xs)+1) + Vs=rank(Xs\[,2\])/(nrow(Xs)+1) + lines(c(u,u+.5-u\[1\]),MGS\[s,\],col="red")
包括–逐点–90%的置信区间
> Q95=function(x) quantile(x,.95) > lines(c(u,u+.5-u\[1\]),V05,col="red",lwd=2)
高斯copula曲线
Gumbel copula曲线
尽管统计收敛的速度会很慢,评估底层的copula 曲线是否具有尾部相依性简单。尤其是当copula 曲线表现出尾部独立性的时候。比如考虑一个1000大小的高斯copula 样本。这是我们生成随机方案后得到的结果。
或者我们看一下左边的尾巴(用对数比例)
现在,考虑10000个样本。
在这些图上,如果极限是0,或者是某个严格的正值,是相当难以断定的(同样,当感兴趣的值处于参数的支持边界时,这是一个经典的统计问题)。所以,一个简单的想法是考虑一个较弱的尾部相依指数。
===
Ledford 和_Tawn(1996)_尾部相关系数
描述尾部相依性的另一种方法可以在Ledford & Tawn(1996)中找到。假设和具有相同的分布。现在,如果我们假设这些变量是(严格)独立的。
但如果我们假设这些变量是(严格的)同单调性的(即这里的变量是相等的,因为它们有相同的分布),则
所以,有这样一个假设:
那么a=2可以解释为独立性,而a=1则表示强(完美)正相依性。因此,考虑进行如下变换,得到[0,1]中的一个参数,其相依性强度随指数的增加而增加,例如
为了推导出尾部相依指数,假设存在一个极限,即
这将被解释为一个(弱)尾部相依指数。因此定义函数
下尾巴(在左边)
上尾(在右边)。计算这些函数的R代码非常简单。
> L2emp=function(z) 2*log(mean(U<=z))/ > R2emp=function(z) 2*log(mean(U>=1-z))/ + log(mean((U>=1-z)&(V>=1-z)))-1 > plot(c(u,u+.5-u\[1\]),c(L,R),type="l",ylim=0:1, > abline(v=.5,col="grey")
高斯copula函数
同样,也可以将这些经验函数与一些参数函数进行对比,例如,从高斯copula函数中得到的函数(具有相同的Kendall's tau)。
> copgauss=normalCopula(paramgauss) > Lgs =function(z) 2*log(z)/log(pCopula(c(z,z), + copgauss))-1 > Rgas =function(z) 2\*log(1-z)/log(1-2\*z+ + pCopula(c(z,z),copgauss))-1 > lines(c(u,u+.5-u\[1\])
Gumbel copula
> copgumbel=gumbelCopula(paramgumbel, dim = 2) > L=function(z) 2*log(z)/log(pCopula(c(z,z), + copgumbel))-1 > R=function(z) 2\*log(1-z)/log(1-2\*z+ + pCopula(c(z,z),copgumbel))-1 > lines(c(u,u+.5-u\[1\]),c(Lgl,Rgl),col="blue")
同样,我们观察置信区间,Gumbel copula在这里提供了一个很好的拟合
极值copula
我们考虑copulas族中的极值copulas。在双变量的情况下,极值可以写为
其中 为Pickands相依函数,它是一个凸函数,满足于
观察到,在这种情况下:
其中 肯德尔系数,可写成
例如
那么,我们就得到了Gumbel copula。现在,我们来看(非参数)推理,更准确地说,是相依函数的估计。最标准的估计器的出发点是观察 是否有copula函数
具有分布函数
而反过来,Pickands相依函数可以写成
因此,Pickands函数的自然估计是
其中, 是经验累积分布函数
这是Capéràa, Fougères & Genest (1997)中提出的估计方法。在这里,我们可以用
> Z=log(U\[,1\])/log(U\[,1\]*U\[,2\]) > h=function(t) mean(Z<=t) > a=function(t){ function(t) (H(t)-t)/(t*(1-t)) + return(exp(integrate(f,lower=0,upper=t, + subdivisions=10000)$value)) > plot(c(0,u,1),c(1,A(u),1),type="l"
整合得到Pickands相依函数的估计值。上图中可以直观地看到上尾的相依指数。
> A(.5)/2 [1] 0.405