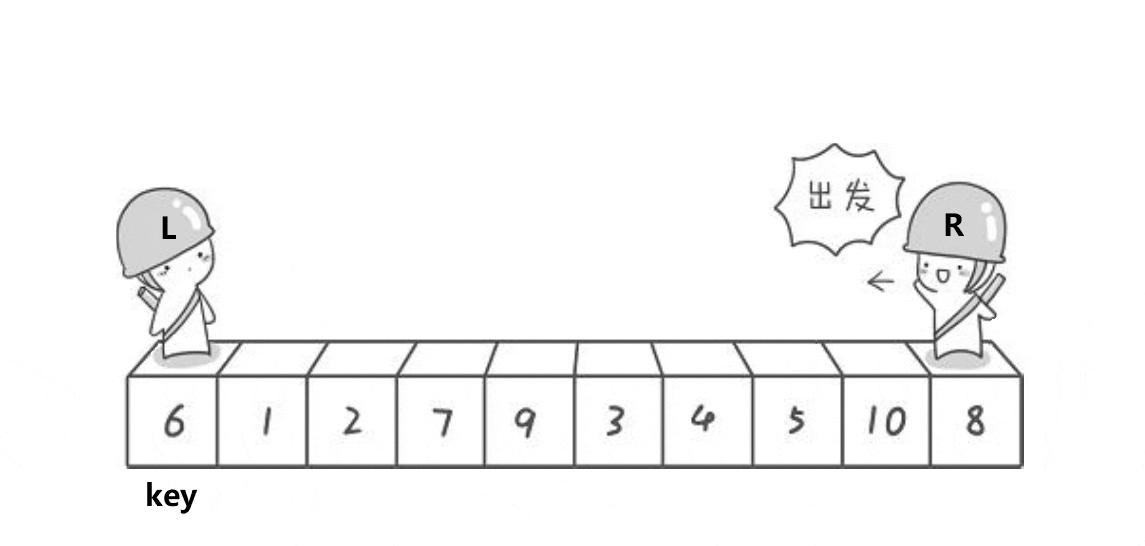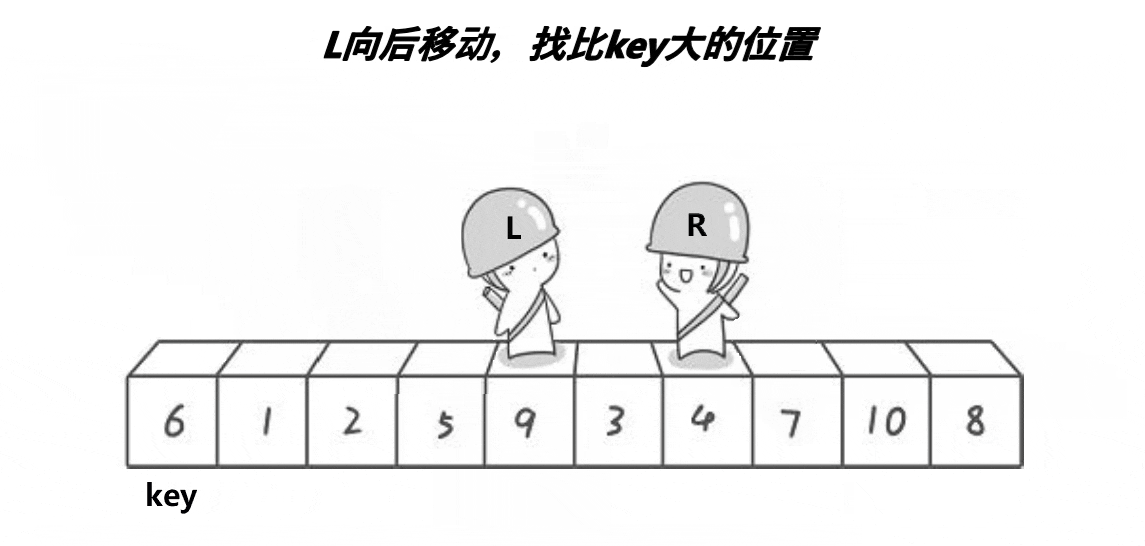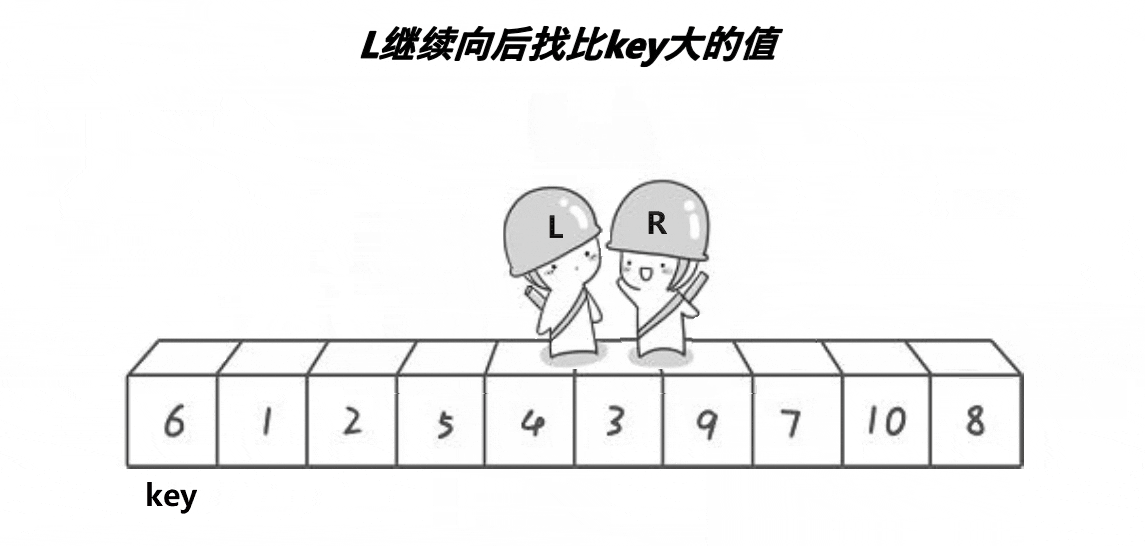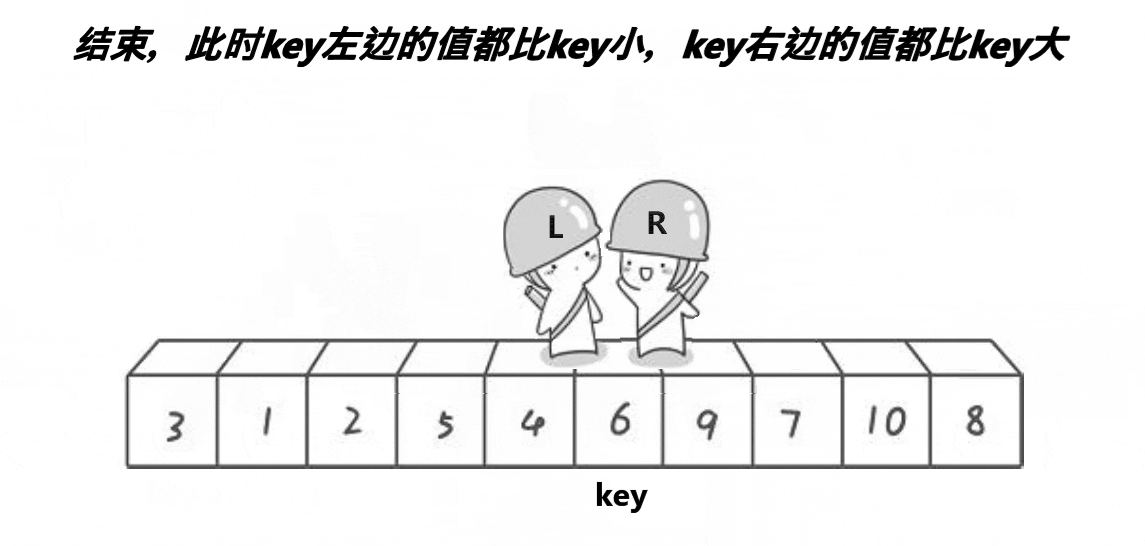
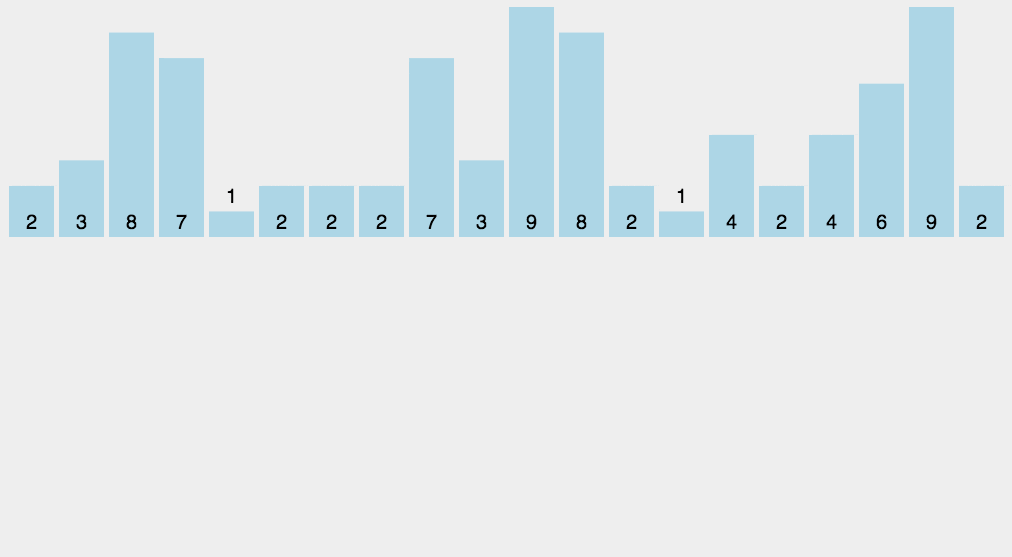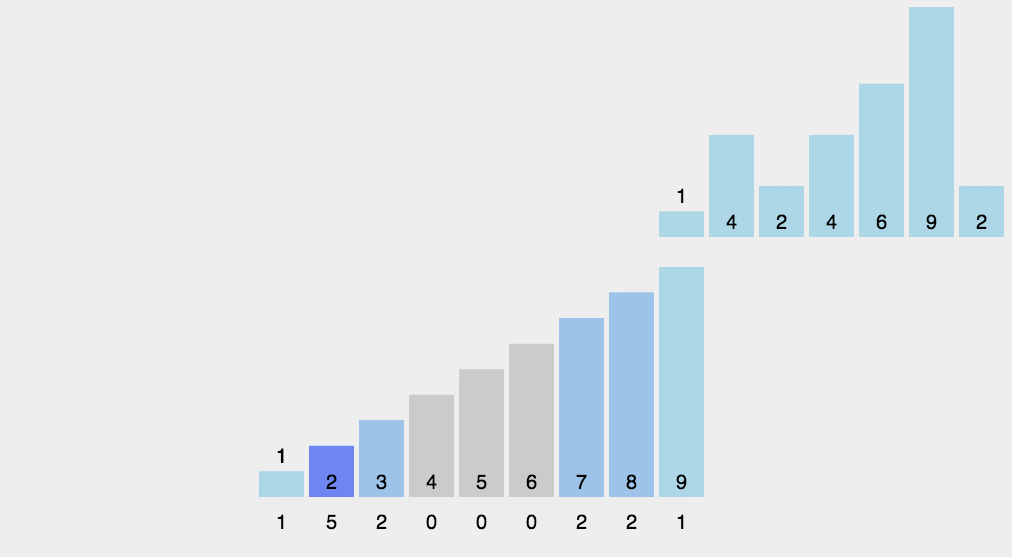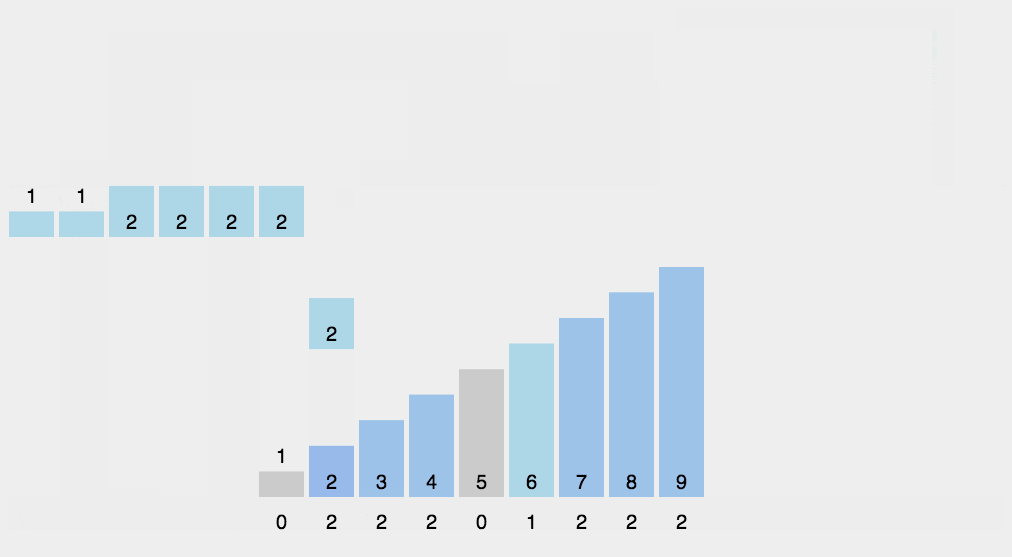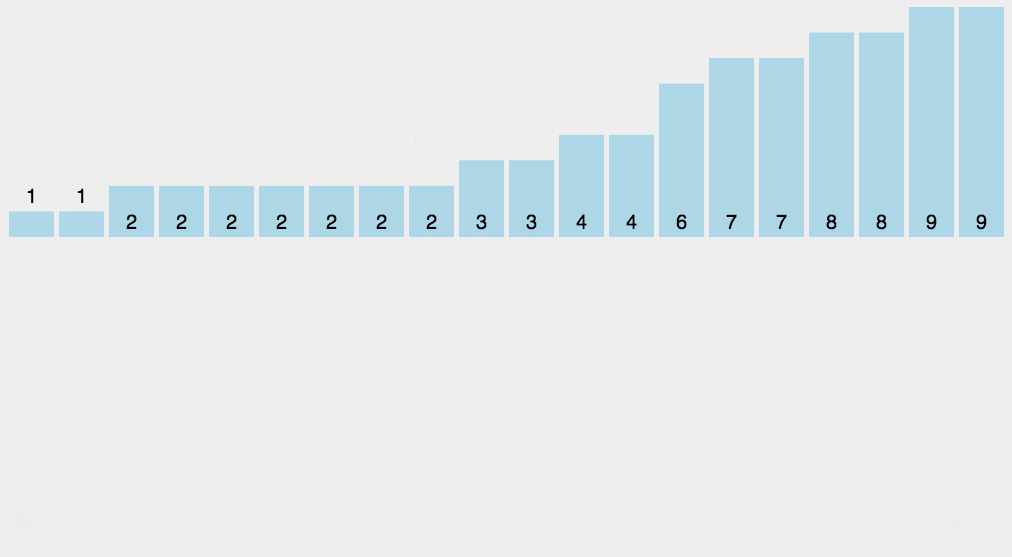1.递归写法
①三位取中函数
代码如下:
int GetMidIndex(int* a, int left, int right) { int mid = left + ((right - left) >> 1); if (a[left] < a[mid]) { if (a[mid] < a[right]) { return mid; } else if (a[left] > a[right]) { return left; } else { return right; } } else { if (a[mid] > a[right]) { return mid; } else if (a[left] < a[right]) { return left; } else { return right; } } }
三位取中的目的是为了防止面对有序最坏情况,变成选中位数做key,变成最好情况。
②hoare版本
代码如下:
int Partion1(int* a, int left, int right) { int mini = GetMidIndex(a, left, right); Swap(&a[mini], &a[left]); int keyi = left; while (left < right) { // 右边先走,找小 while (left < right && a[right] >= a[keyi]) --right; //左边再走,找大 while (left < right && a[left] <= a[keyi]) ++left; Swap(&a[left], &a[right]); } Swap(&a[left], &a[keyi]); return left; }
这里的主体思路是先指定首元素为key,先从数组尾部开始与key值比大小,直到找到比key小的元素再从左开始找比key大的元素,依次递归进行交换,直到left和right指针相遇中止,最后将key值与中间值交换,完成快排第一轮,再进入循环将中间值两边的值再操作,最终完成排序。需要注意的是,这里的三种写法都进行了三位取中优化。
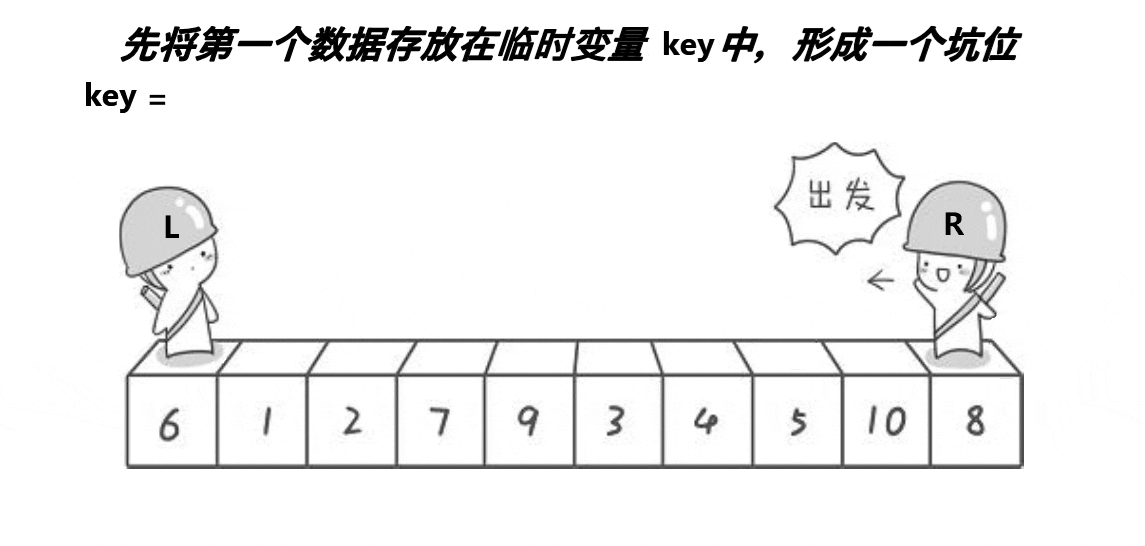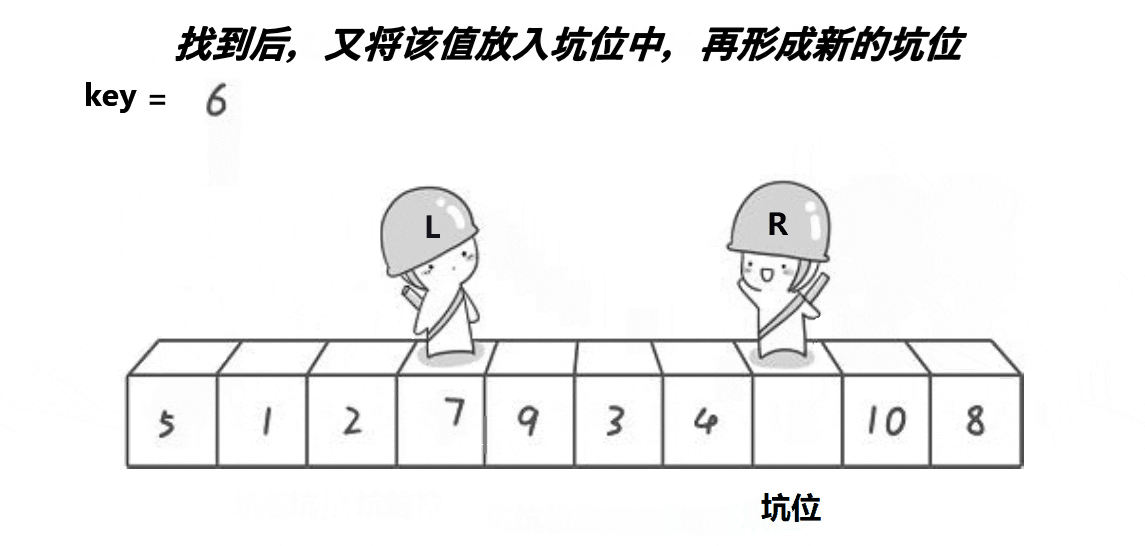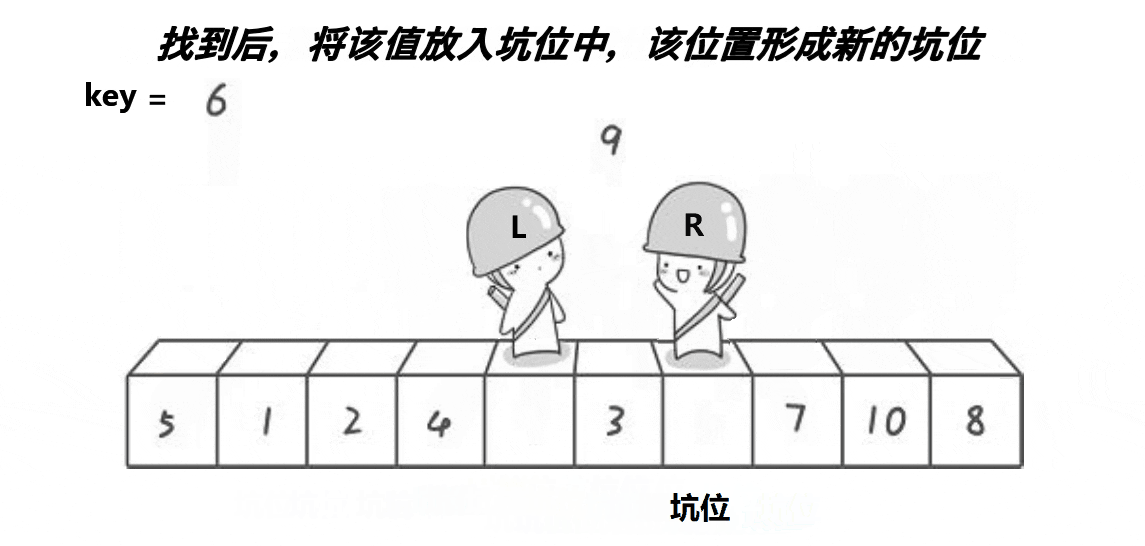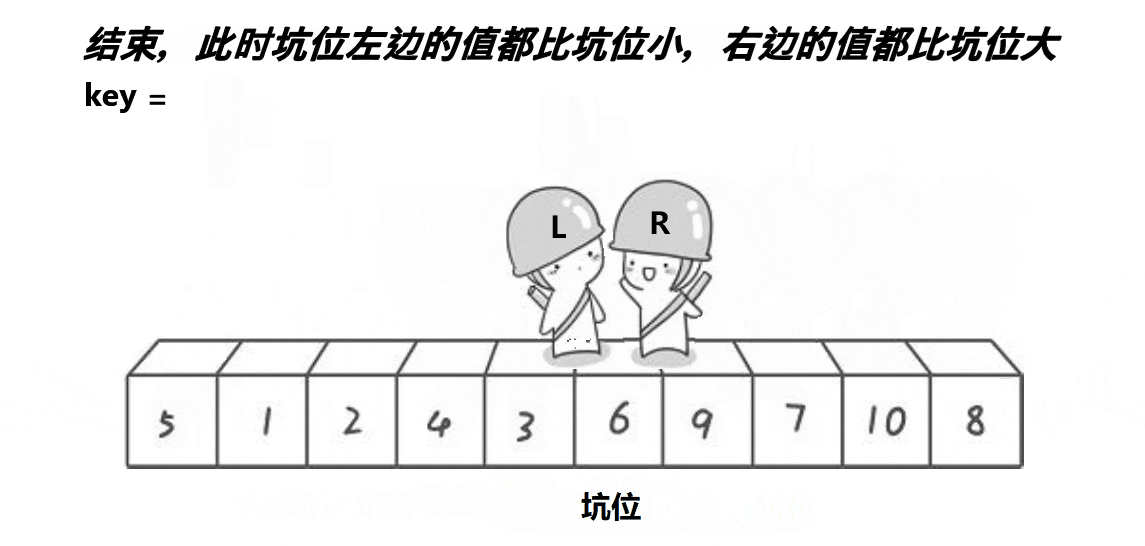
③挖坑法
代码如下:
int Partion2(int* a, int left, int right) { int mini = GetMidIndex(a, left, right); Swap(&a[mini], &a[left]); int key = a[left]; int pivot = left; while (left < right) { // 右边找小, 放到左边的坑里面 while (left < right && a[right] >= key) { --right; } a[pivot] = a[right]; pivot = right; // 左边找大,放到右边的坑里面 while (left < right && a[left] <= key) { ++left; } a[pivot] = a[left]; pivot = left; } a[pivot] = key; return pivot; }
该思路是先将首位元素赋给key值,将首元素位置指定为坑位,同样是从右边开始进行比大小,找到比key值小,将该值赋给首元素位置(即坑位),此元素初始位置设为新坑位,再从左边找比key大的值,找到后放进右边坑位,以此往复,最后留下的坑位填补为key存放的值,最后的递归步骤同上。
④前后指针版本
代码如下:
int Partion3(int* a, int left, int right) { int mini = GetMidIndex(a, left, right); Swap(&a[mini], &a[left]); int keyi = left; int prev = left; int cur = prev + 1; while (cur <= right) { if (a[cur] < a[keyi] && ++prev != cur) { Swap(&a[cur], &a[prev]); } ++cur; } Swap(&a[prev], &a[keyi]); return prev; }
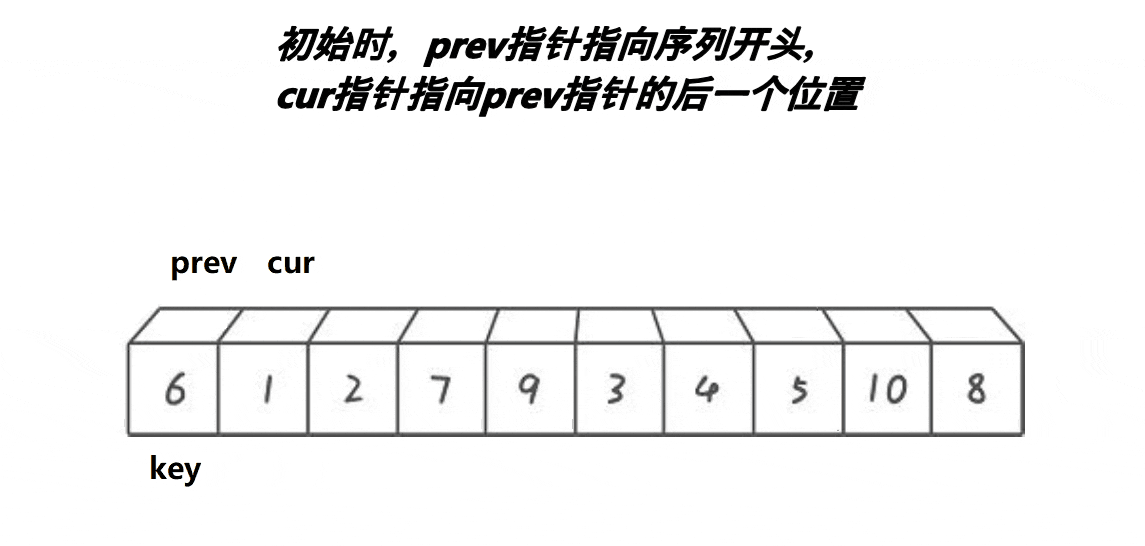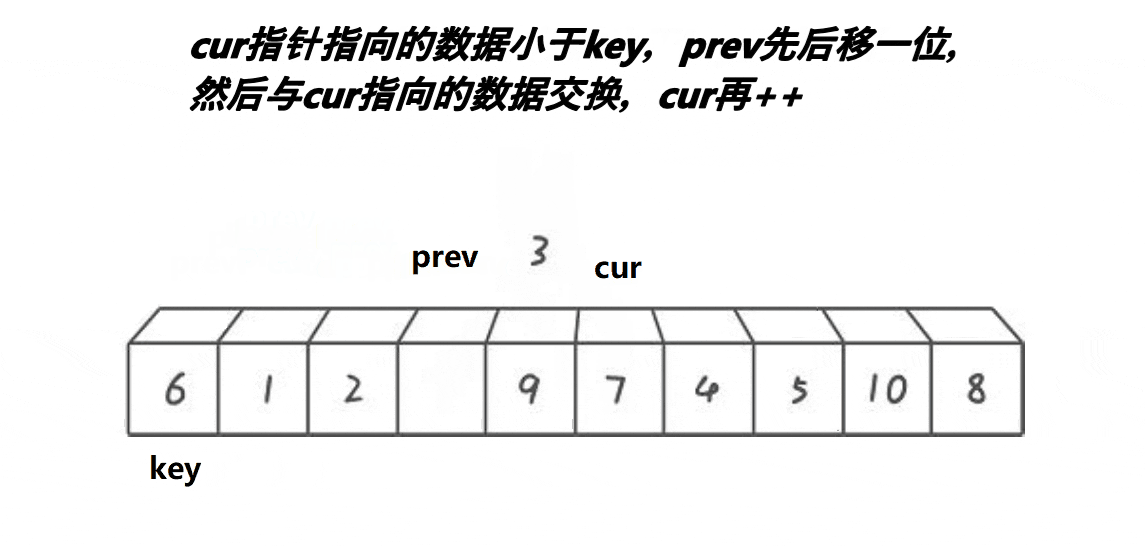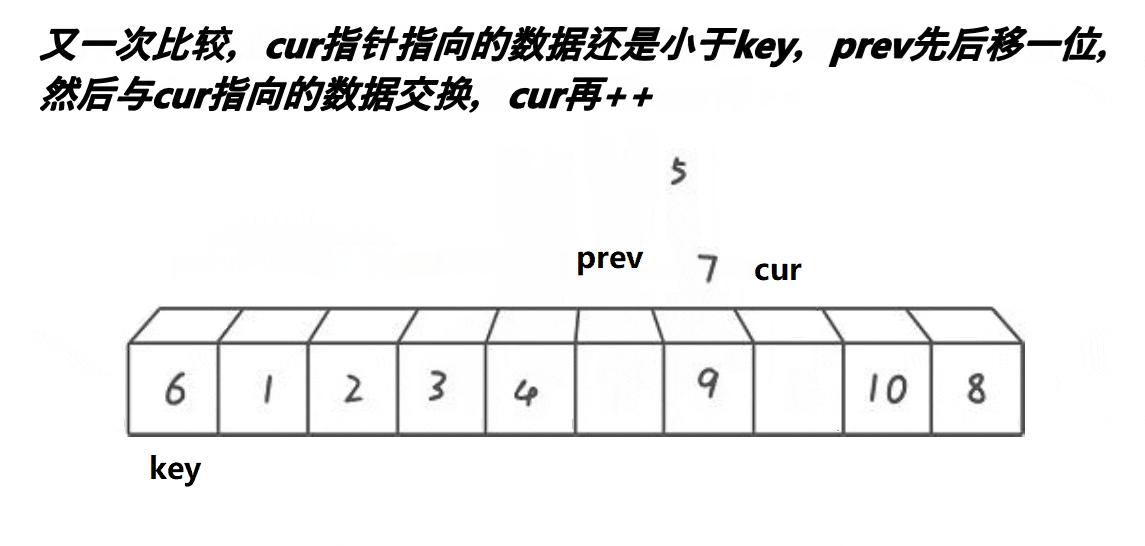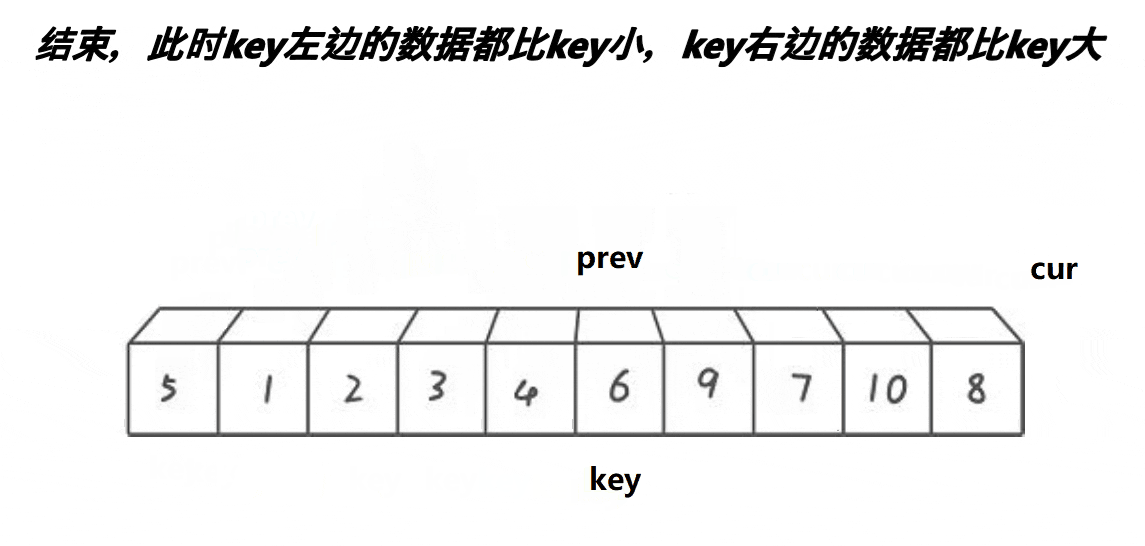
此算法的基本思路为:先指定第一个元素为key值,再指定cur与prev两个指针,prev指针指向第一个元素,cur指针指向第二个元素,cur指针先走找到比key小的元素停止,prev再向前走,找到比key大的元素停止,prev与cur的值进行交换,cur指针继续向前寻找比key小的值,以此递归,直到cur指针越界停止循环,将首元素值与此时的prev指向的值进行交换,key此时为枢轴,后递归同上。
⑥快排主函数
void QuickSort(int* a, int left, int right) { if (left >= right) return; { int keyi = Partion1(a, left, right); //int keyi = Partion2(a, left, right); //int keyi = Partion3(a, left, right); QuickSort(a, left, keyi - 1); QuickSort(a, keyi + 1, right); } }
递归程序的缺陷:
1.针对早期编译器相比循环程序,性能差;
2.递归深度太深,会导致栈溢出。(比如数组中都是相同数字的情况下)。
2.非递归写法
非递归写法是利用了栈,在C语言中,栈是需要自己写代码实现的,这里我套用的是之前写的关于栈的博客代码:
代码如下:
void QuickSortNonR(int* a, int left, int right) { ST st; StackInit(&st); StackPush(&st, left); StackPush(&st, right); while (!StackEmpty(&st)) { int end = StackTop(&st); StackPop(&st); int begin = StackTop(&st); StackPop(&st); int keyi = Partion3(a, begin, end); if (keyi + 1 < end) { StackPush(&st, keyi+1); StackPush(&st, end); } if (begin < keyi-1) { StackPush(&st, begin); StackPush(&st, keyi-1); } } StackDestroy(&st); }
快速排序的特性总结:
1.快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
2.时间复杂度:O(N*logN)
3.空间复杂度:O(logN)
4.稳定性:不稳定
七、归并排序
归并排序基本思想:
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and
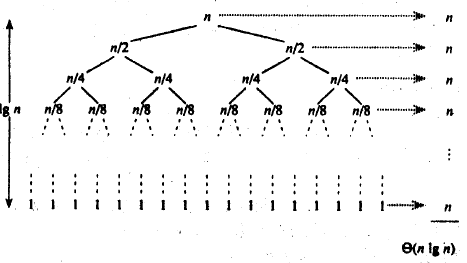
Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
1.递归写法
代码如下:
void _MergeSort(int* a, int left, int right, int* tmp) { if (left >= right) { return; } int mid = (left + right) / 2; _MergeSort(a, left, mid, tmp); _MergeSort(a, mid + 1, right, tmp); int begin1 = left, end1 = mid; int begin2 = mid+1, end2 = right; int i = left; while (begin1 <= end1 && begin2 <= end2) { if (a[begin1] < a[begin2]) { tmp[i++] = a[begin1++]; } else { tmp[i++] = a[begin2++]; } } while (begin1 <= end1) { tmp[i++] = a[begin1++]; } while (begin2 <= end2) { tmp[i++] = a[begin2++]; } for (int j = left; j <= right; ++j) { a[j] = tmp[j]; } } void MergeSort(int* a, int n) { int* tmp = (int*)malloc(sizeof(int)*n); if (tmp == NULL) { printf("malloc fail\n"); exit(-1); } _MergeSort(a, 0, n - 1, tmp); free(tmp); tmp = NULL; }
2.非递归写法
代码如下:
void MergeSortNonR(int* a, int n) { int* tmp = (int*)malloc(sizeof(int)*n); if (tmp == NULL) { printf("malloc fail\n"); exit(-1); } int gap = 1; while (gap < n) { for (int i = 0; i < n; i += 2 * gap) { int begin1 = i, end1 = i + gap - 1; int begin2 = i + gap, end2 = i + 2 * gap - 1; if (end1 >= n || begin2 >= n) { break; } // end2 越界,需要归并,修正end2 if (end2 >= n) { end2 = n- 1; } int index = i; while (begin1 <= end1 && begin2 <= end2) { if (a[begin1] < a[begin2]) { tmp[index++] = a[begin1++]; } else { tmp[index++] = a[begin2++]; } } while (begin1 <= end1) { tmp[index++] = a[begin1++]; } while (begin2 <= end2) { tmp[index++] = a[begin2++]; } // 把归并小区间拷贝回原数组 for (int j = i; j <= end2; ++j) { a[j] = tmp[j]; } } gap *= 2; } free(tmp); tmp = NULL; }
归并排序的特性总结:
1.归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
2.时间复杂度:O(N*logN)
3.空间复杂度:O(N)
4.稳定性:稳定
八、非比较排序
思想:计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。 操作步骤:
1.统计相同元素出现次数
2.根据统计的结果将序列回收到原来的序列中
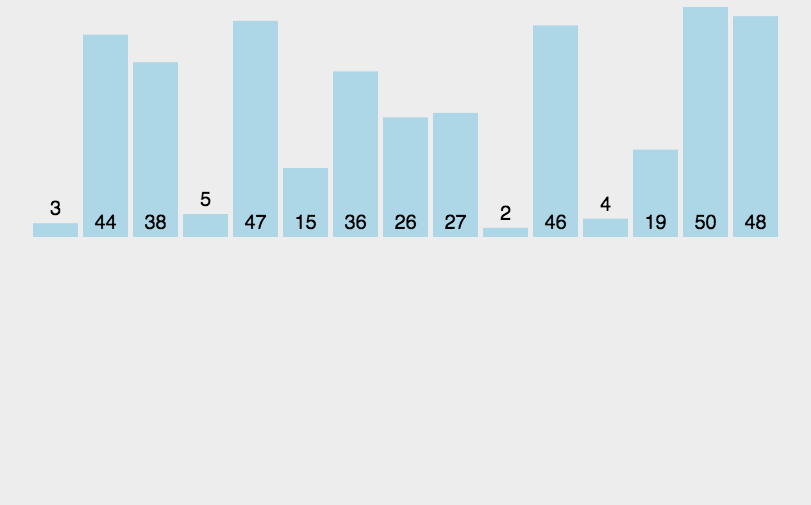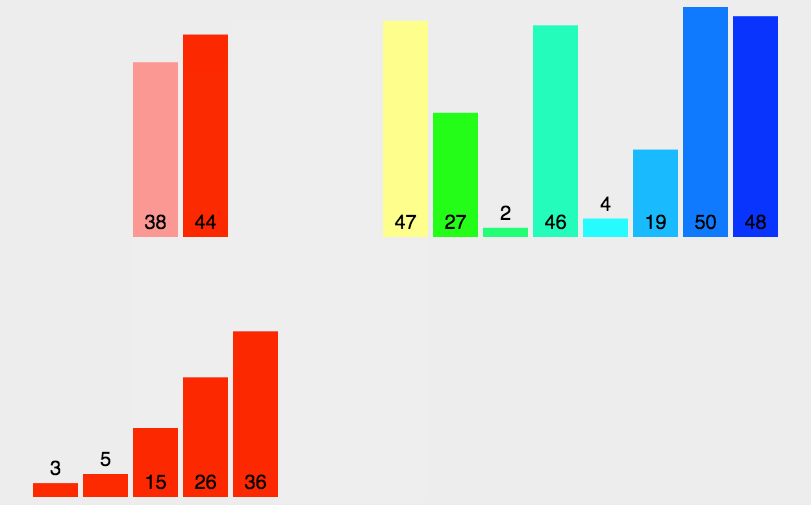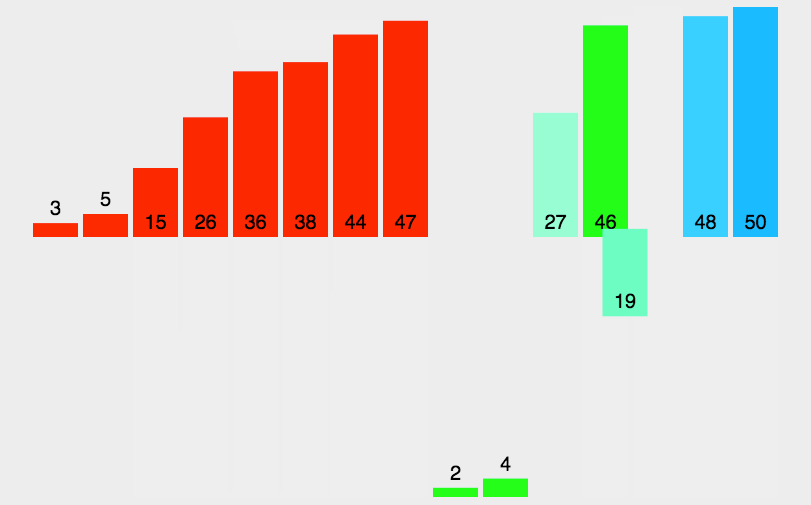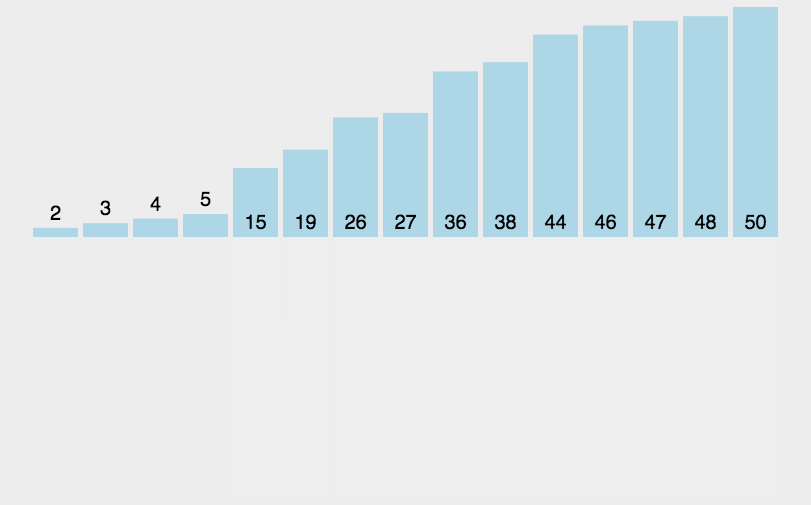
1.基数排序
基数排序的思路由最大值的位数与基数的定义,比如这里我们是给数组排序,最大位数为3,将0-9定为基数,则基数是10,拿(278,109,63,930,589,184,505,269,8,83)这个数组来讲,排序过程如下图,首先从数组从左至右个位开始,0-9依次插入相应位置,再从0-9依次取出,需要注意的是,先取先放进去的,在进行十位排序,过程同上,后同理。
最后排序结果为(8,63,83,109,184,269,278,505,589,930)
这里采用的是C++的写法,方便调用队列,想用C语言写的小伙伴可以参考博主之前关于队列的博客,进行调用修改,步骤相差无几。
代码如下:
#define _CRT_SECURE_NO_WARNINGS 1 #include<iostream> #include<stdio.h> #include<queue> using namespace std; #define K 3 #define RADIX 10 //定义基数 queue<int>Q[RADIX]; int GetKey(int value, int k) { int key = 0; while (k >= 0) { key = value % 10; value /= 10; k--; } return key; } void Distribute(int arr[], int left, int right, int k) { for (int i = left; i < right; ++i) { int key = GetKey(arr[i], k); Q[key].push(arr[i]); } } void Collect(int arr[]) { int k = 0; for (int i = 0; i < RADIX; ++i) { while (!Q[i].empty()) { arr[k++] = Q[i].front(); Q[i].pop(); } } } void RadixSort(int arr[], int left, int right)//[left,right) { for (int i = 0; i < K; ++i) { //分发数据 Distribute(arr, left, right, i); //回收数据 Collect(arr); } }
基数排序的特性总结:
1.时间复杂度:O(关键字位数d*n)
2.空间复杂度:O(关键字位数d*n)
3.稳定性:稳定
2.计数排序
计数排序的思路是基于基数排序的一种变形,我们先参考下图,假定数组值范围为1-9,基数为绝对映射,思路同基数排序,如果是某个范围内,则为相对映射,基数起始值为数组最小值,最终值为最大值。
代码如下:
void CountSort(int* a, int n) { int max = a[0], min = a[0]; for (int i = 1; i < n; ++i) { if (a[i] > max) { max = a[i]; } if (a[i] < min) { min = a[i]; } } int range = max - min + 1; int* count = (int*)malloc(sizeof(int)*range); memset(count, 0, sizeof(int)*range); if (count == NULL) { printf("malloc fail\n"); exit(-1); } for (int i = 0; i < n; ++i) { count[a[i] - min]++; } int j = 0; for (int i = 0; i < range; ++i) { while (count[i]--) { a[j++] = i + min; } } }
计数排序的特性总结:
1.计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。
2.时间复杂度:O(MAX(N,范围d))
3.空间复杂度:O(范围d)
4.稳定性:稳定
排序算法复杂度及稳定性分析
| 排序方法 | 平均情况 | 最好情况 | 最坏情况 | 辅助空间 | 稳定性 |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 |
| 希尔排序 | O(nlogn)~O(n^2) | O(n^1.3) | O(n^2) | O(1) | 不稳定 |
| 插入排序 | O(n^2) | O(n) | O(n^2) | O(1) | 稳定 |
| 冒泡排序 | O(n^2) | O(n) | O(n^2) | O(1) | 稳定 |
| 堆排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | 不稳定 |
| 快速排序 | O(nlogn) | O(nlogn) | O(n^2) | O(logn) | 不稳定 |
| 归并排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | 稳定 |
| 基数排序 | O(d*n) | O(d*n) | O(d*n) | O(n) | 稳定 |
| 计数排序 | O(d+n) | O(d+n) | O(d+n) | O(d) | 稳定 |
结语
有兴趣的小伙伴可以关注作者,如果觉得内容不错,请给个一键三连吧,蟹蟹你哟!!!
制作不易,如有不正之处敬请指出
感谢大家的来访,UU们的观看是我坚持下去的动力
在时间的催化剂下,让我们彼此都成为更优秀的人吧!!!