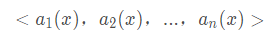谱聚类是一种基于图论的聚类方法,通过对样本数据的拉普拉斯矩阵的特征向量进行聚类,从而达到对样本数据聚类的目的。谱聚类可以理解为将高维空间的数据映射到低维,然后在低维空间用其它聚类算法(如KMeans)进行聚类
本文使用2021-2022年常规赛NBA球员的赛季数据。从特征之间的相关矩阵中绘制一个图表,显示可能相似的特征组,然后将研究谱聚类如何在这个数据集中工作。
数据中存在相关特征
在数据集进行EDA时,可能会得到一个结论:某些特征没有那么丰富的信息,一个简单的线性模型可以通过其他特征来准确预测它们。这种现象称为“多重共线性”,它不利于模型的泛化和可解释性。在理想情况下,我们希望特征都是彼此独立的,这样可以更好地解释和满足一些统计过程的假设,因为大多数统计模型假设随机变量是独立的。
我们可以用谱聚类算法对特征进行聚类来解决这个问题。
我们的数据集包括三张表:2021-2022赛季NBA球员的平均数据、高级数据和每百次控球数据。在球员姓名栏中加入特征后,我们计算特征的方差膨胀系数(VIF)来研究多重共线性。结果得到了下表:

因为合并了三个表,所以这些表中的一些特征彼此相关。
从相关矩阵创建图
为了能够看到相关的特征,我们画了一个特征图,将高度相关的特征连接在一起,希望能够找到公共相关性,循环相关性应该创建一些区域,其中每个特征依赖于其他特征。
# We only display correlations higher than 0.7 in absolute value
G=nx.Graph()
foriinrange(len(columns)):
col1=columns[i]
forjinrange(i):
col2=columns[j]
val=corr_matrix.values[i,j]
ifabs(val) >vis_threshold:
G.add_edge(columns.index(col1), columns.index(col2) , color=get_color(abs(val), color_threshold))
圆圈内的每一个整数都对应这个图中的一个特征。看看在图的右下角形成一个五边形的公共相关性,10-3323-3-4。
10:投篮命中率,33:进攻效率,23:真实命中率,3:有效投篮命中率。这几个都表示进攻的效率。
而中心的密集连接使我们无法手工选择所有的特征。所以需要一种数学方法来找到这些规律。
拉普拉斯特征图
首先需要为一对特征定义“链接”或“邻居”的概念。我们的目标是将上图分解为不相连的部分,其中每个部分都由成对相关的特征组成,不同的部分应尽可能独立。由于我们只显示高于 0.7 的相关性(绝对值,相关性也可以为负,这里不关心符号),因此使用以下邻接矩阵定义:

我们有D个特征,矩阵B是邻接矩阵。
而我们希望在K维空间中找到这些特征的表示形式,其中K是用户定义的数字,指定将使用多少个坐标来表示每个特征。拉普拉斯特征映射方法的目的是寻找特征的表示法,使相邻特征尽可能接近地表示。这是通过以下损失函数[1]来实现的。

y向量是K维特征的表示。E函数惩罚相邻表示之间的距离。我们与论文不同,将y按行而不是列堆叠,以便更容易地看到特征向量的坐标解释。D是数据中特征的数量。
通过显式地写出这个和的项,可以很容易地看到这个问题实际上是一个轨迹最小化问题。

对使用 D 矩阵缩放的 Y 施加正交约束,可以从与 K 个最小非零特征值相关联的归一化拉普拉斯算子的特征向量中获得此优化问题的解 Y [1]。

Y矩阵的初始定义是将表示叠加到行上,但这里我们将特征向量叠加到列上,表明每个特征向量为表示增加一个维度。
我们最初的目标是将邻接图切割成小块,其中每个小块是一组独立于其他小块的特征。
这里我们想用损失函数来模拟目标。所以假设有m个不相交的邻接图顶点子集,惩罚子集之间的交叉连接,也就是说,不希望一个子集中的顶点连接到另一个子集[1]中的顶点。

这里的F是符合目标的损失函数。分子在一个顶点的交叉连接上求和,用总的簇内连接归一化。这里可以将总和中的项解释为给定子集的交叉连接与内部连接的比率。不相交的子集实际上就是要寻找的特征的谱簇。
下一步就是要证明拉普拉斯特征映射误差F和E之间的相似性。对于特征(上面定义的V集)的给定划分(聚类),定义一个矩阵Z,其形状为(D, m)。

该矩阵的列表示簇的元素。为了更清楚地说明这一点,这里演示了当D = 4和m = 3时这个矩阵是怎样的

上图有问题,只是为了演示
函数F是

这里的L是上面定义的拉普拉斯矩阵。与拉普拉斯特征映射的轨迹恒等式相同,但约束条件不同。
这样,我们将找到簇的问题变为找到一个最小化这条轨迹的上述形式的矩阵 Z。尽管有相似性,但这与拉普拉斯特征图不是同一个问题,因为 Z 的选择仅限于上述形式。如果不局限于这种形式,则Z的列一定是前m个特征向量。
为了放宽此约束并使用拉普拉斯特征图的机制,并且观察到 Z 矩阵的每一行都分配给一个簇,这与拉普拉斯特征映射类似,所以可以用Y矩阵代替Z, Y矩阵的行是K维特征的表示。所以要使用这两个最小化问题之间的联系,Z可以被认为是Y行的聚类版本。为了简化问题,只要设置Z等于与前m个非零最小特征值相关的前m个特征向量的堆栈,然后将其行聚类。
聚类步骤
取拉普拉斯算子的前 7 个特征向量来构造 Z,并采用分层聚类方法寻找Z行内的聚类。

我们检查树图,决定设置n_cluster = 6。这些特征簇是:

这6个组都有有意义的解释。
- 第一个有点复杂,因为图的中心有一个非常密集的区域但是可以看到投篮次数、罚球次数、PER、使用率和场均时间统计数据被收集在这里,其他数据随着球员上场时间和进攻责任的增加而增加。因此可以得出结论,这个簇对应于进攻活动。
- 第二个是组织能力,因为持球者通常有更高的失误。
- 第三个对应进攻效率。
- 第四个只有一个特征,表示球员的防守技巧
- 第五个是篮板能力。
- 最后一个是球员的三分球技术。
这里一个很好的发现是,我们的方法成功地区分了篮板和防守技能。好的篮板手并不总是好的防守(篮板包含进攻和防守,而防守不仅仅只有篮板),但是他们之间可能存在相关性。
该方法可以说的确成功地找到了邻接图的分组
总结
本文中我们绘制了特征的邻接图,展示了如何通过拉普拉斯矩阵的行发现特征之间的公共相关性,并进行聚类。
本文的代码:
https://avoid.overfit.cn/post/cfaa81824c714736970e7f49ffde07ab
作者:Yiğithan Gediz