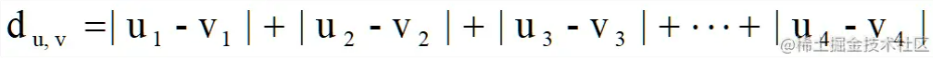明可夫斯基距离(闵氏距离)Minkowski
Minkowski距离比大多数距离更复杂。它是在范数向量空间(n维实数空间)中使用的度量,这意味着它可以在任何距离可以表示为具有长度的向量的空间中使用。
该措施具有三个要求:
- 零向量—零向量的长度为零,而每个其他向量的长度为正。例如,如果我们从一个地方到另一个地方旅行,那么该距离始终为正。但是,如果我们从一个地方到自己的地方旅行,则该距离为零。
- 标量因数—当向量与正数相乘时,其长度会更改,同时保持其方向。例如,如果我们在一个方向上走了一定距离并添加了相同的距离,则方向不会改变。
- 三角形不等式—两点之间的最短距离是一条直线。
Minkowski距离的公式如下所示:
关于这个距离度量最有趣的是参数p的使用。我们可以使用这个参数来操纵距离度量,使其与其他度量非常相似。
常见的p值有:
p=1 -曼哈顿距离
p=2 -欧氏距离
p=∞- 切比雪夫距离
缺点
Minkowski与它们所代表的距离度量具有相同的缺点,因此,良好地理解曼哈顿距离、欧几里得距离和切比雪夫距离等度量标准是非常重要的。
此外,使用参数p实际上可能很麻烦,因为根据您的用例,查找正确的值在计算上可能非常低效。
用例
p的好处是可以迭代它,并找到最适合用例的距离度量。它允许您在距离度量上有很大的灵活性,如果您非常熟悉p和许多距离度量,这将是一个巨大的好处。
Jaccard指数
Jaccard指数(交并比IOU)是一个用于计算样本集的相似性和多样性的度量。它是交集的大小除以样本集的并集的大小。
实际上,它是集合之间相似实体的总数除以实体的总数。例如,如果两个集合有1个共同的实体,而总共有5个不同的实体,那么Jaccard索引将是1/5 = 0.2。
要计算Jaccard距离,我们只需从1中减去Jaccard指数:
缺点
Jaccard指数的主要缺点是它受到数据大小的很大影响。大型数据集可能会对指数产生很大影响,因为数据量大的话可能显著增加并集,同时保持交集不变。
用例
Jaccard索引通常用于使用二进制或二进制数据的应用程序中。当您拥有一个预测图像片段(例如汽车)的深度学习模型时,可以使用Jaccard索引来计算给定真实标签的预测片段的准确性。
同样,它也可以用于文本相似度分析,以衡量文档之间的选词重叠程度。因此,它可以用来比较模式集。
半正矢距离(haversine)
Haversine距离是指球面上两个点之间的经度和纬度。它与欧几里得距离非常相似,因为它可以计算两点之间的最短线。主要区别在于不可能有直线,因为这里的假设是两个点都在一个球面上。
缺点
这种距离测量的一个缺点是,假定这些点位于一个球体上。实际上,这种情况很少出现,例如,地球不是完美的圆形,在某些情况下可能会使计算变得困难。取而代之的是,将目光转向假定椭圆形的Vincenty距离。
用例
如您所料,Haversine距离通常用于导航。例如,您可以使用它来计算两个国家之间的飞行距离。请注意,如果距离本身不那么大,则不太适合。曲率不会产生太大的影响。
Sørensen-Dice 指数
Sørensen-Dice指数与Jaccard指数非常相似,它衡量的是样本集的相似性和多样性。尽管它们的计算方法类似,但Sørensen-Dice索引更直观一些,因为它可以被视为两个集合之间重叠的百分比,这是一个介于0和1之间的值。
这个指数在距离度量中很重要,因为它允许更好地使用没有v的度量
DICE指数是一个用于计算样本集的相似性和多样性的度量。它是交集的大小除以样本集的并集的大小。
实际上,它是集合之间相似实体的总数除以实体的总数。例如,如果两个集合有一个共同的实体,而总共有5个不同的实体,那么DICE指数将是1/5 = 0.2。
缺点
就像Jaccard指数一样,它们都夸大了很少或没有真值的集合。它可以控制多组平均得分并按相关集合的大小成反比地加权每个项目,而不是平等对待它们。
用例
用例与Jaccard指数相似。您会发现它通常用于图像分割任务或文本相似性分析中。
注意:比这里提到的9种距离测量更多。如果您正在寻找更有趣的指标,我建议您研究以下内容之一:Mahalanobis, Canberra, Braycurtis, and KL-divergence.