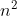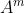1.邻接矩阵
1.1.邻接矩阵的定义
采用一维数组存放顶点数据,二维数组存放边的数据(各顶点是否邻接)
- 无向图:A[i][j] = 0,则图中Vi和Vj不邻接;A[i][j] = 1,则图中Vi和Vj邻接
- 有向图:A[i][j] = 0,则图中没有Vi指向Vj的边;A[i][j] = 1,则图中有Vi指向Vj的边
#define MAXVERTEXNUM 100 //顶点数最大值为100 typedef struct MGraph{ char Vex[MAXVERTEXNUM]; //一维数组,存放顶点数据 int Edge[MAXVERTEXNUM][MAXVERTEXNUM]; //二维数组,存放邻接矩阵 int verNum, arcNum; //顶点数,弧数 }MGraph;
1.2.求度、入度和出度
- 度:第 i 行或者第 i 列的非0元素的个数
- 入度:第 i 列非0元素的个数
- 出度:第 i 行非0元素的个数
1.3.邻接矩阵的性能
- 空间复杂度O()(二维数组 顶点数*顶点数)
- 适合存储稠密图
- 如果是无向图,可以只存储上三角或者下三角(特殊矩阵的压缩)
1.4.邻接矩阵的性质
设图G的邻接矩阵为A,的元素[i][j]等于由顶点 i 到顶点 j 的长度为 n 的路径数目
2.邻接表法
2.1.邻接表的定义
邻接表为图中每个顶点都建立一个单链表,该表中存放该顶点的所有邻接结点,并成为边表;而边表的头指针和顶点的数据信息采用顺序存储,称为顶点表
其中firstarc指向该顶点的第一个邻边,nextarc指向该顶点的下一个邻边
#define MAXVERTEXNUM 100 //最大顶点数 typedef struct ArcNode{ //边表结点 int adjevex; //该弧指向的顶点的数组下标 struct ArcNode *next; //指向下一条弧的指针 //InfoType info; //网的边权值 }ArcNode; typedef struct VNode{ //顶点表结点 VertexType data; //顶点信息 ArcNode *first; //指向第一条邻边的指针 }VNode, AdjList[MAXVERTEXNUM]; typedef struct{ AdjList vertices; //邻接表 int vexNum, arcNum; //顶点数和弧数 }ALGraph;
2.2.邻接表的空间复杂度
无向图中,每一条边都被保存了两次,因此空间复杂度为O(|V| + 2|E|)
有向图中,每一条边只被保存了一次,因此空间复杂度为O(|V| + |E|)
2.3.邻接表的度、入度和出度
度:遍历该顶点的边表,有几个则度就为几
出度:遍历该顶点的边表,有几个则出度就为几
入度:遍历除该顶点外的其他所有顶点边表,共有几个指向该顶点的弧,则入度就为几
2.4.邻接表与邻接矩阵的不同点
邻接矩阵:稠密图;确定顶点编号则图唯一
邻接表:稀疏图;图不唯一
3.十字链表(有向图)
十字链表弥补了邻接表查找入度困难的缺点,它既容易查找顶点的入度,也容易找顶点的出度
顶点结点的data域存放数据,firstin域存放第一个指向它的弧的指针,firstout域存放第一个指出的指针
弧结点的tailvex域存放弧尾的顶点,haedvex域存放弧头的顶点,hlink域存放下一个弧头和该顶点相同的弧的指针,tlink域存放下一个弧尾和该顶点相同的弧的指针
找入度:从该顶点结点的firstin开始找,再进入弧结点的hlink
找出度:从该顶点结点的firstout开始找,再进入弧结点的tlink
4.邻接多重表(无向图)
邻接表存放无向图时,每条边会存放两次,浪费大量空间,因此,采用邻接多重表
邻接多重表的结构类似十字链表
顶点结点:data存放顶点结点的数据;firstedge存放第一条依附于该节点的边
5.图的基本操作
Adjacent(G, x, y); //判断图是否存在边<x, y>或者(x, y)
最好时间复杂度O(1):该顶点的下一个边结点即为要搜索的边
最坏时间复杂度O(|V|):该顶点的最后一个边界点是要搜索的边O(|V| - 1)
Neighbors(G, x); //列出图G与顶点x邻接的边
无向图:
- 最好时间复杂度O(1):该顶点只有一个边(邻接表)
- 最坏时间复杂度O(|V|):该顶点的边有V - 1条(邻接表);遍历整行n个顶点(邻接矩阵)
有向图:
- 最好时间复杂度O(1):出边:该顶点只有一个出边(邻接表)
- 最坏时间复杂度:遍历整行n个结点O(|V|)(邻接矩阵);入边:遍历全部边结点O(|E|)(邻接表)
InsertVertex(G, x); //在图中插入顶点x
时间复杂度为O(1):有向图、无向图、邻接矩阵、邻接表都一样(新顶点刚开始不连任何边)
DeleteVertex(G, x); //在图中删除顶点x
无向图:
- 最好时间复杂度O(1):该顶点没有相邻的边(邻接表)
- 最坏时间复杂度:删除该顶点的行和列O(|V|)(邻接矩阵);该顶点邻接了尽可能多的边,则需要遍历其他所有边O(|E|)(邻接表)
有向图:
- 邻接矩阵:删除行列O(|V|)
- 邻接表:
- 删出边:O(1)没有出边,O(|V|)
- 删入边:O(|E|)遍历所有边
AddEdge(G, x, y); //添加<x, y>或者(x, y)
邻接矩阵:O(1)顺序表随机存储特性
邻接表:O(1)头插法,O(|V|)尾插法
FirstNeighhbor(G, x); //求图G中顶点x的第一个邻接顶点
无向图:
- 邻接矩阵:遍历行,最好时间复杂度第一个O(1),最坏时间复杂度最后一个或不存在O(|V|)
- 邻接表:顶点结点连着的第一个边结点O(1)
有向图:
- 邻接矩阵:出边行,入边列 O(1) ~ O(n)
- 邻接表:
- 入边O(1),指定节点的第一个边结点
- 出边O(1),遍历所有边O(1) ~ O(|E|)
NextNeighbor(G, x, y); //顶点y是图G中顶点x的一个邻接点,返回除y外的下一个邻接点
6.王道课后题
1.无向图:邻接矩阵中遍历上三角或者下三角,统计有多少个非零元素;邻接表中遍历所有边结点,边的数量为边结点的一半
有向图:邻接矩阵种遍历所有行,统计有多少个非零元素;邻接表中遍历所有边结点,边的数量即为边结点数量
2.无向图:邻接矩阵中查找第 i 行 j 列是否为非零;邻接表中遍历 i 的顶点结点相连的边结点是否有指向j的边结点
有向图:邻接矩阵中查找第 i 行 j 列和第 j 行 i 列是否为非零;邻接表中分别遍历 i 和 j 的顶点结点相连的边结点
3.无向图:邻接矩阵中遍历行,非零元素的个数即为度;邻接表中遍历其相连的边结点,边结点个数即为度
有向图:邻接矩阵中出度遍历行,入度遍历列,非零元素个数即为度;邻接表中出度遍历该节点的边结点,边结点个数即为出度;入度需遍历全部边结点
#define MaxVertexNum 100 typedef struct ArcNode{ struct ArcNode *next; int adjvex; }ArcNode; typedef struct VNode{ elemtype data; ArcNode *first; }VNode, AdjList[MaxVertexNum]; typedef struct Grpah{ AdjList vertices; int vexNum, arcNum; }Graph void Convert(Graph &G, int arr[][]){ for (int i = 0; i < G.vexNum; i++){ //找到第一个结点 ArcNode *p = (G->vertices[i]).first; //循环遍历下一个结点 while(p){ //将第i行p->adjvex列置为1 arr[i][p->adjvex] = 1; p = p->next; } } }
int IsExitEl(MGraph G){ int degree; int n = 0; //遍历图的各个顶点 for (int i = 0; i < G.numVertices; i++){ //度清零 degree = 0; //二维数组的当前元素值不等于0,则度数+1 for (int j = 0; j < G.numVertices; j++) if (Edge[i][j]) degree++; //度数为奇数,则个数+1 if (degree % 2) n++; }//for //个数为0或者2,return 1;否则,return 0 if (n == 0 || n == 2) return 1; else return false; }