
一些同学对计算机运行的速度没有概念
可能就是感觉计算机运行速度应该会很快
但我们在做算法题目的时候为什么会超时呢?
我们的计算机究竟1s可以计算多少次呢?
接下来我们来探讨一下这几个问题。
超时是怎么回事

大家刷leetcode时候应该都遇到过知一种错误是超时
也就是说程序运行的时间超过了规定的时间,而leetcode并没说程序运行了多久超时,也没有说超时时间具体是多少
一般现在判题系统的超时时间就是1s,其他OJ呢,例如POJ 或者ZOJ 超时时间都基本上都是1s
也就是用例数据输入后最多要1s内得到结果,leetcode 应该也是1s左右(leetcode上可能每道题限制会有所不同)。
下文为了方便讲解,暂定超时时间就是1s
接下来我们要知道我们的代码为什么会超时的
也就是如果我们写出了一个O(n)的算法 ,我们其实可以估算出来n是多大的时候,我们算法的执行之间就会超过1s
如果知道n的规模已经足够让O(n)的算法运行时间超过了1s,此时我们就应该考虑log(n)的解法
从硬件配置看计算机的性能
因为我们主要看计算机的运算速度,所以主要看CPU的配置
以我自己的Macpro为例 CPU配置:2.7 GHz Dual-Core Intel Core i5
也就是 2.7 GHz 奔腾双核,i5处理器
这里在介绍一下 GHz的概念
1Hz = 1/s
1Hz 就可以理解是cpu单位时间内完成了一次操作,我们称之为为赫兹
那么1GHz等于多少赫兹呢
1GHz(吉赫)= 1000MHz(兆赫)
1MHz(兆赫)= 1百万赫兹
所以 1GHz = 10亿Hz,表示CPU可以一秒运行10亿次,2.7GHz就是27亿次
再加上双核所以就是理论上我的计算机1s可以运行54亿次
但是不要以为计算机的cpu 1s运行54亿运算都用到了我们自己写的程序上
这里面水分很多的,首先不是CPU每次运行都能实现一次运算,有时候大概运行十几次才能完成一次运算。
例如CPU执行一步完整的乘法,不仅涉及寄存器的调用,还多其他数据处理的操作。
同时cpu也要执行计算机的各种进程任务等等,我们的程序仅仅是其中的一个进程而已
所以我们的程序在计算机上究竟1s真正能执行多少次操作呢?
做个试验测一下计算机的运行速度
我们来测一下计算机的运行速度究竟是多少
这是我们需要的头文件
// 头文件
#include <iostream>
#include <chrono>
#include <thread>
using namespace std;
using namespace chrono;
我们实现三个函数,时间复杂度分别是 O(n) , O(n^2), O(nlogn)
// O(n)
void function1(long long n) {
long long k = 0;
for (long long i = 0; i < n; i++) {
k++;
}
}
// O(n^2)
void function2(long long n) {
long long k = 0;
for (long long i = 0; i < n; i++) {
for (long j = 0; j < n; j++) {
k++;
}
}
}
// O(nlogn)
void function3(long long n) {
long long k = 0;
for (long long i = 0; i < n; i++) {
for (long long j = 1; j < n; j = j*2) { // 注意这里j=1
k++;
}
}
}
那么接下来我们来看一下这三个函数随着n的规模变化,耗时会产生多大的变化
这里呢 假如我们先测function1 ,就把 function2 和 function3 注释掉
int main() {
long long n; // 数据规模
while (1) {
cout << "输入n:";
cin >> n;
milliseconds start_time = duration_cast<milliseconds >(
system_clock::now().time_since_epoch()
);
function1(n);
// function2(n);
// function3(n);
milliseconds end_time = duration_cast<milliseconds >(
system_clock::now().time_since_epoch()
);
cout << "耗时:" << milliseconds(end_time).count() - milliseconds(start_time).count()
<<" ms"<< endl;
}
}
我们来看一下运行的效果。
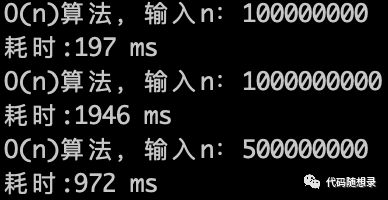
O(n)的算法,1s内大概计算机可以运行 5*(10^8)次计算
接下来我们来推测一下O(n^2) 的算法,1s 可以 运行多少次计算呢, 应该是对5*(10^8)开根号 的次数
看一下实验数据

O(n^2)的算法,1s内大概计算机可以运行 22500次计算, 验证了刚刚的推测
在推测一下O(nlogn)的话, 1s可以运行多少次呢,理论上应该是比 O(n)少一个数量级
因为logn的复杂度 其实是很快。
再看一下实验数据

O(nlogn)的算法,1s内大概计算机可以运行2*(10^7)次计算,符合我们的预期
完整的测试代码,可以在这里获取
https://github.com/youngyangyang04/algorithm_interview_course/blob/master/chapter_two/section_2.cpp
总结
这是在我自己的计算机上测出来的数据,不能说是十分精确,数量级是差不多的,大家可以用来参考一下

至于O(logn) 和O(n^3) 等等这些时间复杂度在1s内可以处理的多大的数据规模,同学们可以自己想一想写代码去测一下
通过这一篇文章希望大家对数据规模和超时错误 有一个初步的认识!
来源 | 代码随想录
作者 | 代码随想录
版权声明:本文内容由阿里云实名注册用户自发贡献,版权归原作者所有,阿里云开发者社区不拥有其著作权,亦不承担相应法律责任。具体规则请查看《阿里云开发者社区用户服务协议》和《阿里云开发者社区知识产权保护指引》。如果您发现本社区中有涉嫌抄袭的内容,填写侵权投诉表单进行举报,一经查实,本社区将立刻删除涉嫌侵权内容。