定义
一个PXP的有向图中,路径覆盖就是在图中找一些路径,使之覆盖了图中的所有顶点,且任何一个顶点有且只有一条路径与之关联;(如果把这些路径中的每条路径从它的起始点走到它的终点,那么恰好可以经过图中的每个顶点一次且仅一次);如果不考虑图中存在回路,那么每条路径就是一个弱连通子集.
由上面可以得出:
1.一个单独的顶点是一条路径;
2.如果存在一路径p1,p2,......pk,其中p1 为起点,pk为终点,那么在覆盖图中,顶点p1,p2,......pk不再与其它的顶点之间存在有向边.
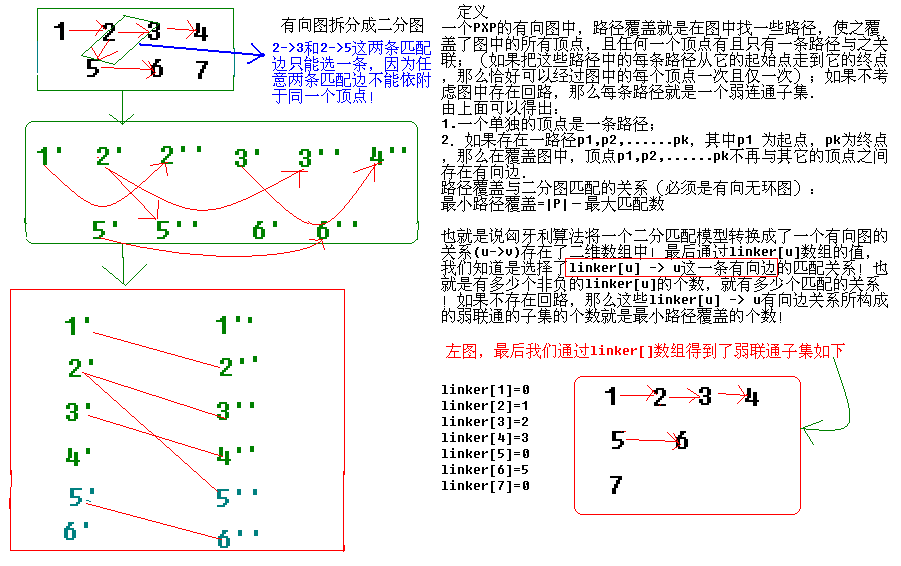
路径覆盖与二分图匹配的关系(必须是有向无环图):
最小路径覆盖=|P|-最大匹配数
也就是说匈牙利算法将一个二分匹配模型转换成了一个有向图的关系(u->v)存在了二维数组中!最后通过linker[u]数组的值,我们知道是选择了linker[u] -> u这一条有向边的匹配关系!也就是有多少个非负的linker[u]的个数,就有多少个匹配的关系!如果不存在回路,那么这些linker[u] -> u有向边关系所构成的弱联通的子集的个数就是最小路径覆盖的个数!
本文转自 小眼儿 博客园博客,原文链接:http://www.cnblogs.com/hujunzheng/p/3917855.html,如需转载请自行联系原作者