考虑支持插入,删除和查找操作的并发数据结构实现。如果这些操作只处理键值(译者注:而不处理具体值),这样的数据结构会是一个集合。如果一个数据值与每一个键关联起来,我们就得到了一部数据字典。由于他们都是密切相关的数据结构,一个并发的集合通常能够经过适当修改来实现一部字典。在接下来的三个小节中,我们将专注于利用linked lists,hash tables,和trees这三种不同的数据结构来实现集合。
试想我们使用一个linked list去实现集合。除了锁住整个linked list来避免并发操作以外,最普遍的实现基于锁的linked lists的方式是hand-over-hand-locking(有时也叫lock coupling)。在这种方式下,每个节点都有一个关联的锁。一个正在遍历Linked list的线程只有在获取到了下一个节点的锁时才会释放上一个节点的锁,这样就避免了overtaking现象:可能导致线程未察觉节点被其他线程删除。这种方式减小了锁的粒度,但是由于插入和删除操作在链表的不同位置可能相互阻碍,而限制了并发性.
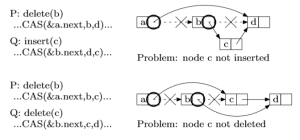
一种解决这个问题的途径就是设计出一个无锁的 linked lists。实现出这样一个无锁的有序linked lists的困难在于要确保在插入或者删除操作期间,相邻的节点仍然是有效的,即他们仍然存在于列表当中并且是相邻的。正如1.4节中图1.6展现的一样,设计出这样一个无锁的链表不是一件轻松的活。
图1.6:基于CAS的链表操作是复杂的。在图中的两个例子(这两个例子都滥用了CAS操作)中,P从链表中将b元素删除。在上面的例子中,Q尝试将c元素插入到链表中,在下面的例子中,Q元素尝试将c元素从链表中删除。圆圈标记的位置代表了CAS操作的目标地址,叉号标记的链接代表在CAS成功之前链接。
第一个基于CAS的无锁链表是Valois 提出来的,他在每个普通节点之前使用了一个特殊的辅助节点来防止在图1.6中发生的非期望现象。Valois的算法在结合了Michael和Scott的内存管理方案之后是正确的,但是这种解决方式并不实用。Harris提出了一种使用了特殊的,带有被原子访问的“删除”标记位的无锁链表,用来标记该节点是否已经被删除,然而此方案只有在垃圾收集环境下才是适用的。Michael 通过修改Harris的算法使其兼容内存回收方法,弥补了这个缺陷。