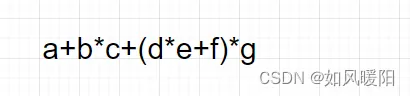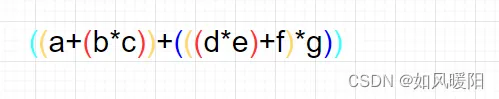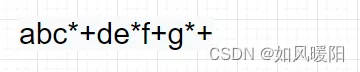1.用栈实现队列
【力扣题目链接】
题意:
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
实现 MyQueue 类:
void push(int x) 将元素 x 推到队列的末尾
int pop() 从队列的开头移除并返回元素
int peek() 返回队列开头的元素
boolean empty() 如果队列为空,返回 true ;否则,返回 false
说明:
你 只能 使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
思路:
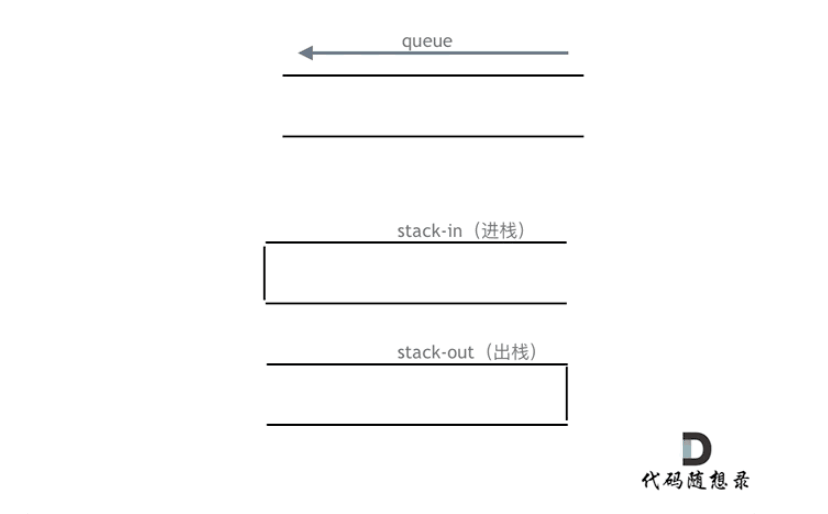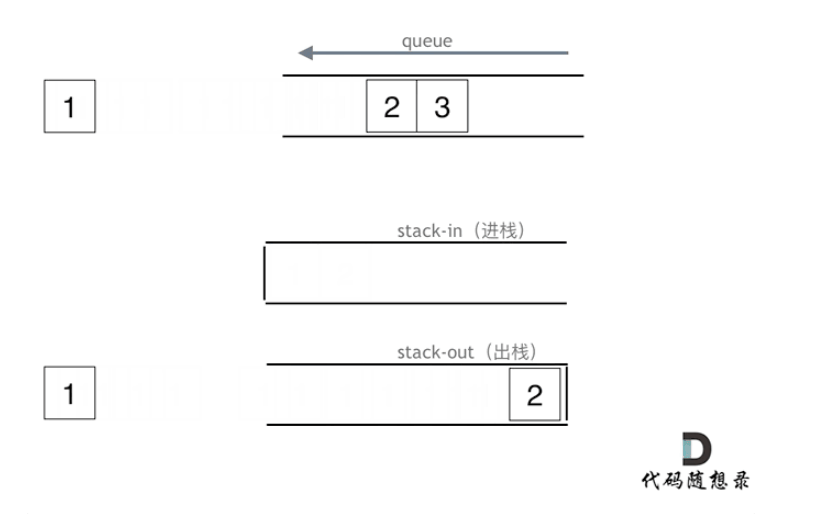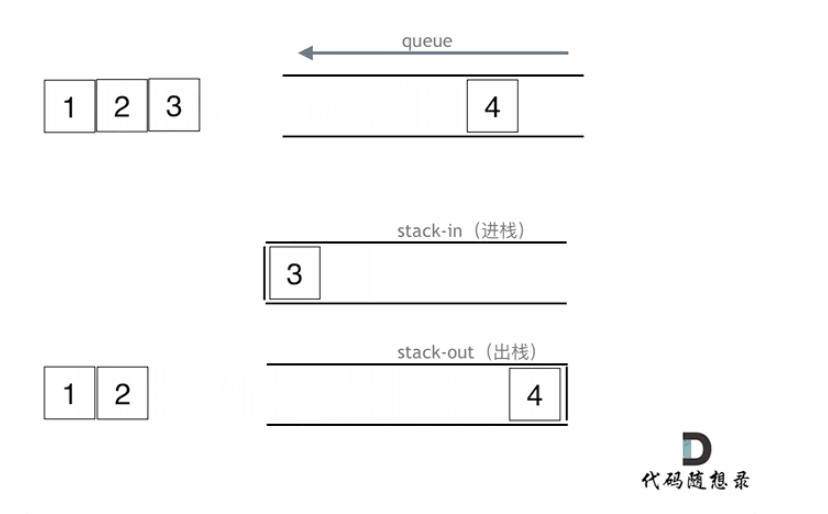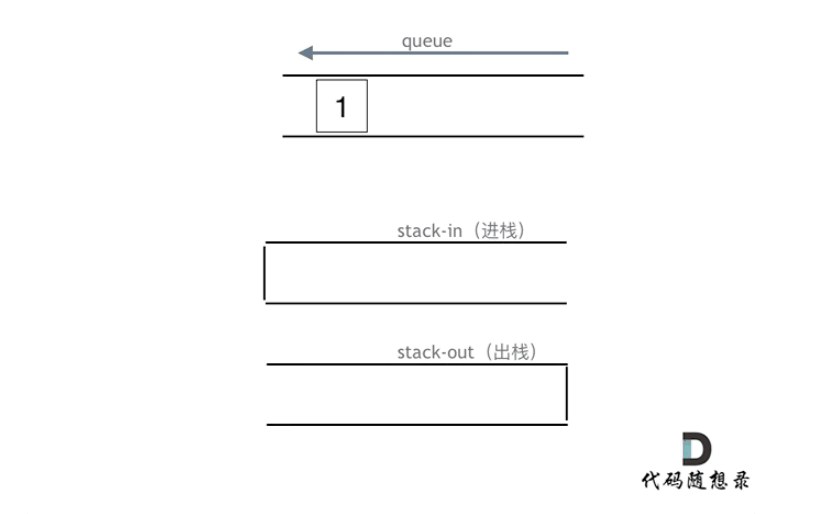
入队列时入进栈,出队列时把数据从入栈出,进出栈内,再从出栈出数据,就是利用两个栈,来调整了数据的顺序,就模拟实现了队列的先进先出。
代码:
class MyQueue { Stack<Integer> stackIn; Stack<Integer> stackOut; public MyQueue() { stackIn=new Stack<>(); stackOut=new Stack<>(); } public void push(int x) { stackIn.push(x); } public int pop() { fun(); return stackOut.pop(); } public int peek() { fun(); return stackOut.peek(); } public boolean empty() { //当两个栈中都没有数据时,模拟队列为空 return stackIn.isEmpty()&&stackOut.isEmpty(); } private void fun() { //当出栈不为空时,直接返回,此时可以直接从出栈出数据 //当出栈为空时,需要把入栈内的数据全部出到出栈中。 if(!stackOut.isEmpty()) return; while (!stackIn.isEmpty()) { stackOut.push(stackIn.pop()); } } } /** * Your MyQueue object will be instantiated and called as such: * MyQueue obj = new MyQueue(); * obj.push(x); * int param_2 = obj.pop(); * int param_3 = obj.peek(); * boolean param_4 = obj.empty(); */
2.用队列实现栈
【力扣题目链接】
题意:
使用队列实现栈的下列操作:
push(x) – 元素 x 入栈
pop() – 移除栈顶元素
top() – 获取栈顶元素
empty() – 返回栈是否为空
注意:
你只能使用队列的基本操作-- 也就是 push to back, peek/pop from front, size, 和 is empty 这些操作是合法的。
你所使用的语言也许不支持队列。 你可以使用 list 或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
你可以假设所有操作都是有效的(例如, 对一个空的栈不会调用 pop 或者 top 操作)。
思路:
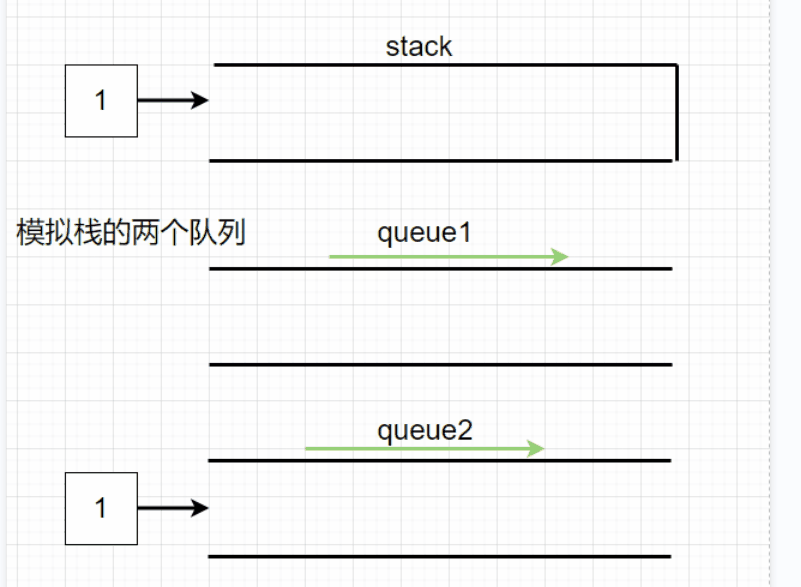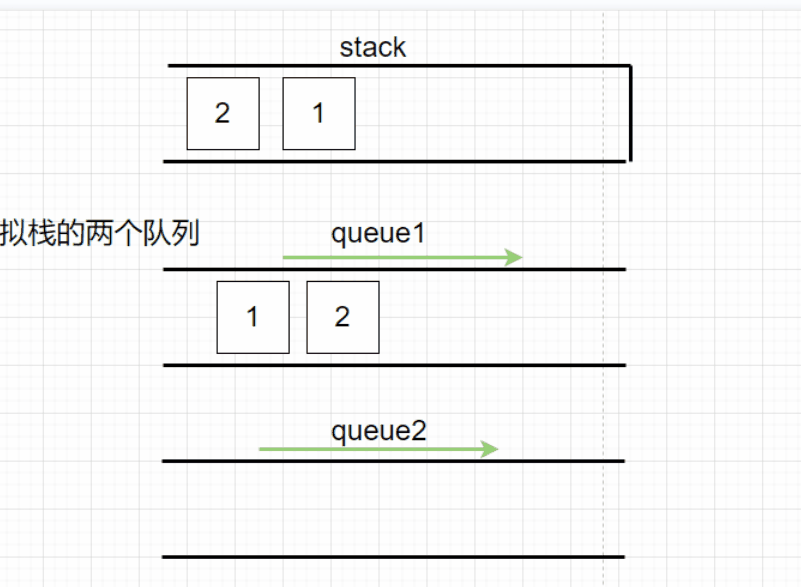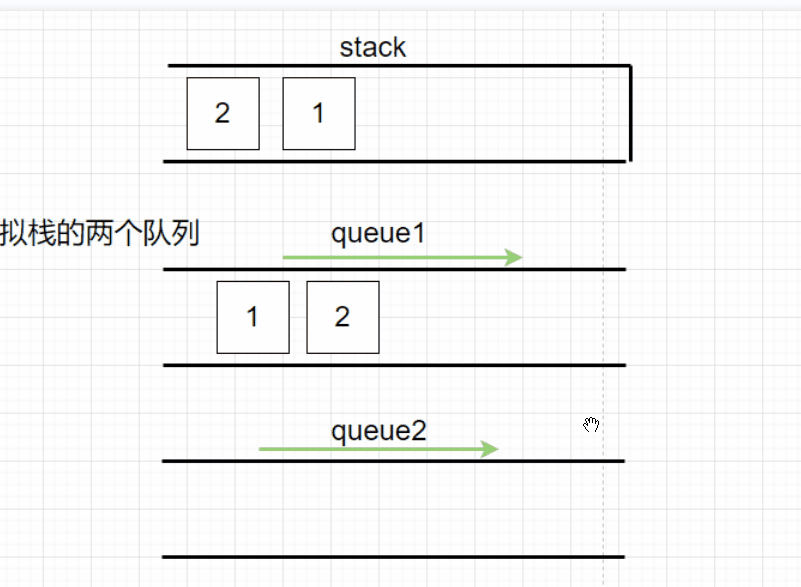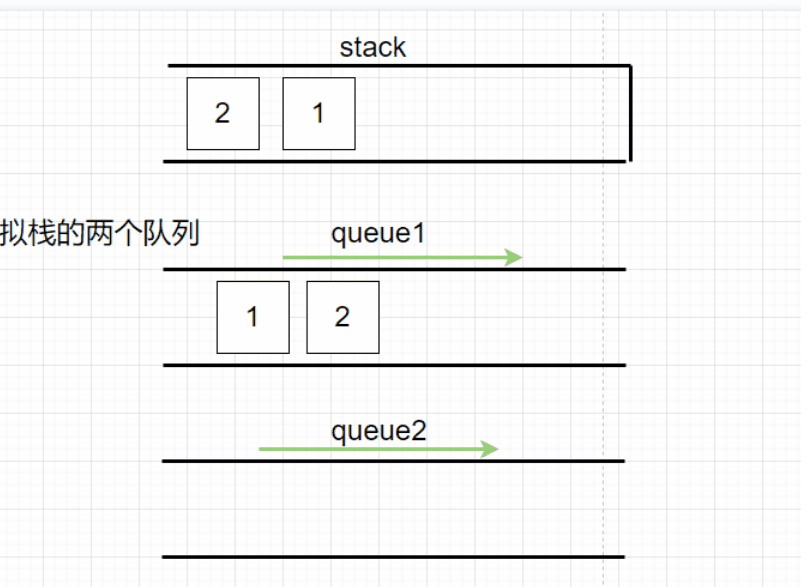
用队列来模拟栈的先进后出,此时就需要通过两个栈来更改数据的顺序,来模拟实现先进后出。
在每次新入元素时,让该元素先进入queue2中,如果queue1中元素不为空,就让queue1中元素依次出队列进入queue2中,再交换queue1和queue2,这样就可以通过queue2调整元素的顺序,使得每次放入新数据时模拟是放进了栈顶,使得queue1中的元素顺序模拟了栈的先入后出。
代码:
class MyStack { Queue<Integer> queue1; Queue<Integer> queue2; public MyStack() { queue1=new LinkedList<>(); queue2=new LinkedList<>(); } public void push(int x) { queue2.offer(x); while (!queue1.isEmpty()) { queue2.offer(queue1.poll()); } //交换queue1和queue2,交换完成后queue1成为模拟栈,queue2又变为空 Queue<Integer> temp=queue1; queue1=queue2; queue2=temp; } public int pop() { return queue1.poll(); } public int top() { return queue1.peek(); } public boolean empty() { return queue1.isEmpty(); } } /** * Your MyStack object will be instantiated and called as such: * MyStack obj = new MyStack(); * obj.push(x); * int param_2 = obj.pop(); * int param_3 = obj.top(); * boolean param_4 = obj.empty(); */
3.有效的括号
【力扣题目链接】
题意:
给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。
示例 1:
输入: “()”
输出: true
示例 2:
输入: “()[]{}”
输出: true
示例 3:
输入: “(]”
输出: false
示例 4:
输入: “([)]”
输出: false
示例 5:
输入: “{[]}”
输出: true
思路:
共有三种无效方式:
- 1.左右括号不匹配 "{(}}"
- 2.左括号多"(()"
- 3.右括号多"())"
将给定的字符串从头开始遍历,遇见左括号就对应入栈右括号(比如:遇见"{",就对应入栈"}"),在遇到不是左括号的情况下去出栈并比对括号是否一致,如果刚好遍历完字符串栈也为空,则说明为有效括号。
代码:
class Solution { public boolean isValid(String s) { Stack<Character> stack=new Stack<>(); char ch; for(int i=0;i<s.length();i++) { ch=s.charAt(i); if(ch=='(') stack.push(')'); else if(ch=='{') stack.push('}'); else if(ch=='[') stack.push(']'); //如果再遍历完之前栈为空,说明右括号多;如果不匹配也直接返回false else if(stack.isEmpty()||ch!=stack.pop()) return false; } //如果遍历完后栈不为空,说明左括号多;遍历完后栈刚好为空则为有效括号 return stack.isEmpty(); } }
4.删除字符串中的所有相邻重复项
【力扣题目链接】
题意:
给出由小写字母组成的字符串 S,重复项删除操作会选择两个相邻且相同的字母,并删除它们。
在 S 上反复执行重复项删除操作,直到无法继续删除。
在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。
示例:
输入:“abbaca”
输出:“ca”
解释:例如,在 “abbaca” 中,我们可以删除 “bb” 由于两字母相邻且相同,这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 “aaca”,其中又只有 “aa” 可以执行重复项删除操作,所以最后的字符串为 “ca”。
提示:
1 <= S.length <= 20000
S 仅由小写英文字母组成。
思路:
我们在放入新字符时,需要判断前一个字符是否与之相等,所以需要利用栈来实现。当栈为空时,直接放入字符,其后每次放入时都需要和栈顶元素判断是否相同,相同的情况下栈顶元素弹出。
代码:
法一:
双端队列实现栈(与栈的用法相同,但用双端队列实现栈效率更高)
class Solution { public String removeDuplicates(String s) { Deque<Character> stack=new LinkedList<>(); for(int i=0;i<s.length();i++) { char ch=s.charAt(i); //如果栈为空或者栈顶字符与要放入的字符不相同,则入栈新字符 if(stack.isEmpty()||stack.peek()!=ch) stack.push(ch); //否则就是字符相同,弹出栈顶元素 else stack.pop(); } //利用StringBuffer拼接字符串 StringBuffer sb=new StringBuffer(); while(!stack.isEmpty()) { sb.append(stack.pop()); } //倒置后返回 return sb.reverse().toString(); } }
法二:
直接利用StringBuffer模拟实现栈
class Solution { public String removeDuplicates(String s) { StringBuilder sb=new StringBuilder(); //前一个字符的角标 int index=-1; for(int i=0;i<s.length();i++) { char ch=s.charAt(i); if(index>=0&&ch==sb.charAt(index)) { sb.deleteCharAt(index--); }else { sb.append(ch); index++; } } return sb.toString(); } }
5.逆波兰表达式求值
【力扣题目链接】
题意:
根据 逆波兰表示法,求表达式的值。
有效的算符包括 +、-、*、/ 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
注意 两个整数之间的除法只保留整数部分。
可以保证给定的逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
示例 1:
输入:tokens = [“2”,“1”,“+”,“3”,“*”]
输出:9
解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
示例 2:
输入:tokens = [“4”,“13”,“5”,“/”,“+”]
输出:6
解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
思路:
拓展:
给定中缀表达式转前缀后缀表达式的方法:
1.给每一步运算都加上括号
2.把符号都移到对应括号的外边(移到对应括号后边就是后缀表达式,移到对应括号前边就是前缀表达式)
3.去掉所有括号,得到前缀或者后缀表达式
上边扩充的是一些题外知识,该题的思路就是利用栈来完成运算,运算规则是:
如果是数字就入栈,如果是符号则不入栈,弹出栈顶两个元素,先弹出的为右操作数,后弹出的为左操作数,完成运算后入栈运算结果,最后返回最后的运算结果(栈中也就只有一个元素了)。
代码:
class Solution { public int evalRPN(String[] tokens) { Stack<Integer> stack=new Stack<>(); for(String s:tokens) { if(!isOperation(s)) { //不是操作符就进行入栈 stack.push(Integer.parseInt(s)); }else { int num2=stack.pop(); int num1=stack.pop(); switch (s) { case "+": stack.push(num1+num2); break; case "-": stack.push(num1-num2); break; case "*": stack.push(num1*num2); break; case "/": stack.push(num1/num2); break; } } } return stack.peek(); } //判断是否为操作符 private boolean isOperation(String s) { if(s.equals("+")||s.equals("-")||s.equals("*")||s.equals("/")) return true; return false; } }
6.滑动窗口最大值
【力扣题目链接】
题意:
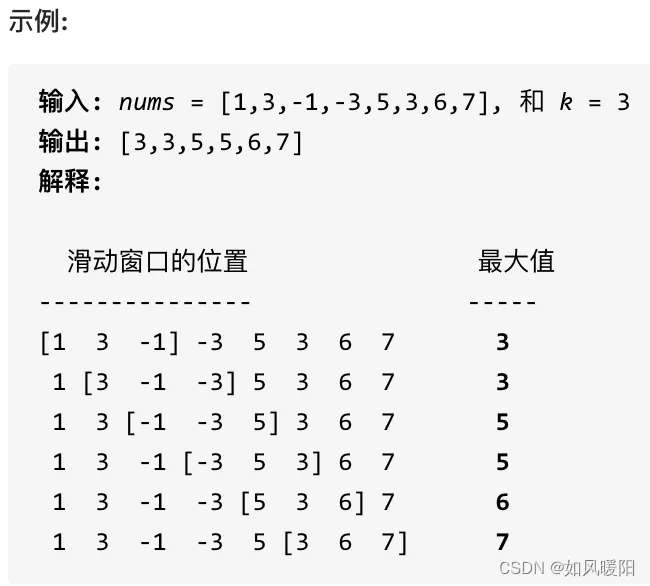
给定一个数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
思路:
该题利用双端队列来维系一个单调队列,在该单调队列中,队首元素就对应窗口的最大值(在该队列中存储数组的下标),窗口右移便意味着需要左边删除一个元素,右边新添加一个元素,如果右移以后单调队列中的队首元素对应的角标不在窗口内,则需要删除队首元素。右移添加的元素如果小于或等于队尾元素,也需要入队列,但如果大于队尾元素,为了维系单调队列,则需要删除队尾元素再次进行比较,直至再次变为单调队列。通过这样操作,单调队列的队首便对应每个窗口的最大元素,将其存储在数组中返回即可。
代码:
class Solution { public int[] maxSlidingWindow(int[] nums, int k) { Deque<Integer> deque = new LinkedList<>(); int n = nums.length; //新建返回数组,长度为n-k+1(移动的次数,每次移动对应一个窗口,每个窗口对应一个最大值) int[] res = new int[n - k + 1]; //返回数组的下标 int idx = 0; for(int i = 0; i < n; i++) { // 根据题意,i为nums下标,是要在[i - k + 1, i] 中选到最大值,只需要保证两点 // 1.队列头结点需要在[i - k + 1, i]范围内,不符合则要弹出 while(!deque.isEmpty() && deque.peek() < i - k + 1){ deque.poll(); } // 2.既然是单调,就要保证每次放进去的数字要比末尾的都大,否则也弹出 while(!deque.isEmpty() && nums[deque.peekLast()] < nums[i]) { deque.pollLast(); } deque.offer(i); // 因为单调,当i增长到符合第一个k范围的时候,每滑动一步都将队列头节点放入结果就行了 if(i >= k - 1){ res[idx++] = nums[deque.peek()]; } } return res; } }
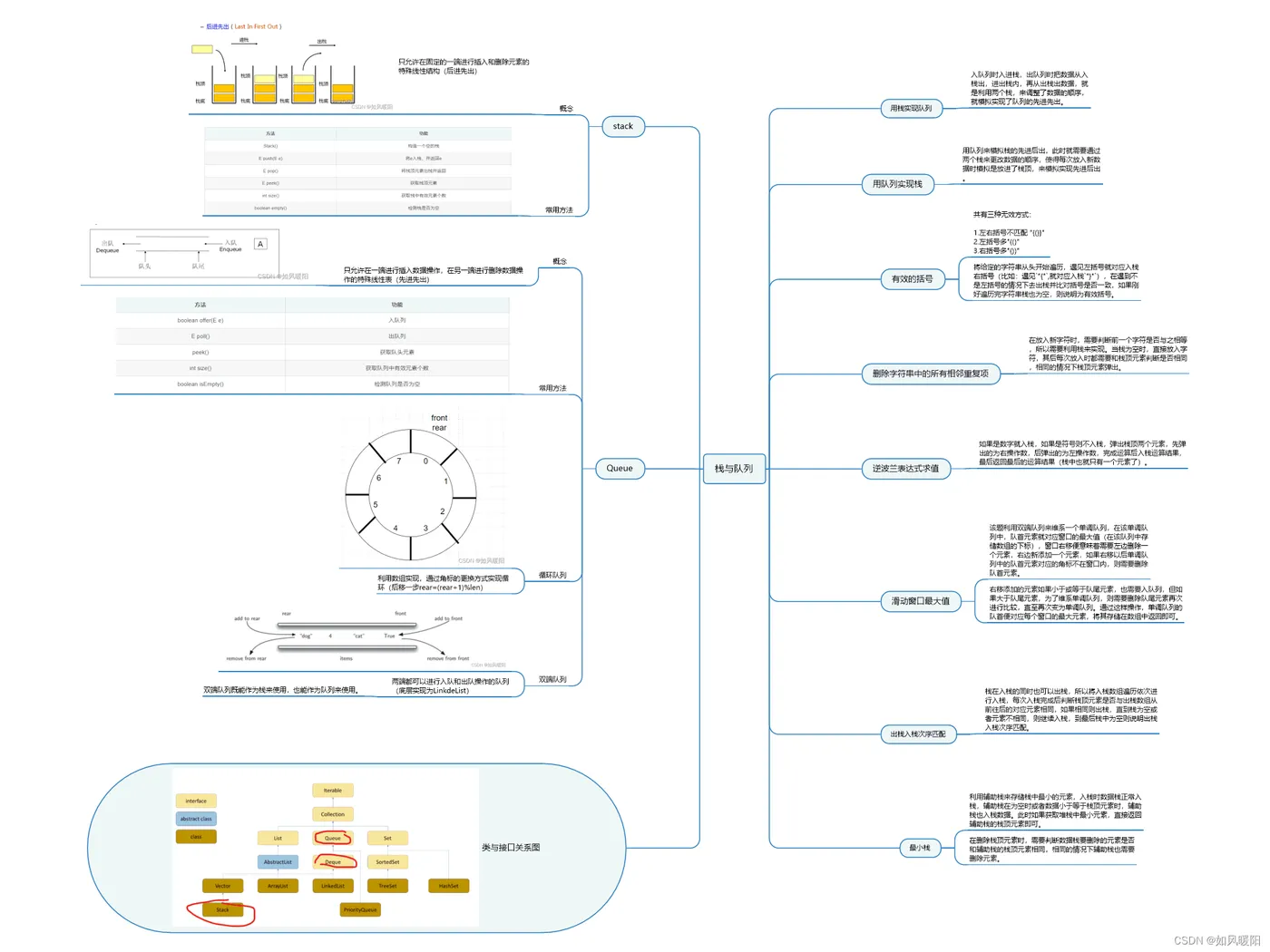
导图总结