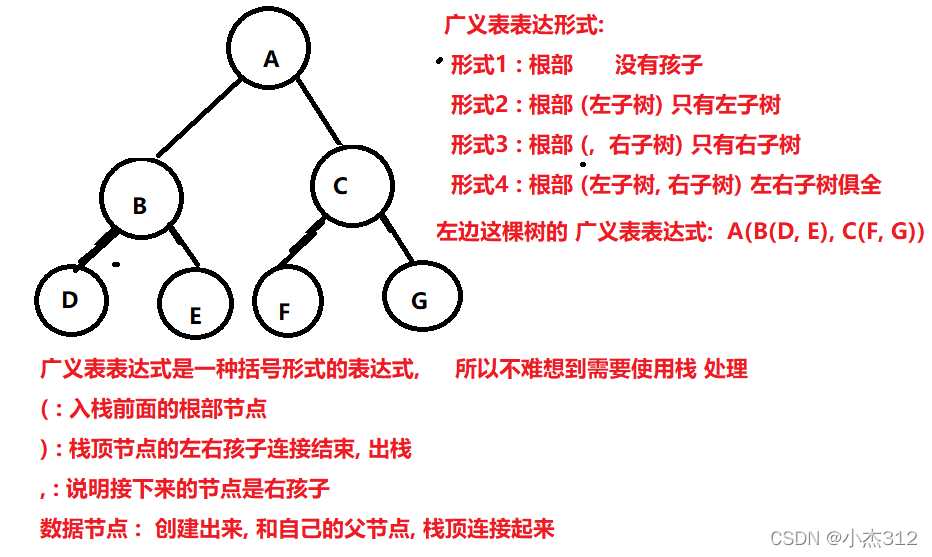
一, 理论支撑图解
二. 动态图解实例刨析过程, 使用栈模拟
仅仅上述图解, 可以大致理解这个广义表表达形式, 但是还是奈何这个过程是抽象的, 难以通过几句话完全理解整个过程, 如下就是使用栈来一步一步的模拟整个过程
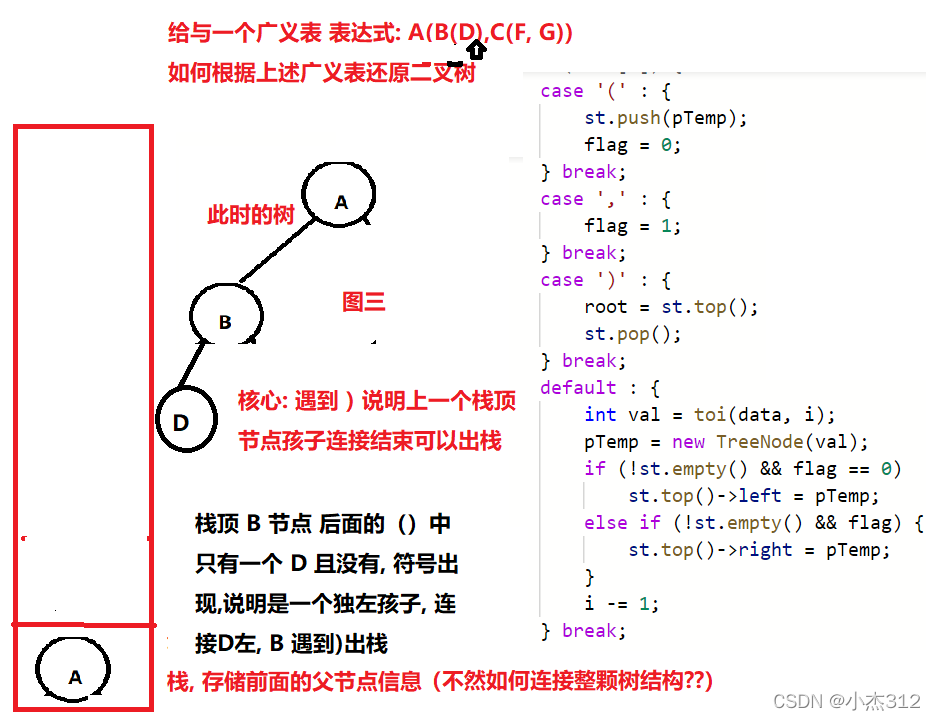
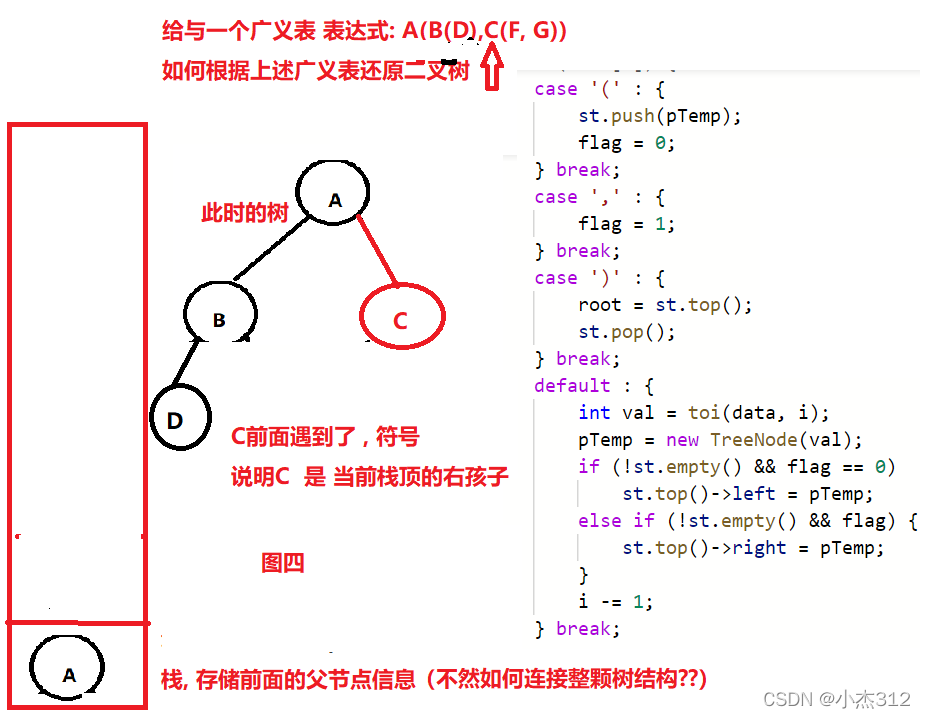
遇到左括号, 说明前面一定存在一个创建好的当前父亲节点, 我们将其入栈, 因为在他对应的右括号到来之前需要连接自己的孩子节点, 自己需要存储在栈中, 以便连接自己的孩子节点
- 遇到右括号, 说明当前栈顶元素, 所有孩子节点连接结束, 出栈顶
遇到逗号标记右孩子, 改变标记. 左括号重置标记为1, 不然上一轮 标记的右会影响后面
继续 遇到 左括号 入栈 前面的 父亲节点, 为何入栈, 后面的孩子节点需要连接父亲节点, 故而需要入栈,连接的时候如何判断是左右孩子, 利用flag做标记
然后继续重复上述 最终建成此树:
核心关键 : 为何 需要栈结构, 后进的 需要先出, 又特别是二叉树, 一棵树:
根部 左子树 右子树:
根部节点 肯定是先等待自己的左子树 根部先当栈顶连接完全左子树的孩子之后, 根部 才能连接自己的右子树, 所以 前面父亲节点就需要压在下面等待上面的 节点连接完成之后 自己才能连接, 这个过程 有点像 后序遍历的意思了, 先处理完自己的 左右子树, 最后处理自己, 所以虽然自己在前面但是需要压在栈下面
最后出的一个节点是根部节点 : 整棵树的根部节点
最后 广义表建树 代码 如题目 :
class Codec { public: // Encodes a tree to a single string. string serialize(TreeNode* root) { string ans = ""; if (root == NULL) return ans; stringstream in_out; in_out << root->val; in_out >> ans; //整形转换为string if (root->left || root->right) ans += "("; ans += serialize(root->left); if (root->right) ans += ","; ans += serialize(root->right); if (root->left || root->right) ans += ")"; return ans; } int toi(string& s, int& i) { int val = 0; bool flag = 0; if (s[i] == '-') { flag = 1; i += 1; } for (; s[i] >= '0' && s[i] <= '9'; ++i) { val = val * 10 + (s[i] - '0'); } if(flag) val *= -1; return val; } // Decodes your encoded data to tree. TreeNode* deserialize(string data) { TreeNode* root = NULL, *pTemp = NULL; stack<TreeNode* > st; bool flag = 0; for (int i = 0; i < data.size(); ++i) { switch(data[i]) { case '(' : { st.push(pTemp); flag = 0; } break; case ',' : { flag = 1; } break; case ')' : { root = st.top(); st.pop(); } break; default : { int val = toi(data, i); pTemp = new TreeNode(val); if (!st.empty() && flag == 0) st.top()->left = pTemp; else if (!st.empty() && flag) { st.top()->right = pTemp; } i -= 1; } break; } } if (root == NULL && pTemp) root = pTemp; return root; } };
三. 总结
针对栈结构, 很多时候栈模拟过程 是一个非常好的理解栈结构类题目的方式,,, 我们手绘一个栈, 将代码逻辑带入到栈中去走, 这种方式很多时候 对于栈的理解 和 代码理解会变得容易很多
二叉树, 做二叉树的题目: 二叉树的 后序遍历 很多时候起着至关重要的角色, 很多题目有形无形, 都体现了 需要先处理 左右子树 然后处理根部的 这样一种思路,.......
最后再回顾一下广义表转二叉树核心几点:
栈保存前面的 父亲节点 方便后序树结构的连接
遇到 ( 说明前面的节点存在孩子, 也说明前面是一个父节点(存在孩子), 所以需要入栈
遇到逗号说明接下来是一个右孩子, 所以需要改标记
遇到 右括号说明当前栈顶,已完成所有孩子连接工作, 出栈