31题解–整数中1出现的次数

题目描述

求出1到13的整数中1出现的次数,并算出100~1300的整数中1出现的次数？为此他特别数了一下1到13中包含1的数字有1、10、11、12、13因此共出现6次,但是对于后面问题他就没辙了。ACMer希望你们帮帮他,并把问题更加普遍化,可以很快的求出任意非负整数区间中1出现的次数（从1 到 n 中1出现的次数）。

思路解析

这里我是暴力的，主要注意一下int，string，char之间的转换即可。

源代码

public class Solution {
    public int NumberOf1Between1AndN_Solution(int n)
   {
     int count=0;
     for(int i=1;i<n+1;i++)
     {
       String str=String.valueOf(i);
       char[]ch=str.toCharArray();
       for(int j=0;j<ch.length;j++)
       {
         if(ch[j]=='1')
           count++;
       }
     }
     return count;
   }
}

32题解–把数组排成最小的数

题目描述

输入一个正整数数组，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。例如输入数组{3，32，321}，则打印出这三个数字能排成的最小数字为321323。

思路解析

这里最简单的办法就是全排列输出所有的数字排列然后进行比较但是这样会出现很多重复的情况，比如说出现{321,321}时，他就会出现两种情况。这里是采用给数组排序定义一个排序规则即可，具体代码中有。

源代码

import java.util.Arrays;
import java.util.Comparator;
public class Solution {
   public String PrintMinNumber(int [] numbers) {
     String str="";
     Integer[]num=new Integer[numbers.length];
     for(int i=0;i<num.length;i++)
       num[i]=numbers[i];
     Arrays.sort(num,comparator);
     for(int i=0;i<num.length;i++)
       str+=String.valueOf(num[i]);
     return str;
      }
  //定义数组的排序规则，同样也适用于对象列表，队列等数据结构
  Comparator<Integer>comparator=new Comparator<Integer>() {
    @Override
    public int compare(Integer o1, Integer o2) {
      int sum1=Integer.parseInt(String.valueOf(o1)+String.valueOf(o2));
            int sum2=Integer.parseInt(String.valueOf(o2)+String.valueOf(o1));
      return sum1-sum2;
    }
  };
}

33题解–丑数（太特么重要了）*******

题目描述

把只包含质因子2、3和5的数称作丑数（Ugly Number）。例如6、8都是丑数，但14不是，因为它包含质因子7。习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数。

思路解析

这里博主用自己的方法跑了80%的样例，一开始就是十几这种小玩意儿，但是后来就突然跑到1500位，算法的复杂度太高了没能跑出来，在这里借鉴了一下别人的思路，是真的给力。

因为丑数是只包含2,3,5这三个质因子的数，所以可以得出丑数的通用公式如下：

又因为他要求我们是从小到大排序然后输出，所以我们就需要对满足这种格式的数据进行排序，但是这里的难点就是我们如何才能实现排序的

思路是既然通用公式已经确定，我们也不能看出其实数据从后部分开始一定都是前某一项的倍数，而且这个倍数一定是由2,3,5交叉组合而成，所以我们只需要通过判断，将次结算之后最小的那个数添加到我们的数组中即可，但是也不要顽疾通过光标来计数，2,3,5这三个质因子的位置。

源代码

public class Solution {
  public int GetUglyNumber_Solution(int index) {
        if(index <= 0)return 0;
        int p2=0,p3=0,p5=0;//初始化三个指向三个潜在成为最小丑数的位置
        int[] result = new int[index];
        result[0] = 1;//
        for(int i=1; i < index; i++){
            result[i] = Math.min(result[p2]*2, Math.min(result[p3]*3, result[p5]*5));
            if(result[i] == result[p2]*2)p2++;//为了防止重复需要三个if都能够走到
            if(result[i] == result[p3]*3)p3++;//为了防止重复需要三个if都能够走到
            if(result[i] == result[p5]*5)p5++;//为了防止重复需要三个if都能够走到
        }
        return result[index-1];
    }
}

34题解–第一次只出现一次的字符

题目描述

在一个字符串(0<=字符串长度<=10000，全部由字母组成)中找到第一个只出现一次的字符,并返回它的位置, 如果没有则返回 -1（需要区分大小写）.（从0开始计数）

思路解析

这里我选择的是重新定义一个对象用来存储我们需要的信息，包括字符出现的次数以及该字符以及首次出现时的下标，之后我们只需要将字符一次存入set之后同时进行判断，如果是第一进入就不仅存入set同时存进list之中，否则就说明list中已经有该对象字符了，我们只需要将该对象的val+1即可。最后检测有误只出现一次的字符即可，并且返回相应的数值。

源代码

import java.util.ArrayList;
import java.util.HashSet;
import java.util.List;
import java.util.Set;
public class Solution {
   public  class Node {
        //存储出现的次数
      int val;
      //存储该字符
      char ch;
      //存储字符下标
      int address;
      Node(char ch,int address) {
          this.ch =ch;
          this.address=address;
          this.val=1;
      }
  }
   public int FirstNotRepeatingChar(String str) {
     int flag=-1;
     char[]ch=str.toCharArray();
     //去重后的字符
     Set<Character>set=new HashSet<Character>();
     List<Node>list=new ArrayList<Node>();
     for(int i=0;i<ch.length;i++)
     {
         //字符首次出现添加到set与list中
       if(!set.contains(ch[i]))
       {
         set.add(ch[i]);
         Node node=new Node(ch[i], i);
         list.add(node);
       }
       //多次出现就开始改变node对象的val
       else
       {
         for(int j=0;j<list.size();j++)
         {
           if(list.get(j).ch==ch[i])
             list.get(j).val++;
         }
       }
     }
     //检查是否有只出现过一次的字符，有则直接输出相应的下标
     for(int i=0;i<list.size();i++)
     {
       if(list.get(i).val==1)
       {
         flag=list.get(i).address;
         break;
       }
     } 
     return flag;
   }
}

35题解–数组中的逆序对

题目描述

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。即输出P%1000000007

题目保证输入的数组中没有的相同的数字

数据范围：

对于%50的数据,size<=10^4
对于%75的数据,size<=10^5
对于%100的数据,size<=2*10^5
示例1
输入
1,2,3,4,5,6,7,0
输出
7

思路解析

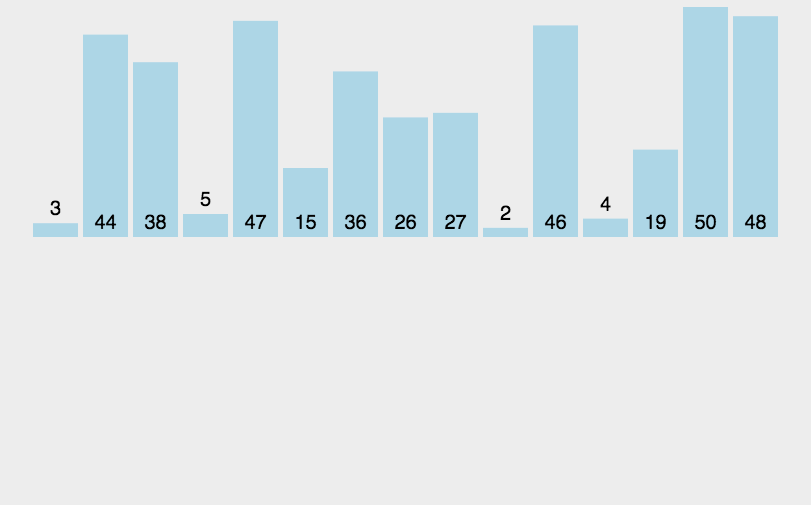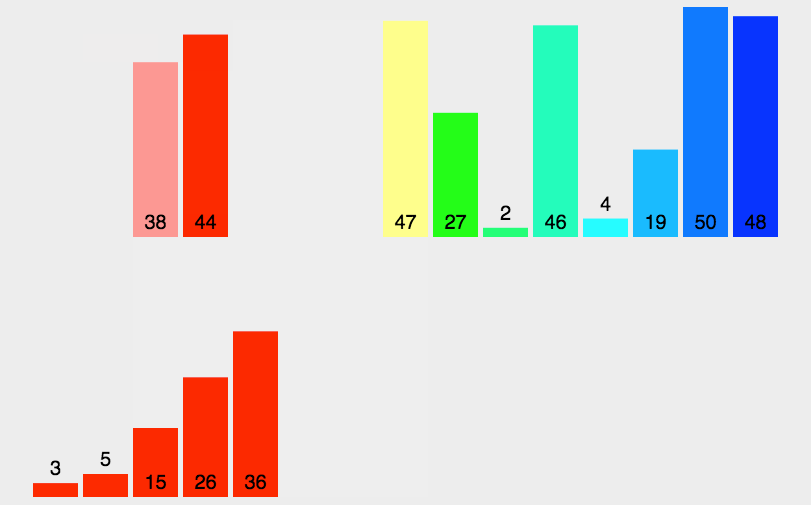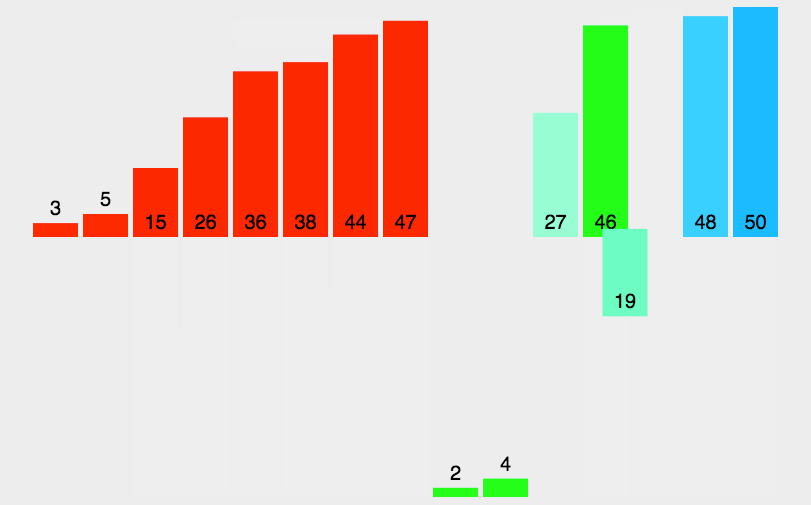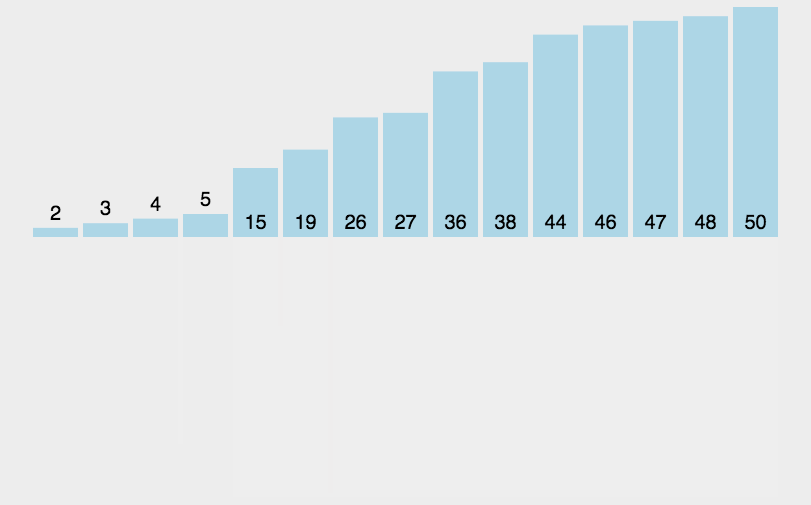
其实求逆序数的本质就是冒泡排序过程中的元素交换次数，但是后来的数据量如果还是通过冒泡排序进行测量交换次数的话，显然时间一定是会超的，所以这里我们选择通过归并排序来实现。

还是放上之前的一张模拟图帮助大家理解。

public class Solution {
    static int value=0;
    public  int InversePairs(int [] array) {    
      mergesort(array,0,array.length-1);
      return value;
    } 
    private  void mergesort(int[] array, int l, int r) {
      int mid=(l+r)/2;
      if(l<r)
      {
        mergesort(array, l, mid);
        mergesort(array, mid+1, r);
        merge(array, l,mid, r);
      }
    }
    //合并两个区间
    private  void merge(int[] array, int l, int mid, int r) {
      int left=l;int right=mid+1;
      int num[]=new int[r-l+1];
      int index=0;
      //两个区间都未超过边界
      while (left<=mid&&right<=r) {
            //左区间目前是较小的值，所以直接赋值即可
        if(array[left]<=array[right])
        {
          num[index++]=array[left++];
        }
        else {  
        //区间目前是较大的值。所以很明显left-mid区间的值都是小于left位置上的值，所以符合逆序数的规则，开始计数      
          num[index++]=array[right++];
          value+=mid-left+1;
                  value%=1000000007;
        }
      }
      //已经有一个区间已经匹配结束了
      //这里是右区间匹配结束，只需要依次将左区间的值赋值即可
      while(left<=mid)
          {
        num[index++]=array[left++];
          }
        //这里是左区间匹配结束，只需要依次将右区间的值赋值即可
      while(right<=r)
          {
        num[index++]=array[right++];
          } 
      for(int i=0;i<index;i++)
      {
        array[l+i]=num[i];
      } 
    }
}