目录
基于datasets糖尿病数据集利用LassoR和RidgeR算法(alpha调参)进行(9→1)回归预测
相关文章
ML之LassoR&RidgeR:基于datasets糖尿病数据集利用LassoR和RidgeR算法(alpha调参)进行(9→1)回归预测
ML之LassoR&RidgeR:基于datasets糖尿病数据集利用LassoR和RidgeR算法(alpha调参)进行(9→1)回归预测实现
基于datasets糖尿病数据集利用LassoR和RidgeR算法(alpha调参)进行(9→1)回归预测
设计思路
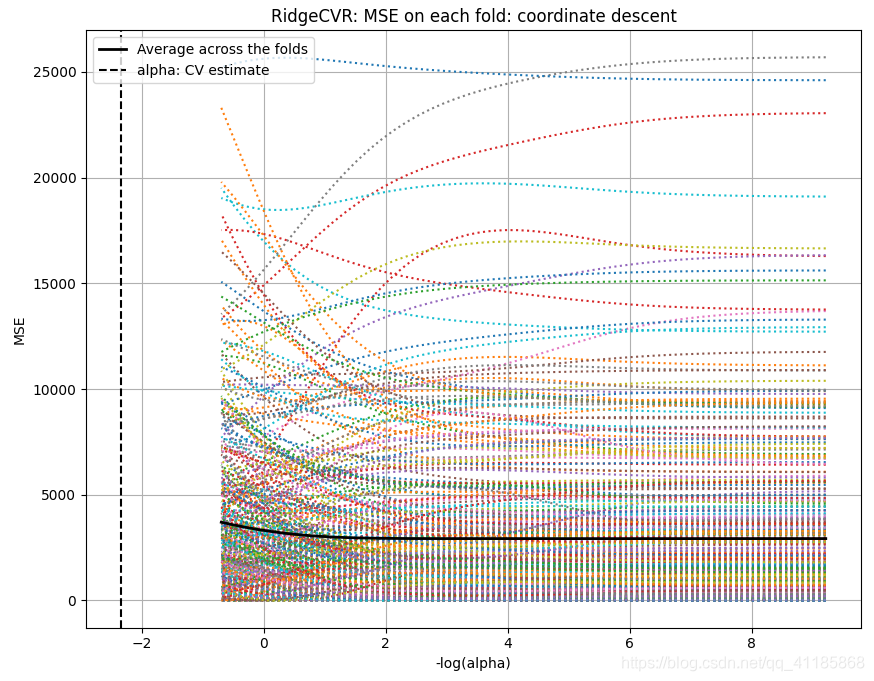
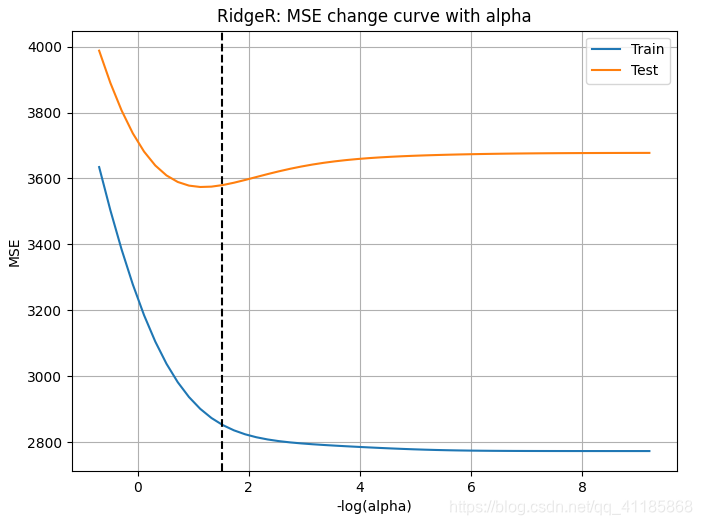
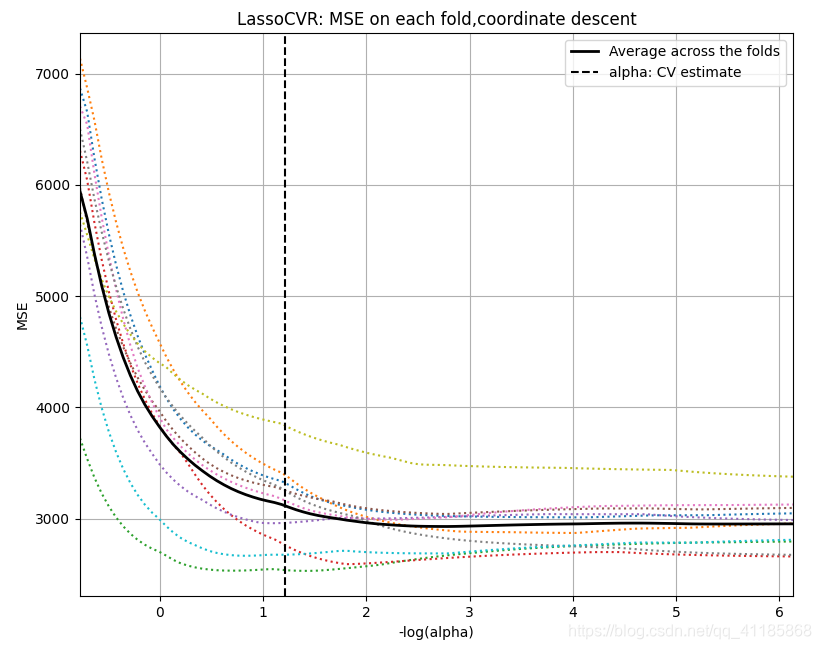
输出结果
1. .. _diabetes_dataset: 2. 3. Diabetes dataset 4. ---------------- 5. 6. Ten baseline variables, age, sex, body mass index, average blood 7. pressure, and six blood serum measurements were obtained for each of n = 8. 442 diabetes patients, as well as the response of interest, a 9. quantitative measure of disease progression one year after baseline. 10. 11. **Data Set Characteristics:** 12. 13. :Number of Instances: 442 14. 15. :Number of Attributes: First 10 columns are numeric predictive values 16. 17. :Target: Column 11 is a quantitative measure of disease progression one year after baseline 18. 19. :Attribute Information: 20. - age age in years 21. - sex 22. - bmi body mass index 23. - bp average blood pressure 24. - s1 tc, T-Cells (a type of white blood cells) 25. - s2 ldl, low-density lipoproteins 26. - s3 hdl, high-density lipoproteins 27. - s4 tch, thyroid stimulating hormone 28. - s5 ltg, lamotrigine 29. - s6 glu, blood sugar level 30. 31. Note: Each of these 10 feature variables have been mean centered and scaled by the standard deviation times `n_samples` (i.e. the sum of squares of each column totals 1). 32. 33. Source URL: 34. https://www4.stat.ncsu.edu/~boos/var.select/diabetes.html 35. 36. For more information see: 37. Bradley Efron, Trevor Hastie, Iain Johnstone and Robert Tibshirani (2004) "Least Angle Regression," Annals of Statistics (with discussion), 407-499. 38. (https://web.stanford.edu/~hastie/Papers/LARS/LeastAngle_2002.pdf) 39. age sex bmi bp ... s4 s5 s6 target 40. 0 0.038076 0.050680 0.061696 0.021872 ... -0.002592 0.019908 -0.017646 151.0 41. 1 -0.001882 -0.044642 -0.051474 -0.026328 ... -0.039493 -0.068330 -0.092204 75.0 42. 2 0.085299 0.050680 0.044451 -0.005671 ... -0.002592 0.002864 -0.025930 141.0 43. 3 -0.089063 -0.044642 -0.011595 -0.036656 ... 0.034309 0.022692 -0.009362 206.0 44. 4 0.005383 -0.044642 -0.036385 0.021872 ... -0.002592 -0.031991 -0.046641 135.0 45. 46. [5 rows x 11 columns] 47. alphas: 50 [1.00000000e-03 1.16779862e-03 1.36375363e-03 1.59258961e-03 48. 1.85982395e-03 2.17189985e-03 2.53634166e-03 2.96193630e-03 49. 3.45894513e-03 4.03935136e-03 4.71714896e-03 5.50868007e-03 50. 6.43302900e-03 7.51248241e-03 8.77306662e-03 1.02451751e-02 51. 1.19643014e-02 1.39718947e-02 1.63163594e-02 1.90542221e-02 52. 2.22514943e-02 2.59852645e-02 3.03455561e-02 3.54374986e-02 53. 4.13838621e-02 4.83280172e-02 5.64373920e-02 6.59075087e-02 54. 7.69666979e-02 8.98816039e-02 1.04963613e-01 1.22576363e-01 55. 1.43144508e-01 1.67163960e-01 1.95213842e-01 2.27970456e-01 56. 2.66223585e-01 3.10895536e-01 3.63063379e-01 4.23984915e-01 57. 4.95129000e-01 5.78210965e-01 6.75233969e-01 7.88537299e-01 58. 9.20852773e-01 1.07537060e+00 1.25581631e+00 1.46654056e+00 59. 1.71262404e+00 2.00000000e+00] 60. {'alpha': 0.07696669794067007} 61. 0.472 (+/-0.177) for {'alpha': 0.0010000000000000002} 62. 0.472 (+/-0.177) for {'alpha': 0.0011677986237376523} 63. 0.472 (+/-0.177) for {'alpha': 0.0013637536256035543} 64. 0.472 (+/-0.177) for {'alpha': 0.0015925896070970653} 65. 0.472 (+/-0.177) for {'alpha': 0.0018598239513468405} 66. 0.472 (+/-0.176) for {'alpha': 0.002171899850777162} 67. 0.472 (+/-0.176) for {'alpha': 0.0025363416566335814} 68. 0.472 (+/-0.176) for {'alpha': 0.002961936295945173} 69. 0.472 (+/-0.176) for {'alpha': 0.0034589451300033745} 70. 0.472 (+/-0.176) for {'alpha': 0.004039351362401994} 71. 0.472 (+/-0.176) for {'alpha': 0.004717148961805858} 72. 0.472 (+/-0.176) for {'alpha': 0.0055086800655623795} 73. 0.472 (+/-0.176) for {'alpha': 0.00643302899917478} 74. 0.472 (+/-0.176) for {'alpha': 0.007512482411700719} 75. 0.471 (+/-0.175) for {'alpha': 0.008773066621237415} 76. 0.471 (+/-0.174) for {'alpha': 0.010245175126239786} 77. 0.471 (+/-0.174) for {'alpha': 0.011964301412374057} 78. 0.472 (+/-0.173) for {'alpha': 0.013971894723352857} 79. 0.472 (+/-0.173) for {'alpha': 0.016316359428938842} 80. 0.473 (+/-0.172) for {'alpha': 0.01905422208552364} 81. 0.473 (+/-0.171) for {'alpha': 0.02225149432786609} 82. 0.474 (+/-0.170) for {'alpha': 0.025985264452188187} 83. 0.474 (+/-0.169) for {'alpha': 0.03034555606472431} 84. 0.475 (+/-0.167) for {'alpha': 0.03543749860893881} 85. 0.476 (+/-0.166) for {'alpha': 0.04138386210422369} 86. 0.477 (+/-0.164) for {'alpha': 0.04832801721026122} 87. 0.477 (+/-0.162) for {'alpha': 0.05643739198611263} 88. 0.478 (+/-0.160) for {'alpha': 0.06590750868872472} 89. 0.478 (+/-0.157) for {'alpha': 0.07696669794067007} 90. 0.477 (+/-0.154) for {'alpha': 0.08988160392874607} 91. 0.476 (+/-0.151) for {'alpha': 0.10496361336732249} 92. 0.475 (+/-0.148) for {'alpha': 0.12257636323289021} 93. 0.472 (+/-0.145) for {'alpha': 0.1431445082861357} 94. 0.469 (+/-0.143) for {'alpha': 0.1671639597721522} 95. 0.466 (+/-0.139) for {'alpha': 0.19521384216045554} 96. 0.462 (+/-0.134) for {'alpha': 0.22797045620951942} 97. 0.455 (+/-0.129) for {'alpha': 0.2662235850143214} 98. 0.447 (+/-0.126) for {'alpha': 0.31089553618622834} 99. 0.441 (+/-0.122) for {'alpha': 0.3630633792844568} 100. 0.434 (+/-0.117) for {'alpha': 0.42398491465793015} 101. 0.425 (+/-0.112) for {'alpha': 0.49512899982305664} 102. 0.412 (+/-0.107) for {'alpha': 0.5782109645659657} 103. 0.395 (+/-0.105) for {'alpha': 0.675233968650155} 104. 0.374 (+/-0.103) for {'alpha': 0.7885372992905638} 105. 0.348 (+/-0.102) for {'alpha': 0.9208527728773261} 106. 0.314 (+/-0.095) for {'alpha': 1.075370600831142} 107. 0.272 (+/-0.089) for {'alpha': 1.2558163076585396} 108. 0.212 (+/-0.084) for {'alpha': 1.466540555750942} 109. 0.129 (+/-0.087) for {'alpha': 1.7126240426614014} 110. 0.018 (+/-0.098) for {'alpha': 2.0} 111. m_log_alphas: 100 [-0.77418297 -0.70440767 -0.63463236 -0.56485706 -0.49508175 -0.42530644 112. -0.35553114 -0.28575583 -0.21598053 -0.14620522 -0.07642991 -0.00665461 113. 0.0631207 0.132896 0.20267131 0.27244662 0.34222192 0.41199723 114. 0.48177253 0.55154784 0.62132314 0.69109845 0.76087376 0.83064906 115. 0.90042437 0.97019967 1.03997498 1.10975029 1.17952559 1.2493009 116. 1.3190762 1.38885151 1.45862681 1.52840212 1.59817743 1.66795273 117. 1.73772804 1.80750334 1.87727865 1.94705396 2.01682926 2.08660457 118. 2.15637987 2.22615518 2.29593048 2.36570579 2.4354811 2.5052564 119. 2.57503171 2.64480701 2.71458232 2.78435763 2.85413293 2.92390824 120. 2.99368354 3.06345885 3.13323415 3.20300946 3.27278477 3.34256007 121. 3.41233538 3.48211068 3.55188599 3.6216613 3.6914366 3.76121191 122. 3.83098721 3.90076252 3.97053783 4.04031313 4.11008844 4.17986374 123. 4.24963905 4.31941435 4.38918966 4.45896497 4.52874027 4.59851558 124. 4.66829088 4.73806619 4.8078415 4.8776168 4.94739211 5.01716741 125. 5.08694272 5.15671802 5.22649333 5.29626864 5.36604394 5.43581925 126. 5.50559455 5.57536986 5.64514517 5.71492047 5.78469578 5.85447108 127. 5.92424639 5.99402169 6.063797 6.13357231] 128. 交叉验证选择的alpha: 0.06176875494949271 129. (100, 10) (100,) 130. alphas: 50 [1.00000000e-04 1.22398508e-04 1.49813947e-04 1.83370035e-04 131. 2.24442186e-04 2.74713886e-04 3.36245696e-04 4.11559714e-04 132. 5.03742947e-04 6.16573850e-04 7.54677190e-04 9.23713617e-04 133. 1.13061168e-03 1.38385182e-03 1.69381398e-03 2.07320303e-03 134. 2.53756957e-03 3.10594728e-03 3.80163312e-03 4.65314220e-03 135. 5.69537661e-03 6.97105597e-03 8.53246847e-03 1.04436141e-02 136. 1.27828277e-02 1.56459904e-02 1.91504587e-02 2.34398757e-02 137. 2.86900580e-02 3.51162028e-02 4.29817081e-02 5.26089693e-02 138. 6.43925932e-02 7.88155731e-02 9.64690852e-02 1.18076721e-01 139. 1.44524144e-01 1.76895395e-01 2.16517323e-01 2.65013972e-01 140. 3.24373147e-01 3.97027891e-01 4.85956213e-01 5.94803152e-01 141. 7.28030181e-01 8.91098077e-01 1.09069075e+00 1.33498920e+00 142. 1.63400685e+00 2.00000000e+00] 143. m_log_alphas: 50 [ 9.21034037 9.00822838 8.80611639 8.6040044 8.40189241 8.19978042 144. 7.99766843 7.79555644 7.59344445 7.39133245 7.18922046 6.98710847 145. 6.78499648 6.58288449 6.3807725 6.17866051 5.97654852 5.77443653 146. 5.57232454 5.37021255 5.16810055 4.96598856 4.76387657 4.56176458 147. 4.35965259 4.1575406 3.95542861 3.75331662 3.55120463 3.34909264 148. 3.14698065 2.94486866 2.74275666 2.54064467 2.33853268 2.13642069 149. 1.9343087 1.73219671 1.53008472 1.32797273 1.12586074 0.92374875 150. 0.72163676 0.51952476 0.31741277 0.11530078 -0.08681121 -0.2889232 151. -0.49103519 -0.69314718] 152. 交叉验证选择的alpha: 0.0046531422008170295
核心代码
1. class Ridge Found at: sklearn.linear_model._ridge 2. 3. class Ridge(MultiOutputMixin, RegressorMixin, _BaseRidge): 4. """Linear least squares with l2 regularization. 5. 6. Minimizes the objective function:: 7. 8. ||y - Xw||^2_2 + alpha * ||w||^2_2 9. 10. This model solves a regression model where the loss function is 11. the linear least squares function and regularization is given by 12. the l2-norm. Also known as Ridge Regression or Tikhonov regularization. 13. This estimator has built-in support for multi-variate regression 14. (i.e., when y is a 2d-array of shape (n_samples, n_targets)). 15. 16. Read more in the :ref:`User Guide <ridge_regression>`. 17. 18. Parameters 19. ---------- 20. alpha : {float, ndarray of shape (n_targets,)}, default=1.0 21. Regularization strength; must be a positive float. Regularization 22. improves the conditioning of the problem and reduces the variance of 23. the estimates. Larger values specify stronger regularization. 24. Alpha corresponds to ``1 / (2C)`` in other linear models such as 25. :class:`~sklearn.linear_model.LogisticRegression` or 26. :class:`sklearn.svm.LinearSVC`. If an array is passed, penalties are 27. assumed to be specific to the targets. Hence they must correspond in 28. number. 29. 30. fit_intercept : bool, default=True 31. Whether to fit the intercept for this model. If set 32. to false, no intercept will be used in calculations 33. (i.e. ``X`` and ``y`` are expected to be centered). 34. 35. normalize : bool, default=False 36. This parameter is ignored when ``fit_intercept`` is set to False. 37. If True, the regressors X will be normalized before regression by 38. subtracting the mean and dividing by the l2-norm. 39. If you wish to standardize, please use 40. :class:`sklearn.preprocessing.StandardScaler` before calling ``fit`` 41. on an estimator with ``normalize=False``. 42. 43. copy_X : bool, default=True 44. If True, X will be copied; else, it may be overwritten. 45. 46. max_iter : int, default=None 47. Maximum number of iterations for conjugate gradient solver. 48. For 'sparse_cg' and 'lsqr' solvers, the default value is determined 49. by scipy.sparse.linalg. For 'sag' solver, the default value is 1000. 50. 51. tol : float, default=1e-3 52. Precision of the solution. 53. 54. solver : {'auto', 'svd', 'cholesky', 'lsqr', 'sparse_cg', 'sag', 'saga'}, \ 55. default='auto' 56. Solver to use in the computational routines: 57. 58. - 'auto' chooses the solver automatically based on the type of data. 59. 60. - 'svd' uses a Singular Value Decomposition of X to compute the Ridge 61. coefficients. More stable for singular matrices than 'cholesky'. 62. 63. - 'cholesky' uses the standard scipy.linalg.solve function to 64. obtain a closed-form solution. 65. 66. - 'sparse_cg' uses the conjugate gradient solver as found in 67. scipy.sparse.linalg.cg. As an iterative algorithm, this solver is 68. more appropriate than 'cholesky' for large-scale data 69. (possibility to set `tol` and `max_iter`). 70. 71. - 'lsqr' uses the dedicated regularized least-squares routine 72. scipy.sparse.linalg.lsqr. It is the fastest and uses an iterative 73. procedure. 74. 75. - 'sag' uses a Stochastic Average Gradient descent, and 'saga' uses 76. its improved, unbiased version named SAGA. Both methods also use an 77. iterative procedure, and are often faster than other solvers when 78. both n_samples and n_features are large. Note that 'sag' and 79. 'saga' fast convergence is only guaranteed on features with 80. approximately the same scale. You can preprocess the data with a 81. scaler from sklearn.preprocessing. 82. 83. All last five solvers support both dense and sparse data. However, only 84. 'sag' and 'sparse_cg' supports sparse input when `fit_intercept` is 85. True. 86. 87. .. versionadded:: 0.17 88. Stochastic Average Gradient descent solver. 89. .. versionadded:: 0.19 90. SAGA solver. 91. 92. random_state : int, RandomState instance, default=None 93. Used when ``solver`` == 'sag' or 'saga' to shuffle the data. 94. See :term:`Glossary <random_state>` for details. 95. 96. .. versionadded:: 0.17 97. `random_state` to support Stochastic Average Gradient. 98. 99. Attributes 100. ---------- 101. coef_ : ndarray of shape (n_features,) or (n_targets, n_features) 102. Weight vector(s). 103. 104. intercept_ : float or ndarray of shape (n_targets,) 105. Independent term in decision function. Set to 0.0 if 106. ``fit_intercept = False``. 107. 108. n_iter_ : None or ndarray of shape (n_targets,) 109. Actual number of iterations for each target. Available only for 110. sag and lsqr solvers. Other solvers will return None. 111. 112. .. versionadded:: 0.17 113. 114. See also 115. -------- 116. RidgeClassifier : Ridge classifier 117. RidgeCV : Ridge regression with built-in cross validation 118. :class:`sklearn.kernel_ridge.KernelRidge` : Kernel ridge regression 119. combines ridge regression with the kernel trick 120. 121. Examples 122. -------- 123. >>> from sklearn.linear_model import Ridge 124. >>> import numpy as np 125. >>> n_samples, n_features = 10, 5 126. >>> rng = np.random.RandomState(0) 127. >>> y = rng.randn(n_samples) 128. >>> X = rng.randn(n_samples, n_features) 129. >>> clf = Ridge(alpha=1.0) 130. >>> clf.fit(X, y) 131. Ridge() 132. """ 133. @_deprecate_positional_args 134. def __init__(self, alpha=1.0, *, fit_intercept=True, normalize=False, 135. copy_X=True, max_iter=None, tol=1e-3, solver="auto", 136. random_state=None): 137. super().__init__(alpha=alpha, fit_intercept=fit_intercept, 138. normalize=normalize, copy_X=copy_X, max_iter=max_iter, tol=tol, 139. solver=solver, random_state=random_state) 140. 141. def fit(self, X, y, sample_weight=None): 142. """Fit Ridge regression model. 143. 144. Parameters 145. ---------- 146. X : {ndarray, sparse matrix} of shape (n_samples, n_features) 147. Training data 148. 149. y : ndarray of shape (n_samples,) or (n_samples, n_targets) 150. Target values 151. 152. sample_weight : float or ndarray of shape (n_samples,), default=None 153. Individual weights for each sample. If given a float, every sample 154. will have the same weight. 155. 156. Returns 157. ------- 158. self : returns an instance of self. 159. """ 160. return super().fit(X, y, sample_weight=sample_weight)