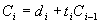1.ALU
算术逻辑单元(ALU)是专门执行算术和逻辑运算的数字电路。ALU是计算机中央处理器的最重要组成部分,甚至连最小的微处理器也包含ALU作计数功能。在现代CPU和GPU处理器中已含有功能强大和复杂的ALU;一个单一的元件也可能含有ALU。
ALU在CPU中的位置如下(百度上看到的图):
2.ALU的结构:
ALU的大致结构如下:
控制信号是由控制单元(CU)传过来的信息,CU:
控制单元(CU)负责解释指令、处理各种计算操作以及处理器和内存之间的数据传输。 它从内存中获取指令,将其解码并发送给其他部件执行,通俗来讲CU在这里的功能就是告诉ALU这是一个加,减,乘,除运算,还是某种逻辑运算的指令。
那么以74181为例:
74181有两种工作方式:正逻辑和负逻辑
正逻辑: 用高电平表示逻辑1,低电平表示逻辑0。
负逻辑:用高电平表示逻辑0,低电平表示逻辑1。
我们以正逻辑为例:
B3~B0和A3~A0是两个操作数(输入信号)
F3~F0为输出结果
C−1𝐶−1表示最低位的外来进位,Cn+4𝐶𝑛+4是74181向高位的进位
P、G可供先行进位(并行进位)使用:
由于串行进位的延迟时间太长,因为串行进位的每一级进位都是依赖于前一级的。
(比如C1 = G1+P1C0,C2 = G2 + P2C1,在这里C2是依赖于C1的,下面会讲)
所以出现了并行进位:其特点是各级进位信号同时形成。
比如:C1 = G1+P1C0,C2 = G1+P2G1+P2P1C0
C1和C2都是同时产生的,因为它们都只依赖于C0,C0同时打入,C1和C2就同时产生。
但是随着加法器位数不断增加,Ci的表达式会越来越长,这会使电路变得很复杂,所以完全采用并行进位是不现实的。
5个控制端:S0~S3,M
M用于区别算术运算还是逻辑运算;
S3~S0的不同取值可实现不同的运算。
当M=1,S3~S0=0110时,74181作逻辑运算A⊕B;
当M=0,S3~S0=0110时,74181作算术运算。
由上表可见,在正逻辑条件下,M=0,S3~S0=0110,且C−1=1时,完成A减B减1的操作。若想完成A减B运算,可使C−1=0。需注意,74181算术运算是用补码实现的,其中减数的反码是由内部电路形成的,而末位加“1”,则通过C−1=0来体现。
ALU为组合逻辑电路,因此实际应用ALU时,其输入端口A和B必须与锁存器相连,而且在运算的过程中锁存器的内容是不变的。其输出也必须送至寄存器中保存。
3.一位全加器
这是一个简单的加法运算:
其中的输出:Si=Ai⨁Bi⨁Ci+1(输入中有奇数个1时为1,那么进行异或就可以了)
想高位的进位(就是图中小的数字部分):输入中至少2个1,就向高位进位
Ci=AiBi+(Ai⨁Bi)Ci−1𝐴𝑖𝐵𝑖+(𝐴𝑖⨁𝐵𝑖)𝐶𝑖−1
两种情况相或:
AiBi
𝐴
𝑖
𝐵
𝑖
:两个输入都是1,那么这种情况下无论C=0还是1,都需要向高位进位
(Ai⨁Bi)Ci−1:两个输入中有一个位时1,且来自低位的进位Ci−1是1
最后得到的电路图如下:
如果屏蔽电路内部的一些细节,那么就可以得到全加器的结构:
4.串行加法器
只有一个全加器,数据逐位串行送入加法器中进行运算。进位触发器用来寄存进位信号,以便参与下一次运算。如果操作数长n位,加法就要分n次进行,每次产生一位和,并且串行逐位地送回寄存器。串行加法器加入了进位触发器,用来保存“进位位”:
例如,最开始时:
Ai=1,Bi=0,Ci−1𝐶𝑖−1=0,Si=1,那么我们可以确定进位是0,那么这个“0”就会保存在进位触发器中
5.并行加法器
并行加法器由若干个全加器组成,如下图所示。n+1个全加器级联,就组成了一个n+1位的并行加法器。
由下图可知,由于每位全加器的进位输出是高一位全加器的进位输入,因此当全加器有进位时,这种一级一级传递进位的过程,将会大大影响运算速度。
Ci进位有两部分组成:本地进位AiBi,可记作di,与低位无关;传递进位 (Ai⨁Bi)Ci−1 与低位有关;可称 Ai+Bi 为传递条件,记作ti,则:
由Ci的组成可以将逐级传递进位的结构,转换为以进位链的方式实现快速进位。目前进位链通常采用串行和并行两种:
串行进位链:
串行进位链是指并行加法器中的进位信号采用串行传递。以四位并行加法器为例,每一位的进位表达式可示为:
由上式可见,采用与非逻辑电路可方便地实现进位传递,如下图所示:
若设与非门的级延迟时间为ty,那么当di、ti形成后,共需8ty使可产生最高位的进位。实际上每增加一位全加器,进位时间就会增加2ty。n位全加器的最长进位时间为2nty。
并行进位链:
并行进位链是指并行加法器中的进位信号是同时产生的,又称先行进位、跳跃进位等。理想的并行进位链是n位全加器的n位进位同时产生,但实际实现有困难;通常并行进位链有单重分组和双重分组两种实现方案。
(1)单重分组跳跃进位。单重分组跳跃进位就是将M位全加器分成若干小组,小组内的进位同时产生,小组与小组之间采用串行进位,这种进位又有组内并行、组间串行之称。
以四位并行加法器为例,对其进位表示式稍作变换,便可获得并行进位表达式:
可得与其对应的逻辑图。如下图所示:
设与或非门的级延迟时间为1.5ty,如与非门的级延迟时间仍为1ty,则di、ti形成后,只需2.5ty就可产生全部进位。
如果将16位的全加器按四位一组分组,便可得单重分组跳跃进位链框图,如下图所示。
不难理解在di、ti形成后,经2.5ty可产生C3、C2、C3、C3四个进位信息,经10ty就可产生全部进位,而n=16的串行进位链的全部进位时间为32ty,可见单重分组方案进位时间仅为串行进位链的三分之一。
但随着n的增大,其优势便很快减弱,如当n=64时,按4位分组,共为16组,组间有16位串行进位,在di、ti形成后,还需经40ty才能产生全部进位,显然进位时间太长。如果能使组间进位也同时产生,必然会更大地提高进位速度,这就是组内、组间均为并行进位的方案。
(2)双重分组跳跃进位。双重分组跳跃进位就是将n位全加器分成几个大组,每个大组又包含几个小组,而每个大组内所包含的各个小组的最高位进位是同时形成的,大组与大组间采用串行进位。因各小组最高位进位是同时形成的,小组内的其他进位也是同时形成的(注意两小组内的其他进位与小组的最高位进位并不是同时产生的),故又有组(小组)内并行、组(小组)间并行之称。下图是一个32位并行加法器双重分组跳跃进位链的框图。
图中共分两大组,每个大组内包含4个小组,第一大组内的4个小组的最高位进位C31、C27、C23、C19是同时产生的;第二大组内4个小组的最高位进位C15、C11、C7、C3也是同时产生的,而第二大组向第一大组的进位C15采用串行进位方式。