Sklearn、TensorFlow 与 Keras 机器学习实用指南第三版（八）（1）

第十八章：强化学习

强化学习（RL）是当今最激动人心的机器学习领域之一，也是最古老的之一。自上世纪 50 年代以来一直存在，多年来产生了许多有趣的应用，特别是在游戏（例如 TD-Gammon，一个下棋程序）和机器控制方面，但很少成为头条新闻。然而，一场革命发生在2013 年，当时来自英国初创公司 DeepMind 的研究人员展示了一个系统，可以从头开始学习玩几乎任何 Atari 游戏，最终在大多数游戏中超越人类，只使用原始像素作为输入，而不需要任何关于游戏规则的先验知识。这是一系列惊人壮举的开始，最终在 2016 年 3 月，他们的系统 AlphaGo 在围棋比赛中击败了传奇职业选手李世石，并在 2017 年 5 月击败了世界冠军柯洁。没有任何程序曾经接近击败这个游戏的大师，更不用说世界冠军了。如今，整个强化学习领域充满了新的想法，具有广泛的应用范围。

那么，DeepMind（2014 年被 Google 以超过 5 亿美元的价格收购）是如何实现所有这些的呢？回顾起来似乎相当简单：他们将深度学习的力量应用于强化学习领域，而且效果超出了他们最疯狂的梦想。在本章中，我将首先解释什么是强化学习以及它擅长什么，然后介绍深度强化学习中最重要的两种技术：策略梯度和深度 Q 网络，包括对马尔可夫决策过程的讨论。让我们开始吧！

学习优化奖励

在强化学习中，软件 代理 在一个 环境 中进行 观察 和 行动，并从环境中获得 奖励。其目标是学会以一种方式行动，以最大化其随时间的预期奖励。如果您不介意有点拟人化，您可以将积极奖励视为快乐，将负面奖励视为痛苦（在这种情况下，“奖励”这个术语有点误导）。简而言之，代理在环境中行动，并通过试错学习来最大化其快乐并最小化其痛苦。

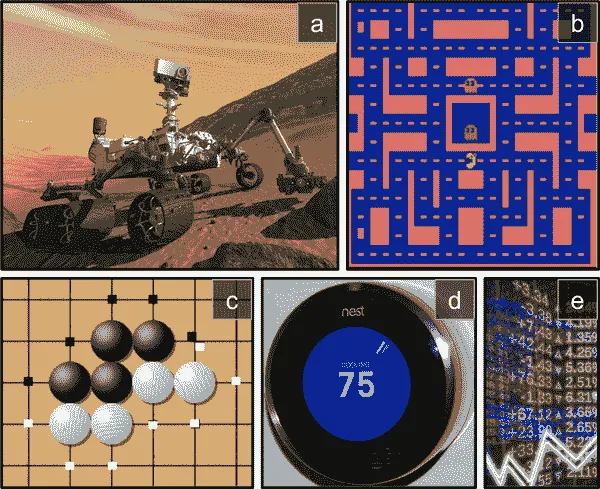
这是一个非常广泛的设置，可以应用于各种任务。以下是一些示例（参见 图 18-1）：

1. 代理程序可以是控制机器人的程序。在这种情况下，环境是真实世界，代理通过一组传感器（如摄像头和触摸传感器）观察环境，其行动包括发送信号以激活电机。它可能被编程为在接近目标位置时获得积极奖励，而在浪费时间或走错方向时获得负面奖励。
   
2. 代理可以是控制 Ms. Pac-Man 的程序。在这种情况下，环境是 Atari 游戏的模拟，行动是九种可能的摇杆位置（左上、下、中心等），观察是屏幕截图，奖励只是游戏得分。
   
3. 同样，代理可以是玩围棋等棋盘游戏的程序。只有在赢得比赛时才会获得奖励。
   
4. 代理不必控制物理（或虚拟）移动的东西。例如，它可以是一个智能恒温器，每当接近目标温度并节省能源时获得积极奖励，当人类需要调整温度时获得负面奖励，因此代理必须学会预测人类需求。
   
5. 代理可以观察股市价格并决定每秒买入或卖出多少。奖励显然是货币收益和损失。
   

请注意，可能根本没有任何正面奖励；例如，代理可能在迷宫中四处移动，在每个时间步都会获得负面奖励，因此最好尽快找到出口！还有许多其他适合强化学习的任务示例，例如自动驾驶汽车、推荐系统、在网页上放置广告，或者控制图像分类系统应该关注的位置。

图 18-1. 强化学习示例：(a) 机器人，(b) Ms. Pac-Man，© 围棋选手，(d) 恒温器，(e) 自动交易员⁠⁵

策略搜索

软件代理用来确定其行动的算法称为其策略。策略可以是一个神经网络，将观察作为输入并输出要采取的行动（见图 18-2）。

图 18-2。使用神经网络策略的强化学习

策略可以是你能想到的任何算法，并且不必是确定性的。实际上，在某些情况下，它甚至不必观察环境！例如，考虑一个机器人吸尘器，其奖励是在 30 分钟内吸尘的量。它的策略可以是每秒以概率p向前移动，或者以概率 1 - p随机向左或向右旋转。旋转角度将是- r和+ r之间的随机角度。由于这个策略涉及一些随机性，它被称为随机策略。机器人将有一个不规则的轨迹，这保证了它最终会到达它可以到达的任何地方并清理所有的灰尘。问题是，在 30 分钟内它会吸尘多少？

你会如何训练这样的机器人？你只能调整两个策略参数：概率p和角度范围r。一个可能的学习算法是尝试许多不同的参数值，并选择表现最好的组合（参见图 18-3）。这是一个策略搜索的例子，这种情况下使用了一种蛮力方法。当策略空间太大时（这通常是情况），通过这种方式找到一组好的参数就像在一个巨大的草堆中寻找一根针。

探索政策空间的另一种方法是使用遗传算法。例如，您可以随机创建第一代 100 个政策并尝试它们，然后“淘汰”最差的 80 个政策，并让 20 个幸存者每人产生 4 个后代。后代是其父母的副本加上一些随机变化。幸存的政策及其后代一起构成第二代。您可以继续通过这种方式迭代生成，直到找到一个好的政策。

图 18-3。政策空间中的四个点（左）和代理的相应行为（右）

另一种方法是使用优化技术，通过评估奖励相对于策略参数的梯度，然后通过沿着梯度朝着更高奖励的方向调整这些参数。我们将在本章后面更详细地讨论这种方法，称为策略梯度（PG）。回到吸尘器机器人，您可以稍微增加p，并评估这样做是否会增加机器人在 30 分钟内吸尘的量；如果是，那么再增加p一些，否则减少p。我们将使用 TensorFlow 实现一个流行的 PG 算法，但在此之前，我们需要为代理创建一个环境——现在是介绍 OpenAI Gym 的时候了。

OpenAI Gym 简介

强化学习的一个挑战是，为了训练一个代理程序，您首先需要一个可用的环境。如果您想编写一个代理程序来学习玩 Atari 游戏，您将需要一个 Atari 游戏模拟器。如果您想编写一个行走机器人，那么环境就是现实世界，您可以直接在该环境中训练您的机器人。然而，这也有其局限性：如果机器人掉下悬崖，您不能简单地点击撤销。您也不能加快时间——增加计算能力不会使机器人移动得更快——而且通常来说，同时训练 1000 个机器人的成本太高。简而言之，在现实世界中训练是困难且缓慢的，因此您通常至少需要一个模拟环境来进行引导训练。例如，您可以使用类似PyBullet或MuJoCo的库进行 3D 物理模拟。

OpenAI Gym是一个工具包，提供各种模拟环境（Atari 游戏，棋盘游戏，2D 和 3D 物理模拟等），您可以用它来训练代理程序，比较它们，或者开发新的 RL 算法。

OpenAI Gym 在 Colab 上预先安装，但是它是一个较旧的版本，因此您需要用最新版本替换它。您还需要安装一些它的依赖项。如果您在自己的机器上编程而不是在 Colab 上，并且按照https://homl.info/install上的安装说明进行操作，那么您可以跳过这一步；否则，请输入以下命令：

# Only run these commands on Colab or Kaggle!
%pip install -q -U gym
%pip install -q -U gym[classic_control,box2d,atari,accept-rom-license]

第一个%pip命令将 Gym 升级到最新版本。-q选项代表quiet：它使输出更简洁。-U选项代表upgrade。第二个%pip命令安装了运行各种环境所需的库。这包括来自控制理论（控制动态系统的科学）的经典环境，例如在小车上平衡杆。它还包括基于 Box2D 库的环境——一个用于游戏的 2D 物理引擎。最后，它包括基于 Arcade Learning Environment（ALE）的环境，这是 Atari 2600 游戏的模拟器。几个 Atari 游戏的 ROM 会被自动下载，通过运行这段代码，您同意 Atari 的 ROM 许可证。

有了这个，您就可以使用 OpenAI Gym 了。让我们导入它并创建一个环境：

import gym
env = gym.make("CartPole-v1", render_mode="rgb_array")

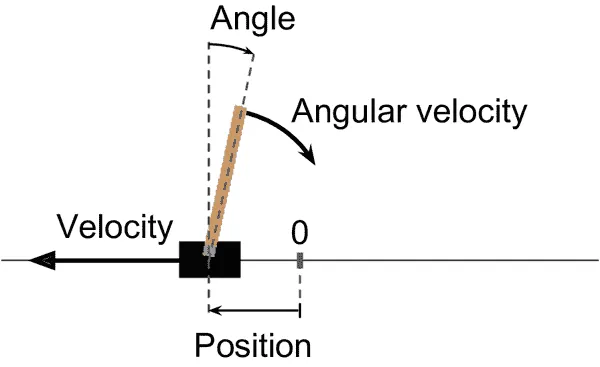
在这里，我们创建了一个 CartPole 环境。这是一个 2D 模拟，其中一个小车可以被加速向左或向右，以平衡放在其顶部的杆（参见图 18-4）。这是一个经典的控制任务。

提示

gym.envs.registry字典包含所有可用环境的名称和规格。

图 18-4。CartPole 环境

在创建环境之后，您必须使用reset()方法对其进行初始化，可以选择性地指定一个随机种子。这将返回第一个观察结果。观察结果取决于环境的类型。对于 CartPole 环境，每个观察结果都是一个包含四个浮点数的 1D NumPy 数组，表示小车的水平位置（0.0 = 中心），其速度（正数表示向右），杆的角度（0.0 = 垂直），以及其角速度（正数表示顺时针）。reset()方法还返回一个可能包含额外环境特定信息的字典。这对于调试或训练可能很有用。例如，在许多 Atari 环境中，它包含剩余的生命次数。然而，在 CartPole 环境中，这个字典是空的。

>>> obs, info = env.reset(seed=42)
>>> obs
array([ 0.0273956 , -0.00611216,  0.03585979,  0.0197368 ], dtype=float32)
>>> info
{}

让我们调用render()方法将这个环境渲染为图像。由于在创建环境时设置了render_mode="rgb_array"，图像将作为一个 NumPy 数组返回：

>>> img = env.render()
>>> img.shape  # height, width, channels (3 = Red, Green, Blue)
(400, 600, 3)

然后，您可以使用 Matplotlib 的imshow()函数来显示这个图像，就像往常一样。

现在让我们询问环境有哪些可能的动作：

>>> env.action_space
Discrete(2)

Discrete(2)表示可能的动作是整数 0 和 1，分别代表向左或向右加速。其他环境可能有额外的离散动作，或其他类型的动作（例如连续动作）。由于杆向右倾斜（obs[2] > 0），让我们加速小车向右：

>>> action = 1  # accelerate right
>>> obs, reward, done, truncated, info = env.step(action)
>>> obs
array([ 0.02727336,  0.18847767,  0.03625453, -0.26141977], dtype=float32)
>>> reward
1.0
>>> done
False
>>> truncated
False
>>> info
{}

step() 方法执行所需的动作并返回五个值：

obs

这是新的观察。小车现在向右移动（obs[1] > 0）。杆仍然向右倾斜（obs[2] > 0），但它的角速度现在是负的（obs[3] < 0），所以在下一步之后它可能会向左倾斜。

reward

在这个环境中，无论你做什么，每一步都会获得 1.0 的奖励，所以目标是尽可能让情节运行更长时间。

done

当情节结束时，这个值将是True。当杆倾斜得太多，或者离开屏幕，或者经过 200 步后（在这种情况下，你赢了），情节就会结束。之后，环境必须被重置才能再次使用。

truncated

当一个情节被提前中断时，这个值将是True，例如通过一个强加每个情节最大步数的环境包装器（请参阅 Gym 的文档以获取有关环境包装器的更多详细信息）。一些强化学习算法会将截断的情节与正常结束的情节（即done为True时）区别对待，但在本章中，我们将对它们进行相同处理。

info

这个特定于环境的字典可能提供额外的信息，就像reset()方法返回的那样。

提示

当你使用完一个环境后，应该调用它的close()方法来释放资源。

让我们硬编码一个简单的策略，当杆向左倾斜时加速向左，当杆向右倾斜时加速向右。我们将运行此策略，以查看它在 500 个情节中获得的平均奖励：

def basic_policy(obs):
    angle = obs[2]
    return 0 if angle < 0 else 1
totals = []
for episode in range(500):
    episode_rewards = 0
    obs, info = env.reset(seed=episode)
    for step in range(200):
        action = basic_policy(obs)
        obs, reward, done, truncated, info = env.step(action)
        episode_rewards += reward
        if done or truncated:
            break
    totals.append(episode_rewards)

这段代码是不言自明的。让我们看看结果：

>>> import numpy as np
>>> np.mean(totals), np.std(totals), min(totals), max(totals)
(41.698, 8.389445512070509, 24.0, 63.0)

即使尝试了 500 次，这个策略也从未成功让杆连续保持直立超过 63 步。不太好。如果你看一下本章笔记本中的模拟，你会看到小车左右摆动得越来越强烈，直到杆倾斜得太多。让我们看看神经网络是否能提出一个更好的策略。

神经网络策略

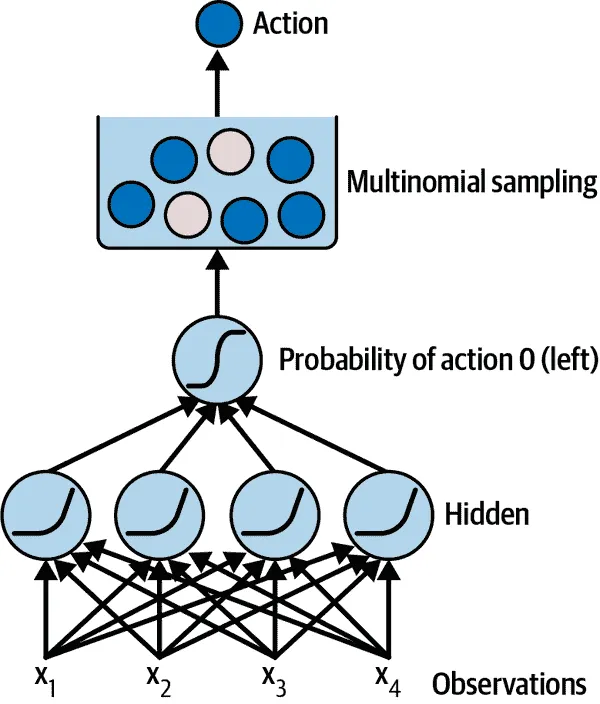
让我们创建一个神经网络策略。这个神经网络将以观察作为输入，并输出要执行的动作，就像我们之前硬编码的策略一样。更准确地说，它将为每个动作估计一个概率，然后我们将根据估计的概率随机选择一个动作（参见图 18-5）。在 CartPole 环境中，只有两种可能的动作（左或右），所以我们只需要一个输出神经元。它将输出动作 0（左）的概率p，当然动作 1（右）的概率将是 1 - p。例如，如果它输出 0.7，那么我们将以 70%的概率选择动作 0，或者以 30%的概率选择动作 1。

图 18-5. 神经网络策略

你可能会想为什么我们根据神经网络给出的概率随机选择一个动作，而不是只选择得分最高的动作。这种方法让代理人在探索新动作和利用已知效果良好的动作之间找到平衡。这里有一个类比：假设你第一次去一家餐馆，所有菜看起来都一样吸引人，所以你随机挑选了一个。如果它很好吃，你可以增加下次点它的概率，但你不应该将这个概率增加到 100%，否则你永远不会尝试其他菜，其中一些可能比你尝试的这个更好。这个探索/利用的困境在强化学习中是核心的。

还要注意，在这种特定环境中，过去的动作和观察可以安全地被忽略，因为每个观察包含了环境的完整状态。如果有一些隐藏状态，那么您可能需要考虑过去的动作和观察。例如，如果环境只透露了小车的位置而没有速度，那么您不仅需要考虑当前观察，还需要考虑上一个观察以估计当前速度。另一个例子是当观察是嘈杂的；在这种情况下，通常希望使用过去几个观察来估计最可能的当前状态。因此，CartPole 问题非常简单；观察是无噪声的，并且包含了环境的完整状态。

以下是使用 Keras 构建基本神经网络策略的代码：

import tensorflow as tf
model = tf.keras.Sequential([
    tf.keras.layers.Dense(5, activation="relu"),
    tf.keras.layers.Dense(1, activation="sigmoid"),
])

我们使用Sequential模型来定义策略网络。输入的数量是观察空间的大小——在 CartPole 的情况下是 4——我们只有五个隐藏单元，因为这是一个相当简单的任务。最后，我们希望输出一个单一的概率——向左移动的概率——因此我们使用具有 sigmoid 激活函数的单个输出神经元。如果有超过两种可能的动作，每种动作将有一个输出神经元，并且我们将使用 softmax 激活函数。

好的，现在我们有一个神经网络策略，它将接收观察并输出动作概率。但是我们如何训练它呢？

评估动作：信用分配问题

如果我们知道每一步的最佳行动是什么，我们可以像平常一样训练神经网络，通过最小化估计概率分布与目标概率分布之间的交叉熵来实现，这将只是常规的监督学习。然而，在强化学习中，智能体得到的唯一指导是通过奖励，而奖励通常是稀疏和延迟的。例如，如果智能体设法在 100 步内平衡杆，它如何知道这 100 个动作中哪些是好的，哪些是坏的？它只知道在最后一个动作之后杆倒了，但肯定不是这个最后一个动作完全负责。这被称为信用分配问题：当智能体获得奖励时，它很难知道哪些动作应该得到赞扬（或责备）。想象一只狗表现良好几个小时后才得到奖励；它会明白为什么会得到奖励吗？

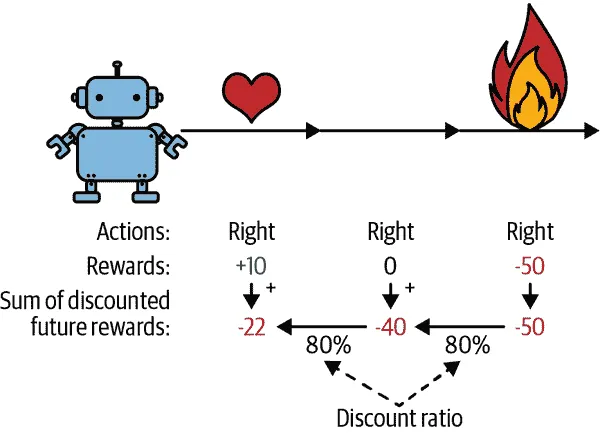
为了解决这个问题，一个常见的策略是基于之后所有奖励的总和来评估一个动作，通常在每一步应用一个折扣因子，γ（gamma）。这些折扣后的奖励之和被称为动作的回报。考虑图 18-6 中的例子。如果一个智能体连续三次向右移动，并在第一步后获得+10 奖励，在第二步后获得 0 奖励，最后在第三步后获得-50 奖励，那么假设我们使用一个折扣因子γ=0.8，第一个动作的回报将是 10 + γ × 0 + γ² × (–50) = –22。如果折扣因子接近 0，那么未来的奖励与即时奖励相比不会占据很大比重。相反，如果折扣因子接近 1，那么未来的奖励将几乎和即时奖励一样重要。典型的折扣因子从 0.9 到 0.99 不等。使用折扣因子 0.95，未来 13 步的奖励大约相当于即时奖励的一半（因为 0.95¹³ ≈ 0.5），而使用折扣因子 0.99，未来 69 步的奖励相当于即时奖励的一半。在 CartPole 环境中，动作具有相当短期的影响，因此选择折扣因子 0.95 似乎是合理的。

图 18-6。计算动作的回报：折扣未来奖励之和

当然，一个好的行动可能会被几个导致杆迅速倒下的坏行动跟随，导致好的行动获得较低的回报。同样，一个好的演员有时可能会出演一部糟糕的电影。然而，如果我们玩足够多次游戏，平均而言好的行动将获得比坏行动更高的回报。我们想要估计一个行动相对于其他可能行动的平均优势有多大。这被称为行动优势。为此，我们必须运行许多情节，并通过减去均值并除以标准差来标准化所有行动回报。之后，我们可以合理地假设具有负优势的行动是坏的，而具有正优势的行动是好的。现在我们有了一种评估每个行动的方法，我们准备使用策略梯度来训练我们的第一个代理。让我们看看如何。

策略梯度

正如前面讨论的，PG 算法通过沿着梯度朝着更高奖励的方向优化策略的参数。一种流行的 PG 算法类别称为REINFORCE 算法，由 Ronald Williams 于 1992 年提出。这里是一个常见的变体：

1. 首先，让神经网络策略玩游戏多次，并在每一步计算使选择的行动更有可能的梯度，但暂时不应用这些梯度。
   
2. 在运行了几个情节之后，使用前一节中描述的方法计算每个行动的优势。
   
3. 如果一个行动的优势是正的，这意味着这个行动可能是好的，你希望应用之前计算的梯度，使这个行动在未来更有可能被选择。然而，如果一个行动的优势是负的，这意味着这个行动可能是坏的，你希望应用相反的梯度，使这个行动在未来略微减少。解决方案是将每个梯度向量乘以相应行动的优势。
   
4. 最后，计算所有结果梯度向量的平均值，并用它执行一步梯度下降。
   

让我们使用 Keras 来实现这个算法。我们将训练之前构建的神经网络策略，使其学会在小车上平衡杆。首先，我们需要一个函数来执行一步。我们暂时假设无论采取什么行动都是正确的，以便我们可以计算损失及其梯度。这些梯度将暂时保存一段时间，我们稍后会根据行动的好坏来修改它们：

def play_one_step(env, obs, model, loss_fn):
    with tf.GradientTape() as tape:
        left_proba = model(obs[np.newaxis])
        action = (tf.random.uniform([1, 1]) > left_proba)
        y_target = tf.constant([[1.]]) - tf.cast(action, tf.float32)
        loss = tf.reduce_mean(loss_fn(y_target, left_proba))
    grads = tape.gradient(loss, model.trainable_variables)
    obs, reward, done, truncated, info = env.step(int(action))
    return obs, reward, done, truncated, grads

让我们来看看这个函数：

• 在GradientTape块中（参见第十二章），我们首先调用模型，给它一个观察值。我们将观察值重塑为包含单个实例的批次，因为模型期望一个批次。这将输出向左移动的概率。
  
• 接下来，我们随机抽取一个介于 0 和 1 之间的浮点数，并检查它是否大于left_proba。action将以left_proba的概率为False，或以1 - left_proba的概率为True。一旦我们将这个布尔值转换为整数，行动将以适当的概率为 0（左）或 1（右）。
  
• 现在我们定义向左移动的目标概率：它是 1 减去行动（转换为浮点数）。如果行动是 0（左），那么向左移动的目标概率将是 1。如果行动是 1（右），那么目标概率将是 0。
  
• 然后我们使用给定的损失函数计算损失，并使用 tape 计算损失相对于模型可训练变量的梯度。同样，这些梯度稍后会在应用之前进行调整，取决于行动的好坏。
  
• 最后，我们执行选择的行动，并返回新的观察值、奖励、该情节是否结束、是否截断，当然还有我们刚刚计算的梯度。
  

现在让我们创建另一个函数，它将依赖于play_one_step()函数来玩多个回合，返回每个回合和每个步骤的所有奖励和梯度：

def play_multiple_episodes(env, n_episodes, n_max_steps, model, loss_fn):
    all_rewards = []
    all_grads = []
    for episode in range(n_episodes):
        current_rewards = []
        current_grads = []
        obs, info = env.reset()
        for step in range(n_max_steps):
            obs, reward, done, truncated, grads = play_one_step(
                env, obs, model, loss_fn)
            current_rewards.append(reward)
            current_grads.append(grads)
            if done or truncated:
                break
        all_rewards.append(current_rewards)
        all_grads.append(current_grads)
    return all_rewards, all_grads

这段代码返回了一个奖励列表的列表：每个回合一个奖励列表，每个步骤一个奖励。它还返回了一个梯度列表的列表：每个回合一个梯度列表，每个梯度列表包含每个步骤的一个梯度元组，每个元组包含每个可训练变量的一个梯度张量。

该算法将使用play_multiple_episodes()函数多次玩游戏（例如，10 次），然后它将回头查看所有奖励，对其进行折扣，并对其进行归一化。为此，我们需要几个额外的函数；第一个将计算每个步骤的未来折扣奖励总和，第二个将通过减去均值并除以标准差来对所有这些折扣奖励（即回报）在许多回合中进行归一化：

def discount_rewards(rewards, discount_factor):
    discounted = np.array(rewards)
    for step in range(len(rewards) - 2, -1, -1):
        discounted[step] += discounted[step + 1] * discount_factor
    return discounted
def discount_and_normalize_rewards(all_rewards, discount_factor):
    all_discounted_rewards = [discount_rewards(rewards, discount_factor)
                              for rewards in all_rewards]
    flat_rewards = np.concatenate(all_discounted_rewards)
    reward_mean = flat_rewards.mean()
    reward_std = flat_rewards.std()
    return [(discounted_rewards - reward_mean) / reward_std
            for discounted_rewards in all_discounted_rewards]

让我们检查一下这是否有效：

>>> discount_rewards([10, 0, -50], discount_factor=0.8)
array([-22, -40, -50])
>>> discount_and_normalize_rewards([[10, 0, -50], [10, 20]],
...                                discount_factor=0.8)
...
[array([-0.28435071, -0.86597718, -1.18910299]),
 array([1.26665318, 1.0727777 ])]

调用discount_rewards()返回了我们预期的结果（见图 18-6）。您可以验证函数discount_and_normalize_rewards()确实返回了两个回合中每个动作的归一化优势。请注意，第一个回合比第二个回合差得多，因此它的归一化优势都是负数；第一个回合的所有动作都被认为是不好的，反之第二个回合的所有动作都被认为是好的。

我们几乎准备好运行算法了！现在让我们定义超参数。我们将运行 150 次训练迭代，每次迭代玩 10 个回合，每个回合最多持续 200 步。我们将使用折扣因子 0.95：

n_iterations = 150
n_episodes_per_update = 10
n_max_steps = 200
discount_factor = 0.95

我们还需要一个优化器和损失函数。一个常规的 Nadam 优化器，学习率为 0.01，将会很好地完成任务，我们将使用二元交叉熵损失函数，因为我们正在训练一个二元分类器（有两种可能的动作——左或右）：

optimizer = tf.keras.optimizers.Nadam(learning_rate=0.01)
loss_fn = tf.keras.losses.binary_crossentropy

现在我们准备构建和运行训练循环！

for iteration in range(n_iterations):
    all_rewards, all_grads = play_multiple_episodes(
        env, n_episodes_per_update, n_max_steps, model, loss_fn)
    all_final_rewards = discount_and_normalize_rewards(all_rewards,
                                                       discount_factor)
    all_mean_grads = []
    for var_index in range(len(model.trainable_variables)):
        mean_grads = tf.reduce_mean(
            [final_reward * all_grads[episode_index][step][var_index]
             for episode_index, final_rewards in enumerate(all_final_rewards)
                 for step, final_reward in enumerate(final_rewards)], axis=0)
        all_mean_grads.append(mean_grads)
    optimizer.apply_gradients(zip(all_mean_grads, model.trainable_variables))

让我们逐步走过这段代码：

• 在每次训练迭代中，此循环调用play_multiple_episodes()函数，该函数播放 10 个回合，并返回每个步骤中每个回合的奖励和梯度。
  
• 然后我们调用discount_and_normalize_rewards()函数来计算每个动作的归一化优势，这在这段代码中称为final_reward。这提供了一个衡量每个动作实际上是好还是坏的指标。
  
• 接下来，我们遍历每个可训练变量，并对每个变量计算所有回合和所有步骤中该变量的梯度的加权平均，权重为final_reward。
  
• 最后，我们使用优化器应用这些均值梯度：模型的可训练变量将被微调，希望策略会有所改善。
  

我们完成了！这段代码将训练神经网络策略，并成功学会在小车上平衡杆。每个回合的平均奖励将非常接近 200。默认情况下，这是该环境的最大值。成功！

我们刚刚训练的简单策略梯度算法解决了 CartPole 任务，但是它在扩展到更大更复杂的任务时效果不佳。事实上，它具有很高的样本效率低，这意味着它需要很长时间探索游戏才能取得显著进展。这是因为它必须运行多个回合来估计每个动作的优势，正如我们所见。然而，它是更强大算法的基础，比如演员-评论家算法（我们将在本章末简要讨论）。

提示

研究人员试图找到即使代理最初对环境一无所知也能很好运行的算法。然而，除非你在写论文，否则不应该犹豫向代理注入先验知识，因为这将极大加快训练速度。例如，由于你知道杆应该尽可能垂直，你可以添加与杆角度成比例的负奖励。这将使奖励变得不那么稀疏，加快训练速度。此外，如果你已经有一个相当不错的策略（例如硬编码），你可能希望在使用策略梯度来改进之前，训练神经网络来模仿它。

现在我们将看一下另一个流行的算法家族。PG 算法直接尝试优化策略以增加奖励，而我们现在要探索的算法则不那么直接：代理学习估计每个状态的预期回报，或者每个状态中每个动作的预期回报，然后利用这些知识来决定如何行动。要理解这些算法，我们首先必须考虑马尔可夫决策过程（MDPs）。

马尔可夫决策过程

20 世纪初，数学家安德烈·马尔可夫研究了没有记忆的随机过程，称为马尔可夫链。这样的过程具有固定数量的状态，并且在每一步中随机从一个状态演变到另一个状态。它从状态s演变到状态s′的概率是固定的，仅取决于对(s, s′)这一对，而不取决于过去的状态。这就是为什么我们说该系统没有记忆。

图 18-7 显示了一个具有四个状态的马尔可夫链的示例。

图 18-7. 马尔可夫链示例

假设过程从状态s[0]开始，并且有 70%的概率在下一步保持在该状态。最终，它必定会离开该状态并永远不会回来，因为没有其他状态指向s[0]。如果它进入状态s[1]，那么它很可能会进入状态s[2]（90%的概率），然后立即返回到状态s[1]（100%的概率）。它可能在这两个状态之间交替多次，但最终会陷入状态s[3]并永远留在那里，因为没有出路：这被称为终止状态。马尔可夫链的动态可能非常不同，并且在热力学、化学、统计学等领域被广泛使用。

马尔可夫决策过程是在 20 世纪 50 年代由理查德·贝尔曼首次描述的。⁠¹² 它们类似于马尔可夫链，但有一个区别：在每一步中，代理可以选择几种可能的动作之一，转移概率取决于所选择的动作。此外，一些状态转移会产生一些奖励（正面或负面），代理的目标是找到一个能够随时间最大化奖励的策略。

例如，MDP 在图 18-8 中表示有三个状态（由圆圈表示），并且在每一步最多有三种可能的离散动作（由菱形表示）。

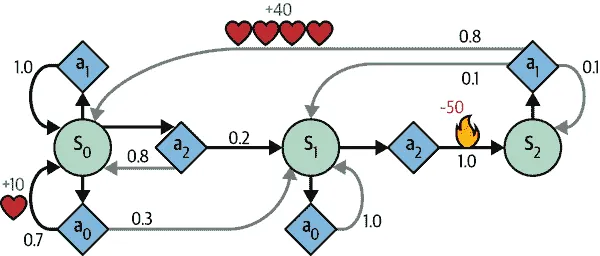
图 18-8. 马尔可夫决策过程示例

如果代理从状态 s[0] 开始，可以在行动 a[0]、a[1] 或 a[2] 之间选择。如果选择行动 a[1]，它就会肯定留在状态 s[0]，没有任何奖励。因此，如果愿意，它可以决定永远留在那里。但如果选择行动 a[0]，它有 70%的概率获得+10 的奖励并留在状态 s[0]。然后它可以一次又一次地尝试获得尽可能多的奖励，但最终会进入状态 s[1]。在状态 s[1] 中，它只有两种可能的行动：a[0] 或 a[2]。它可以通过反复选择行动 a[0] 来保持原地，或者选择移动到状态 s[2] 并获得-50 的负奖励（疼）。在状态 s[2] 中，它别无选择，只能采取行动 a[1]，这很可能会将其带回状态 s[0]，在途中获得+40 的奖励。你明白了。通过观察这个 MDP，你能猜出哪种策略会随着时间获得最多的奖励吗？在状态 s[0] 中，很明显行动 a[0] 是最佳选择，在状态 s[2] 中，代理别无选择，只能采取行动 a[1]，但在状态 s[1] 中，不明显代理应该保持原地（a[0]）还是冒险前进（a[2]）。

贝尔曼找到了一种估计任何状态 s 的最优状态值 V(s) 的方法，这是代理在到达该状态后可以期望的所有折扣未来奖励的总和，假设它采取最优行动。他表明，如果代理采取最优行动，那么贝尔曼最优性方程适用（参见方程 18-1）。这个递归方程表明，如果代理采取最优行动，那么当前状态的最优值等于在采取一个最优行动后平均获得的奖励，再加上这个行动可能导致的所有可能下一个状态的期望最优值。

方程 18-1. 贝尔曼最优性方程

V ( s ) = max a ∑ s‘ T ( s , a , s’ ) [ R ( s , a , s' ) + γ · V ( s' ) ] for all s

在这个方程中：

• T(s, a, s′) 是从状态 s 转移到状态 s′ 的转移概率，假设代理选择行动 a。例如，在图 18-8 中，T(s[2], a[1], s[0]) = 0.8。
  
• R(s, a, s′) 是代理从状态 s 转移到状态 s′ 时获得的奖励，假设代理选择行动 a。例如，在图 18-8 中，R(s[2], a[1], s[0]) = +40。
  
• γ 是折扣因子。
  

这个方程直接导致了一个算法，可以精确估计每个可能状态的最优状态值：首先将所有状态值估计初始化为零，然后使用值迭代算法进行迭代更新（参见方程 18-2）。一个显著的结果是，给定足够的时间，这些估计将收敛到最优状态值，对应于最优策略。

方程 18-2. 值迭代算法

V k+1 ( s ) ← max a ∑ s‘ T ( s , a , s’ ) [ R ( s , a , s‘ ) + γ · V k ( s’ ) ] for all s

在这个方程中，V**k是算法的第k次迭代中状态s的估计值。

注意

这个算法是动态规划的一个例子，它将一个复杂的问题分解成可迭代处理的可解子问题。

知道最优状态值可能很有用，特别是用于评估策略，但它并不能为代理提供最优策略。幸运的是，贝尔曼找到了一个非常相似的算法来估计最优状态-动作值，通常称为Q 值（质量值）。状态-动作对(s, a)的最优 Q 值，记为Q**(s, a)，是代理在到达状态s并选择动作a*后，在看到此动作结果之前，可以期望平均获得的折现未来奖励的总和，假设在此动作之后它表现最佳。

让我们看看它是如何工作的。再次，您首先将所有 Q 值的估计初始化为零，然后使用Q 值迭代算法进行更新（参见方程 18-3）。

方程 18-3。Q 值迭代算法

Q k+1 ( s , a ) ← ∑ s‘ T ( s , a , s’ ) [ R ( s , a , s‘ ) + γ · max a’ Q k ( s‘ , a’ ) ] for all ( s , a )

一旦您有了最优的 Q 值，定义最优策略π**(s)是微不足道的；当代理处于状态s时，它应该选择具有该状态最高 Q 值的动作：π(s)=argmaxaQ*(s,a)。

让我们将这个算法应用到图 18-8 中表示的 MDP 中。首先，我们需要定义 MDP：

transition_probabilities = [  # shape=[s, a, s']
    [[0.7, 0.3, 0.0], [1.0, 0.0, 0.0], [0.8, 0.2, 0.0]],
    [[0.0, 1.0, 0.0], None, [0.0, 0.0, 1.0]],
    [None, [0.8, 0.1, 0.1], None]
]
rewards = [  # shape=[s, a, s']
    [[+10, 0, 0], [0, 0, 0], [0, 0, 0]],
    [[0, 0, 0], [0, 0, 0], [0, 0, -50]],
    [[0, 0, 0], [+40, 0, 0], [0, 0, 0]]
]
possible_actions = [[0, 1, 2], [0, 2], [1]]

例如，要知道在执行动作a[1]后从s[2]到s[0]的转移概率，我们将查找transition_probabilities[2][1][0]（为 0.8）。类似地，要获得相应的奖励，我们将查找rewards[2][1][0]（为+40）。要获取s[2]中可能的动作列表，我们将查找possible_actions[2]（在这种情况下，只有动作a[1]是可能的）。接下来，我们必须将所有 Q 值初始化为零（对于不可能的动作，我们将 Q 值设置为-∞）：

Q_values = np.full((3, 3), -np.inf)  # -np.inf for impossible actions
for state, actions in enumerate(possible_actions):
    Q_values[state, actions] = 0.0  # for all possible actions

现在让我们运行 Q 值迭代算法。它重复应用方程 18-3，对每个状态和每个可能的动作的所有 Q 值进行计算：

gamma = 0.90  # the discount factor
for iteration in range(50):
    Q_prev = Q_values.copy()
    for s in range(3):
        for a in possible_actions[s]:
            Q_values[s, a] = np.sum([
                    transition_probabilities[s][a][sp]
                    * (rewards[s][a][sp] + gamma * Q_prev[sp].max())
                for sp in range(3)])

就是这样！得到的 Q 值看起来像这样：

>>> Q_values
array([[18.91891892, 17.02702702, 13.62162162],
 [ 0\.        ,        -inf, -4.87971488],
 [       -inf, 50.13365013,        -inf]])

例如，当代理处于状态s[0]并选择动作a[1]时，预期的折现未来奖励总和约为 17.0。

对于每个状态，我们可以找到具有最高 Q 值的动作：

>>> Q_values.argmax(axis=1)  # optimal action for each state
array([0, 0, 1])

这给出了在使用折扣因子为 0.90 时这个 MDP 的最优策略：在状态s[0]选择动作a[0]，在状态s[1]选择动作a[0]（即保持不动），在状态s[2]选择动作a[1]（唯一可能的动作）。有趣的是，如果将折扣因子增加到 0.95，最优策略会改变：在状态s[1]中，最佳动作变为a[2]（冲过火！）。这是有道理的，因为你越重视未来的奖励，你就越愿意忍受现在的一些痛苦，以换取未来的幸福。

时间差异学习

具有离散动作的强化学习问题通常可以建模为马尔可夫决策过程，但代理最初不知道转移概率是多少（它不知道T(s, a, s′)），也不知道奖励将会是什么（它不知道R(s, a, s′)）。它必须至少体验每个状态和每个转换一次才能知道奖励，如果要对转移概率有合理的估计，它必须多次体验它们。

时间差异（TD）学习算法与 Q 值迭代算法非常相似，但经过调整以考虑代理只有对 MDP 的部分知识这一事实。通常我们假设代理最初只知道可能的状态和动作，什么也不知道。代理使用一个探索策略——例如，一个纯随机策略——来探索 MDP，随着探索的进行，TD 学习算法根据实际观察到的转换和奖励更新状态值的估计（参见方程 18-4）。

方程 18-4. TD 学习算法

V k+1 (s)←(1-α) Vk (s)+α r+γ· Vk (s‘) 或者，等价地： Vk+1 (s)←Vk (s)+α· δk (s,r, s’) 其中δk (s,r,s′ )=r+γ · Vk (s')- Vk(s)

在这个方程中：

• α是学习率（例如，0.01）。
  
• r + γ · V**k被称为TD 目标。
  
• δk 被称为TD 误差。
  

写出这个方程的第一种形式的更简洁方法是使用符号a←αb，意思是a[k+1] ← (1 - α) · a[k] + α ·b[k]。因此，方程 18-4 的第一行可以重写为：V(s)←αr+γ·V(s')。

提示

TD 学习与随机梯度下降有许多相似之处，包括一次处理一个样本。此外，就像 SGD 一样，只有逐渐降低学习率，它才能真正收敛；否则，它将继续在最优 Q 值周围反弹。

对于每个状态s，该算法跟踪代理离开该状态后获得的即时奖励的平均值，以及它期望获得的奖励，假设它采取最优行动。

Sklearn、TensorFlow 与 Keras 机器学习实用指南第三版（八）（2）https://developer.aliyun.com/article/1482462