第一题
这道题目要注意的点是队伍的平均水平等于该队伍第二高水平,所以我们只需要让分出的几个队伍里第二高更大一点即可。
这道题我们只需要选择尽量打的两个数。可以借助排序来完成。
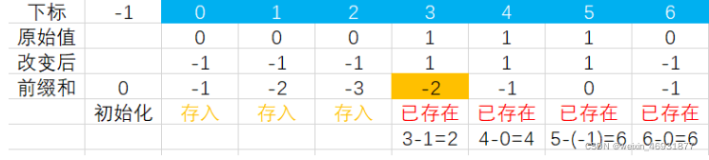
现在我们来观察取数的规律。来一个数据量更大的例子
一共有三组,第一组中间值下标为7,第二组下标为5,可以发现是依次减2的。有几组就循环几次。
加下来就可以根据逻辑写代码
#include <iostream> #include <vector> #include <algorithm> using namespace std; int main() { int num = 0; int ret = 0;//记录返回值 cin >> num; vector<int> score(3*num); for (int i = 0; i < 3 * num; i++) { cin >> score[i]; } sort(score.begin(), score.end()); for (int i = 0; i < num; i++) { ret += score[score.size() - 2 * (1 + i)]; } cout << ret; return 0; }
提交后发现有报错,这是因为我们定义的ret为int类型的,然而数据太大超出了int能表示的范围。
我们需要将int改为long就可以,再提交一遍。
第二题,进制转换
如果n大于9,对应数字参考16进制。
借助十进制来描述
在十进制以内我们还是可以轻松解决的,但是后边字母表示如何来实现呢?
我们可以借助一个字符数组
那二进制举一个例子
模拟上边的过程即可求出答案
#include <iostream> #include <string> #include <algorithm> using namespace std; int main() { int m, n; cin >> m >> n; string s = "0123456789ABCDEF"; string ret; while (m !=0) { ret=ret+s[m%n]; m /= n; } reverse(ret.begin(), ret.end()); cout << ret; return 0; }
运行后发现只会通过部分用例
这是因为我们忽略了0和负数的情况
所以我们要优化代码
#include <iostream> #include <string> #include <algorithm> using namespace std; int main() { int m, n; int flag=0; cin >> m >> n; if(m==0) { cout<<0; return 0; } else if(m<0) { m=0-m; flag=1; } string s = "0123456789ABCDEF"; string ret; while (m) { ret=ret+s[m%n]; m /= n; } if(flag==1) { ret+='-'; } reverse(ret.begin(), ret.end()); cout<<ret; return 0; }
第三题
这道题要我们求出最大的连续子串的和,是因为数组中含有负数。
如何找到子数组的最大和呢?
我们可以来模拟一下
我们可以模拟上边的过程
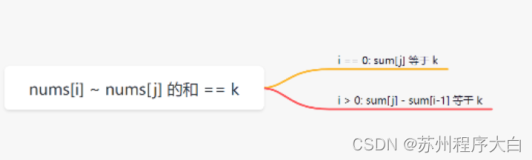
在第一次时,max的值初始化为5,定义一个sum。sum一直向后遍历,当sum为负数且遇到一个正数时,就将sum变换为当前遍历的值。
已经分析的很清晰了,接下来是代码呈现。
#include <iostream> #include <vector> using namespace std; int getMax(int a, int b){ return a>b? a:b; } int main(){ int num; cin >> num; vector<int> arr; arr.resize(num); for(int i=0; i<num; ++i){ cin >> arr[i]; } int sum = arr[0]; int maxSum = arr[0]; for(int i=1; i<num; ++i){ sum = getMax(arr[i], sum+arr[i]); if(sum > maxSum){ maxSum = sum; } } cout << maxSum; return 0; }
这道题的状态方程式为
可以看出这里类似于一个动态规划的问题,dp[i]就是以i结尾的子数组的和。