这里在啰嗦一下的是,在对链表操作的过程中,要时刻保证指针(有的语言称为引用)操作有效,避免无效操作。要做到这一点就要深刻理解指针的概念。另外,本篇中,所有的问题都是以单链表为例的,因为这些问题只有以单链表为情景时,才具有可分析性。
好了,本篇计划讲解以下5个例子。
- 1.链表反转
- 2.链表中环的检测
- 3.合并2个有序链表
- 4.查找链表的中间节点
- 5.查找链表中倒数第k个元素
本篇代码中,用到的单链表的节点定义如下
/// <summary> /// 单链表节点 /// </summary> public class SNode<T>where T:IComparable<T> { public T Value { get; set; } public SNode<T> Next { get; set; } public SNode(T val) { Value = val; } }
下面我们就开始进入正文。
链表反转
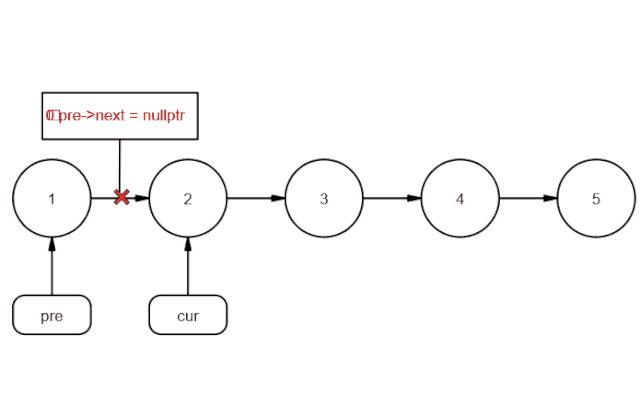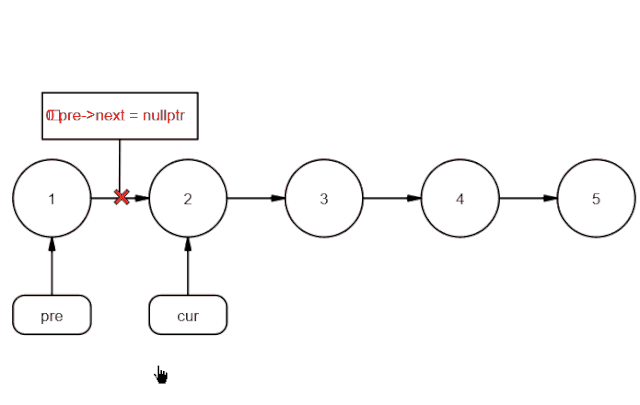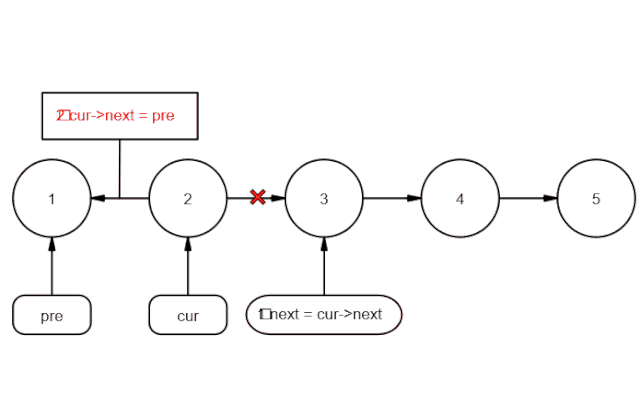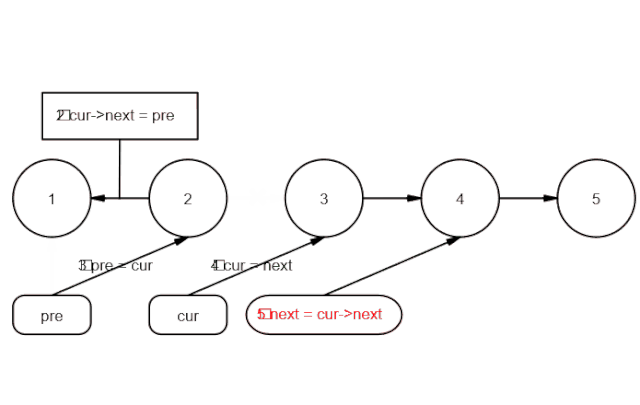
链表反转在面试中出现的概率非常之高,虽然最终实现相对也比较简单,但是,想要写出Bug free的代码却不是很容易,主要就是在指针的操作上容易出错,导致指针丢失,首先,我们先来看一下正常的解法思路。假设存在链表 1 → 2 → 3 → Ø,我们想要把它改成 Ø ← 1 ← 2 ← 3,对于单链表,我们只知道当前节点的下一个节点是谁,要想反转整个链表,正常来说,我们要考虑将当前节点的下一个节点,指向当前节点,依次循环,直到到达链表的末尾,可以结合下面的图片来理解一下。
现在,我们试着来理一下处理过程,我们可以借助3个指针来处理,用curNode指针指向当前的节点,next指向当前节点的下一节点,用指针pre指向当前节点的上一节点。当反转时,我们可以将curNode.next=pre,这样即完成了相邻的2个节点的反转,然后,将指针后移进行下一步操作即可。talk is cheap,下面给出代码,你可以结合看看。
//list是链表头结点 public SNode<T> Reverse(SNode<T> list) { SNode<T> prev = null; SNode<T> curNode = list; while (curNode != null) { SNode<T> node = curNode.Next; curNode.Next = prev; prev = curNode; curNode = node; } return prev; }
这种常规解法,我们再来看另一种解法思路。要反转链表,我们可以创建一个哨兵节点,然后遍历链表,将遍历到的元素依次插入到链表的第一个节点。即哨兵节点的下一个节点,这样,循环结束后,哨兵节点指向的节点即为反转后链表的头节点,如1-2-3-4-5 -->1-3-2-4-5 -->1-4-3-2-5 -->1-5-4-3-2 -->5-4-3-2-1,我们也称这种方法为头插法。下面来看一下代码。
public SNode<T> Reverse() { SNode<T> p, q; SNode<T> Head = new SNode<T>(default(T)); p = Head.Next; while (p.Next != null) { q = p.Next; p.Next = q.Next; q.Next = Head.Next; Head.Next = q; } p.Next = Head; Head = p.Next.Next; p.Next.Next = null; return Head; }
链表中环的检测
如果链表中有环,那如果用一个指针在链表上循环,则将一直循环下去,那如果我们用2个指针呢?如果用一快一慢两个指针来循环,若链表存在环,那么快慢指针终将会在环上相遇。这里用到的即是快慢指针的思想,有了这个思想,实现还是很简单的,我们来看下具体实现。
public bool HasCycle() { SNode<T> slow = Head; SNode<T> fast = Head.Next; while (fast != null && fast.Next != null) { slow = slow.Next; fast = fast.Next.Next; if (slow == fast) return true; } return false; }
合并2个有序链表
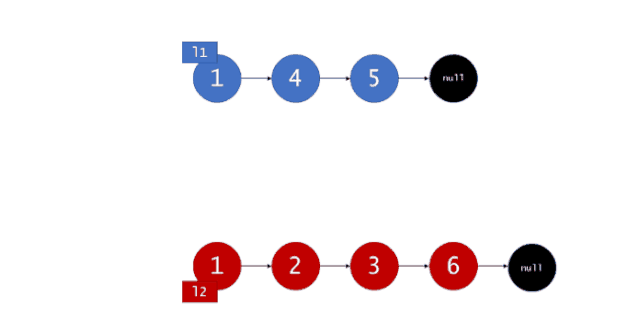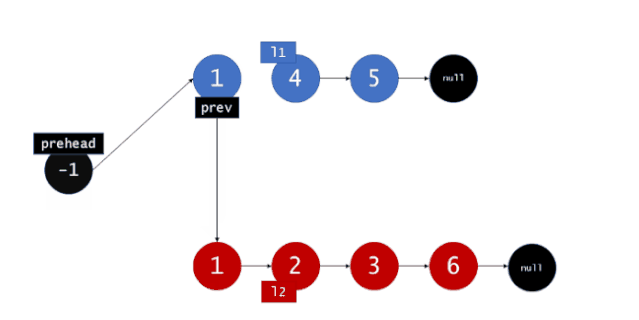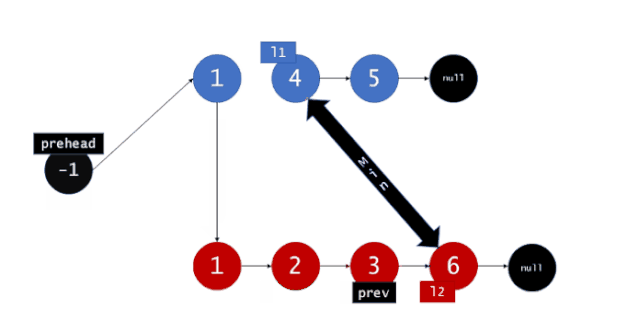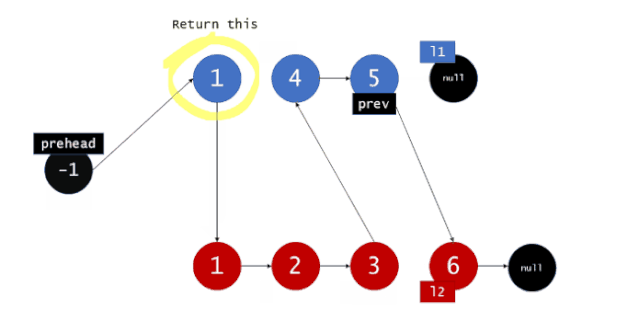
对于2个有序链表,因为链表链表是有序的,因此我们可以依次来取出比较,我们可以用2个指针分别指向2个链表并在链表上进行移动,在比较的过程中依次将取得的结点组成一条新的链表。当有一个指针移动到链表尾时,再将另一条链表剩下的结点连接到新建列表尾即可。如图,
那现在,我们来试着实现一下。
public SNode<int> mergeTwoLists(SNode<int> l1, SNode<int> l2) { SNode<int> soldier = new SNode<int>(0);//利用哨兵节点简化实现难度 SNode<int> p = soldier;//用来存储当前指向的指针 while (l1 != null && l2 != null) { if (l1.Value < l2.Value) { p.Next = l1; l1 = l1.Next; } else { p.Next = l2; l2 = l2.Next; } p = p.Next; } if (l1 != null) p.Next = l1; if (l2 != null) p.Next = l2; return soldier.Next;//新链表的头节点 }
查找链表的中间结点
我们知道,当链表有奇数个结点时,中间结点为一个结点,当链表有偶数个结点时,我们以返回前一个结点来分析。这里,还是用到快慢指针的思想,我们分别将快慢指针slow和fast指向链表的头结点,然后slow每次移动一个结点,fast每次移动2个结点,那么,当fast结点到达链表尾的时候,slow结点即为我们要求的中间结点。我们来分析下,当链表为奇数项时,最后一次fast指针指向链表尾结点,此时,slow指向中间结点;当链表为偶数项时,最后一次,fast.next指针指向链表尾结点,同样的,此时slow刚好指向链表中间位置的前一项。
代码如下:
public SNode<T> findMiddleNode(SNode<T> list) { if (list == null) return null; SNode<T> fast = list; SNode<T> slow = list; while (fast.Next != null && fast.Next.Next != null) { fast = fast.Next.Next; slow = slow.Next; } return slow; }
若是,要返回后一项作为中间结点,那我们得分情况来返回响应值,如下:
public ListNode findMiddleNode(ListNode head) { if (head == null) return head; ListNode fast = head; ListNode slow = head; while (fast.next != null && fast.next.next != null) { fast = fast.next.next; slow = slow.next; } if (fast.next == null)//奇数 { return slow; } else//偶数项:fast.next.next==null { return slow.next; } }
删除链表倒数第k个结点
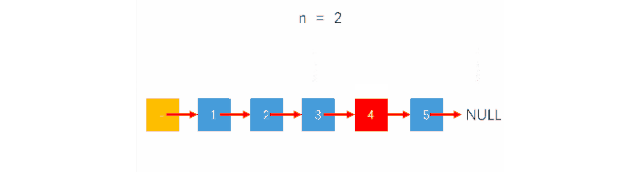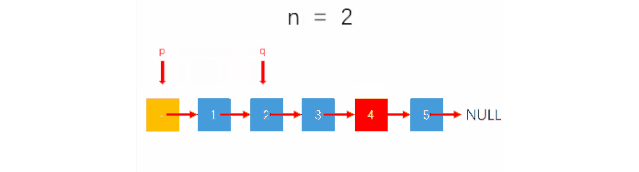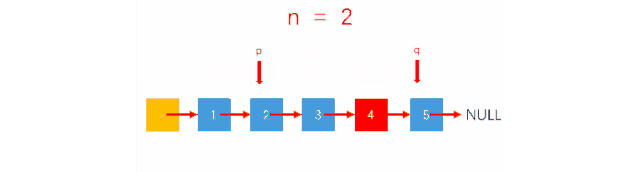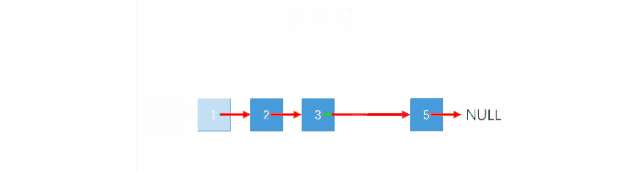
对于单链表,我们并不能从后向前查找结点,那如何才能找到倒数第k个结点的位置呢?还记得我们分析前几个问题时的快慢指针吗?如果我们用2个指针分别指向链表的头结点,然后让其中的一个指针先移动k步,每次移动一个结点,然后,从此时开始,2个结点同时移动,都是每次移动一步,那么,当先移动的指针到达链表尾时,后移动的指针是不是刚好指向倒数第k个位置呢?没错,这个问题的求解思想就是这样的。如图:
(动图这里是先让快指针移动k+1步,然后再2个指针同时移动,但终止条件是fast==null,和先移动k步,然后判断fast.next==null是一样的道理。)那么,我们来看一下具体的代码实现
public SNode<T> deleteLastKth(SNode<T> list, int k) { SNode<T> fast = list; SNode<T> slow = list; int i = 1; while (fast != null && i < k) { fast = fast.Next; i++; } if (fast.Next == null) { list = list.Next; } while (fast.Next != null) { fast = fast.Next; slow = slow.Next; } slow.Next = slow.Next.Next; return list; }
至此,我们的5个问题就讲解完成了,其实,除了我上述讲解的思路,很多问题是可以通过递归的思想来处理的,比如说上述的链表反转、合并2个有序链表问题,如果,你对递归比较了解,可以试着分析一下这两个问题的递归实现。
其实,链表的算法,考察的主要是思维模式而不是代码实现,不管何种算法,其实主要的是要掌握其分析思想,另外,想要写出Bug free的代码,就是要多写多练。俗话说,书读千遍其义自见、眼过千遍不如手过一遍都是一样的道理。只有真正的明白了其处理思想才能更轻松的写出其实现,希望大家开动脑筋多多思考,希望这篇文章对你们能有帮助。