
只用99行代码,你也可以像《冰雪奇缘》里的艾莎公主一样拥有冰雪魔法。
虽然你不能在现实世界中肆意变出魔法,但却能在计算机的虚拟世界挥洒特效。
版权声明:本文内容由阿里云实名注册用户自发贡献,版权归原作者所有,阿里云开发者社区不拥有其著作权,亦不承担相应法律责任。具体规则请查看《阿里云开发者社区用户服务协议》和《阿里云开发者社区知识产权保护指引》。如果您发现本社区中有涉嫌抄袭的内容,填写侵权投诉表单进行举报,一经查实,本社区将立刻删除涉嫌侵权内容。
本文转自量子位(ID:QbitAI) 边策 鱼羊 发自 凹非寺 量子位 报道 | 公众号 QbitAI 只用99行代码,你也可以像《冰雪奇缘》里的艾莎公主一样拥有冰雪魔法。
虽然你不能在现实世界中肆意变出魔法,但却能在计算机的虚拟世界挥洒特效。

或许你不知道,电影和动画中特效有时仅仅短短的一秒,却可能需要高性能计算机演算一周,花费惊人。
《冰雪奇缘》没有真人出演,预算却高达1.5亿美元,每一秒的镜头都是经费在燃烧。一般人想用电脑做出CG特效简直不可想象。
然而,最近一位来自中国的MIT博士,开发了一种新的CG特效编程语言Taichi(太极),大大降低了门槛。

△白色:雪;红色:果冻;蓝色:水 一个简单的物理场景,普通PC仅需几分钟即可渲染完成,相比TensorFlow提速了188倍、比PyTorch快13.4倍,代码长度只有其他底层方法的十分之一。
安装它就像TensorFlow一样容易,使用起来也是差不多:
import taichi as ti
甚至,Taichi的发明者胡渊鸣同学还为此编写了完整使用教程。
关于Taichi,胡同学已经发表了多篇文章,分别被SIGGRAGH 2018、ICRA 2019、NeurIPS2019、ICLR 2020等顶会收录。
计算机图形学知名学者、北大教授陈宝权给出很高的评价:
给胡渊鸣同学点赞!一己之力开发了物理模拟编程语言 Taichi!
像渊鸣这样如此投入写有影响力的开源代码实在是难能可贵。
像SIGGRAPH这样的,可能要投入1~2年才会有成果,论文接受率低,即使能发表出来,引用率也不高。

网友们在围观之后也纷纷表示:渊鸣大神太强了。
图形+系统+编译,真是创世的快乐。

正如胡同学本人所说,99行代码很短,背后的技术故事却很长。
故事的开头,要从Material Point Method(物质点法)说起。
MPM是一种在影视特效领域广受青睐的模拟连续介质方法,迪士尼的《冰雪奇缘》就用到了这项技术。

但在早期,MPM的运行速度非常慢,比如《冰雪奇缘》里安娜过雪地的镜头,据说要在集群上跑整整一个星期。
为了提高MPM的运行速度和性能,在大四毕业的那个暑假,胡渊鸣投入了Moving Least Squares MPM(MLS-MPM)的研究。

胡渊鸣的灵感是,用移动最小二乘法统一APIC(The Affine Particle-In-Cell Method)中的仿射梯度场(affine velocity field)和MPM中的变形梯度更新(deformation gradient update)两种离散化。
在宾夕法尼亚大学蒋陈凡夫教授的指导下,胡渊鸣等人完成了移动最小二乘物质点法(MLS-MPM)方法的研究,不仅实现了新的应力散度离散化,使MPM的运行速度快了两倍,还成功模拟了MPM此前并不支持的各种新现象。
比如材料切割:

刚性体的双向耦合:
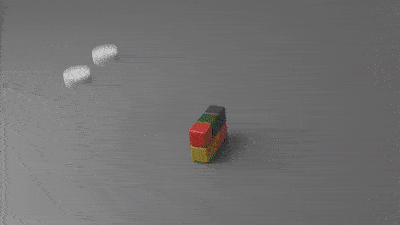
这项成果最终发表在了SIGGRAPH 2018上。
为了进一步证明MLS-MPM的简易性,胡渊鸣用88行C++代码实现了MLS-MPM的demo。(代码详情请戳文末 taichi_mpm 项目链接)。
这个88行版本后来也成为了入门MPM的必备参考实现。

2017年的夏天结束之后,胡渊鸣正式进入MIT读博。
这时候,胡渊鸣又迸发了新的灵感:求出MLS-MPM的导数。有了导数,就能只用梯度下降来优化神经网络控制器。
在这一思想的指导下,ChainQueen诞生了。
胡渊鸣解释说,chain是为了纪念他在求导过程中被链式法则折磨的经历,而ChainQueen则与乾坤谐音。
乾坤基于MLS-MPM,是一种针对可变形对象的、实时的可微混合拉格朗日-欧拉物理模拟器。该模拟器在前向仿真和反向梯度计算中均实现了高精度。

这项研究发表在了ICRA 2019上,胡渊鸣也以此完成了硕士论文。
随后,胡同学将工作又推进一步,提出了可微分编程DiffTaichi,被ICLR 2020收录。
在这篇文章的代码中,胡同学创建了10个不同的物理模拟器,并根据现有基准对其性能进行基准测试。
Taichi中的可微分编程,可以通过蛮力的梯度下降有效地优化神经网络控制器,而不必使用强化学习。
10种可微分模拟器中的大多数模型可以在2-3小时内实现,而且大部分不需要GPU。这些示例中,弹性体、刚体、流体、光线的折射、弹性碰撞,常见物理环境应有尽有。
第一个示例可微分弹性对象模拟器,经过我们的实测,在2017版13寸的MacBook Pro上也能运行,而且完成优化只需不到十分钟的时间:

不仅是2D,更复杂的3D弹性体也能模拟:

还有可微分的3D流体模拟器,经过450步的梯度下降迭代,已经非常逼真:

DiffTaichi模拟水对光线折射的渲染器,一张图片经过它的渲染,甚至能骗过图像分类器。经过测试,VGG16将带有水波纹的松鼠图片当做金鱼,而且认为概率为99.91%。

在强化学习的模拟环境中,刚体机器人很常见,DiffTaichi也能模拟:
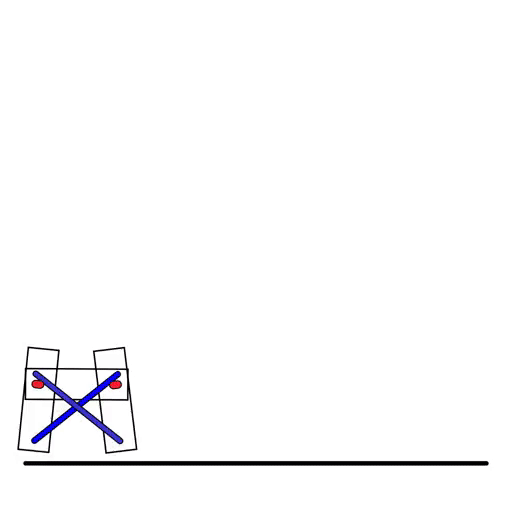
DiffTaichi还能模拟多个物体的复杂场景,比如台球:
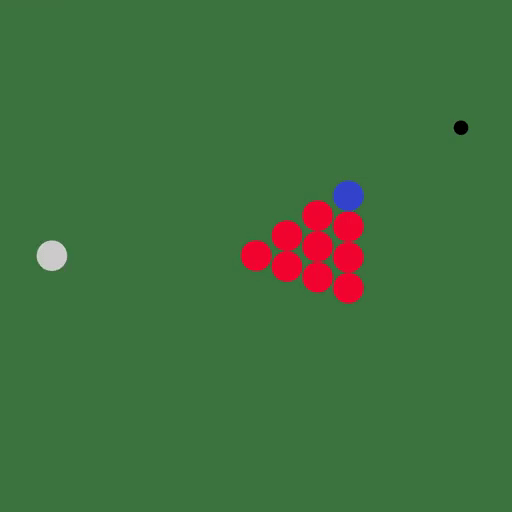
用Taichi语言编写的模拟器大大简化了代码,可微分弹性对象模拟器只用了110行代码,而直接用CUDA编写则需要490行。
同时,Taichi的速度还很快,相比CUDA版本几乎没有什么损失,比TensorFlow快了188倍,比PyTorch快13.4倍。

而且神经网络控制器一般只需要几十次迭代,即可完成优化。
谈到为何要做Taichi,计算机图形学一直缺乏像TensorFlow那样的通用工具,每个要从事开发的人都必须了解基本原理,才能去做编程。
这和深度学习领域形成了鲜明的对比。
近年来,甚至有中学生,利用TensorFlow或者PyTorch,写一点代码,优化几个模型,就可以在一些顶会上发表论文,许多人看来,这是件坏事,因为让深度学习论文的含金量大大降低。
但胡渊鸣看到了另一面。他认为,深度学习这些年之所以能发展快、门槛低,就是因为有简单易用的好工具,计算机图形学让人望而却步,就是因为缺乏类似的工具,因此他开发了Taichi。
本来Taichi要做成一种单独的编程语言,但是为了方便大家使用,胡渊鸣用了一句import taichi as ti把Taichi语言假装成Python。
改成基于Python,这样做的好处不仅是降低学习门槛,还能使用很多现成的Python IDE,与numpy、matplotlib等工具库无缝衔接。
经过几个月的努力,胡渊鸣终于把Taichi改成了pypi安装包,让不同配置不同操作系统的机器都能顺利运行图形学的程序。
说起胡渊鸣,这又是一位从少年时代起就熠熠闪光的“大神级”选手。

高一保送清华,竞赛生涯中,拿下APIO 2012、NOI 2012、ACM-ICPC 2013长沙区域赛、ACM-ICPC上海区域赛四块金牌,其中APIO 2012成绩是全场第一名。
2013年进入清华姚班,胡渊鸣与陈立杰、范浩强等人成为同班同学,这群年轻人的才华在这里汇聚、碰撞,与“姚班”二字相互成就。
本科期间,胡渊鸣先后前往东京大学、斯坦福大学访学,并曾于微软亚洲研究院实习,从事深度学习和计算机图形学研究。本科便有多篇论文中选CVPR、SIGGRAPH等国际顶会。
2017年,胡渊鸣进入MIT读博。入学13个月后,完成硕士论文ChainQueen,拿到MIT硕士学位。博一期间,共发表6篇顶会论文。

代码:
import taichi as ti quality = 1 # Use a larger value for higher-res simulations n_particles, n_grid = 9000 * quality ** 2, 128 * quality dx, inv_dx = 1 / n_grid, float(n_grid) dt = 1e-4 / quality p_vol, p_rho = (dx * 0.5)**2, 1 p_mass = p_vol * p_rho E, nu = 0.1e4, 0.2 # Young's modulus and Poisson's ratio mu_0, lambda_0 = E / (2 * (1 + nu)), E * nu / ((1+nu) * (1 - 2 * nu)) # Lame parameters
x = ti.Vector(2, dt=ti.f32, shape=n_particles) # position v = ti.Vector(2, dt=ti.f32, shape=n_particles) # velocity C = ti.Matrix(2, 2, dt=ti.f32, shape=n_particles) # affine velocity field F = ti.Matrix(2, 2, dt=ti.f32, shape=n_particles) # deformation gradient material = ti.var(dt=ti.i32, shape=n_particles) # material id Jp = ti.var(dt=ti.f32, shape=n_particles) # plastic deformation grid_v = ti.Vector(2, dt=ti.f32, shape=(n_grid, n_grid)) # grid node momemtum/velocity grid_m = ti.var(dt=ti.f32, shape=(n_grid, n_grid)) # grid node mass ti.cfg.arch = ti.cuda # Try to run on GPU
@ti.kernel def substep(): for i, j in ti.ndrange(n_grid, n_grid): grid_v[i, j] = [0, 0] grid_m[i, j] = 0 for p in range(n_particles): # Particle state update and scatter to grid (P2G) base = (x[p] * inv_dx - 0.5).cast(int) fx = x[p] * inv_dx - base.cast(float) # Quadratic kernels [http://mpm.graphics Eqn. 123, with x=fx, fx-1,fx-2] w = [0.5 * ti.sqr(1.5 - fx), 0.75 - ti.sqr(fx - 1), 0.5 * ti.sqr(fx - 0.5)] F[p] = (ti.Matrix.identity(ti.f32, 2) + dt * C[p]) @ F[p] # deformation gradient update h = ti.exp(10 * (1.0 - Jp[p])) # Hardening coefficient: snow gets harder when compressed if material[p] == 1: # jelly, make it softer h = 0.3 mu, la = mu_0 * h, lambda_0 * h if material[p] == 0: # liquid mu = 0.0 U, sig, V = ti.svd(F[p]) J = 1.0 for d in ti.static(range(2)): new_sig = sig[d, d] if material[p] == 2: # Snow new_sig = min(max(sig[d, d], 1 - 2.5e-2), 1 + 4.5e-3) # Plasticity Jp[p] *= sig[d, d] / new_sig sig[d, d] = new_sig J *= new_sig if material[p] == 0: # Reset deformation gradient to avoid numerical instability F[p] = ti.Matrix.identity(ti.f32, 2) * ti.sqrt(J) elif material[p] == 2: F[p] = U @ sig @ V.T() # Reconstruct elastic deformation gradient after plasticity stress = 2 * mu * (F[p] - U @ V.T()) @ F[p].T() + ti.Matrix.identity(ti.f32, 2) * la * J * (J - 1) stress = (-dt * p_vol * 4 * inv_dx * inv_dx) * stress affine = stress + p_mass * C[p] for i, j in ti.static(ti.ndrange(3, 3)): # Loop over 3x3 grid node neighborhood offset = ti.Vector([i, j]) dpos = (offset.cast(float) - fx) * dx weight = w[i][0] * w[j][1] grid_v[base + offset] += weight * (p_mass * v[p] + affine @ dpos) grid_m[base + offset] += weight * p_mass for i, j in ti.ndrange(n_grid, n_grid): if grid_m[i, j] > 0: # No need for epsilon here grid_v[i, j] = (1 / grid_m[i, j]) * grid_v[i, j] # Momentum to velocity grid_v[i, j][1] -= dt * 50 # gravity if i < 3 and grid_v[i, j][0] < 0: grid_v[i, j][0] = 0 # Boundary conditions if i > n_grid - 3 and grid_v[i, j][0] > 0: grid_v[i, j][0] = 0 if j < 3 and grid_v[i, j][1] < 0: grid_v[i, j][1] = 0 if j > n_grid - 3 and grid_v[i, j][1] > 0: grid_v[i, j][1] = 0 for p in range(n_particles): # grid to particle (G2P) base = (x[p] * inv_dx - 0.5).cast(int) fx = x[p] * inv_dx - base.cast(float) w = [0.5 * ti.sqr(1.5 - fx), 0.75 - ti.sqr(fx - 1.0), 0.5 * ti.sqr(fx - 0.5)] new_v = ti.Vector.zero(ti.f32, 2) new_C = ti.Matrix.zero(ti.f32, 2, 2) for i, j in ti.static(ti.ndrange(3, 3)): # loop over 3x3 grid node neighborhood dpos = ti.Vector([i, j]).cast(float) - fx g_v = grid_v[base + ti.Vector([i, j])] weight = w[i][0] * w[j][1] new_v += weight * g_v new_C += 4 * inv_dx * weight * ti.outer_product(g_v, dpos) v[p], C[p] = new_v, new_C x[p] += dt * v[p] # advection
import random group_size = n_particles // 3 for i in range(n_particles): x[i] = [random.random() * 0.2 + 0.3 + 0.10 * (i // group_size), random.random() * 0.2 + 0.05 + 0.32 * (i // group_size)] material[i] = i // group_size # 0: fluid 1: jelly 2: snow v[i] = [0, 0] F[i] = [[1, 0], [0, 1]] Jp[i] = 1
import numpy as np gui = ti.GUI("Taichi MLS-MPM-99", res=512, background_color=0x112F41) for frame in range(20000): for s in range(int(2e-3 // dt)): substep() colors = np.array([0x068587, 0xED553B, 0xEEEEF0], dtype=np.uint32) gui.circles(x.to_numpy(), radius=1.5, color=colors[material.to_numpy()]) gui.show() # Change to gui.show(f'{frame:06d}.png') to write images to disk