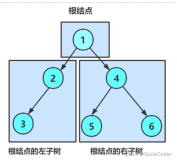
1.二叉树的基本结构及其创建。
#include"stdio.h" #include"stdlib.h" typedef char BTDataType; typedef struct BinaryTreeNode{ struct BinaryTreeNode*left; struct BinaryTreeNode*right; BTDataType data; }BTNode; BTNode *BuyNode(BTDataType x){ BTNode*node=(BTNode*)malloc(sizeof(BTNode)); if(node==NULL){ printf("fail"); exit(-1); } node->data=x; node->left=node->right=NULL; return node; } BTNode*CreatBinaryTree(){ BTNode*nodeA=BuyNode('A'); BTNode*nodeB=BuyNode('B'); BTNode*nodeC=BuyNode('C'); BTNode*nodeD=BuyNode('D'); BTNode*nodeE=BuyNode('E'); BTNode*nodeF=BuyNode('F'); nodeA->left=nodeB; nodeA->right=nodeC; nodeB->left=nodeD; nodeC->left=nodeE; nodeC->right=nodeF; return nodeA; }
2.堆的遍历
所有的遍历有着递归,也就是有着把一个大问题换成很多个小问题
(1)前序遍历(根->左子树->右子树)
先是由根到左子树到右子树 所以先是看A,A不是空后打印A,其实也就相当于打印根,然后左子树,左子树的根B,然后B的左子树根D左树为空,后右树为空,然后是返回B,B的右子树为空,然后返回A进去A的右子树,进入C的根,然后C进入左子树E,E的左右节点为空,然后进入右子树F最后两个空
打印出来后就是ABD NULL NULL C E NULL NULL F NULL NULL
//二叉树前序遍历 void PreOrder(BTNode*root){ if(root==NULL){ printf("NULL"); return; } printf("%c",root->data); PreOrder(root->left); //递归A的左,也就是B再递归B的左,B的左是D也就是说目前是ABD再是NULL空后回到D,再走D的右 PreOrder(root->right); }
(2)中序遍历(左子树->根->右子树)
先是由左子树到根到右子树,进去的是A进A左子树B,进B左子树D,D的左子树是返回NULL然后是返回D,进D的右子树返回NULL,回到B,也返回B,进B右树为NULL,进A 返回A,然后给C的左子树E然后返回左NULL,然后返回C,后再返 NULL,再到F的左子树NULL,再到F最后还是NULL
//二叉树中序遍历 void InOrder(BTNode*root){ if(root==NULL){ printf("NULL"); return; } InOrder(root->left); printf("%c",root->data); InOrder(root->right);}
(3)后序遍历(左子树->右子树->根)
老套路,先进A的左子树B,再进B的左子树D,返回左右俩个为NULL,然后返回D,再返回B的右子树NULL,再返回B,然后进入右子树C,再去到E,E的左右是空,返回两个空,再到C的右节点F,返回两个NULL,再返回F,然后返回C,返回A
//二叉树后序遍历 void PostOrder(BTNode*root){ if(root==NULL){ printf("NULL"); return; } PostOrder(root->left); PostOrder(root->right); printf("%c",root->data); }