基于预测控制的多架小型直升机编队飞行控制

本部分将介绍多架小型无人直升机编队飞行控制，作为 UAV 高级控制的一个示例。自主编队飞行控制系统设计为“领导者--跟随”模型。为了在系统约束下获得良好的控制性能，将“模型预测控制”应用于随动直升机的平动位置控制。在实时最优控制计算中，考虑了运动范围和避碰等位置约束。为了实现对干扰的鲁棒性，使用最小阶干扰观测器来估计不可测量的状态变量和干扰。

编队控制

以鸟类和鱼类为灵感的编队控制是多交通工具系统中的热门话题。在无人机的自主飞行控制中，除了稳定性外，还需要高控制性能。具体可参考机器人编队控制。

在本部分中。首先将直升机动力学建模为线性状态空间方程。其次，利用模型预测控制（MPC）设计了每个跟随器的位置控制器。成本函数以具有终端状态成本的线性二次型形式表示。此外，它还被扩充为一种反映避碰机动和通信范围的形式。

Leader–Follower 系统

此处由于考虑的是直升机，因而 leader 和 follower 之间的追踪可视为一个二维追踪，即 $$\begin{bmatrix} X_{r p} \\ Y_{r p} \end{bmatrix} = \begin{bmatrix} X_{l} + R_{p} \cos \psi_{l} - L_{p} \sin \psi_{l} \\ Y_{l} + R_{p} \sin \psi_{l} + L_{p} \cos \psi_{l}\end{bmatrix}, \quad p = 1, 2, \cdots, n.

$$ - $X_{r p} / Y_{r p}$ 是 follower 在惯性系中的参考轨迹； - $X_{l} / Y_{l}$ 是 leader 在惯性系中的参考轨迹； - $R_{p} / L_{p}$ 是 follower $p$ 相对于 leader 的位置坐标系的偏移量； - $\psi_{l}$ 是 leader 的方向角。 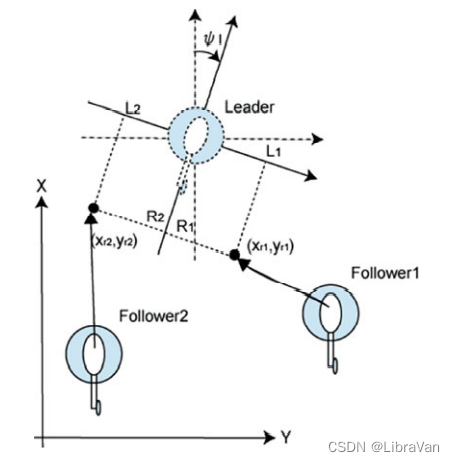 ## 基于模型预测控制的控制器设计 本部分介绍一种分层制导控制器的设计方法，该控制器可使每个跟随者跟踪到指定的参考目标和编队结构。 ### 速度控制模型 首先介绍一个基于修正速度模型 $$\begin{aligned} G_{v x} = - g \frac{b}{s + b} \frac{1}{s - a}, \\ G_{v y} = g \frac{b}{s + b} \frac{1}{s - a}, \end{aligned}$$ 的平移速度和位置模型。 具体而言，现考虑的坐标体系如下图所示。但由于直升机的平动与垂直运动可以独立考虑，在仅考虑平动时，坐标轴取 $X^{\prime}OY^{\prime}$。 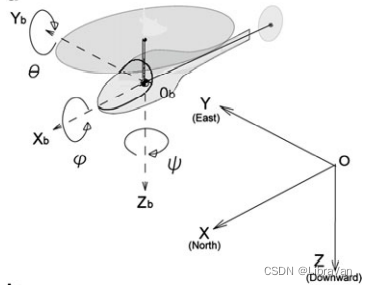 #### 平动模型 假设其平动速率上界为 $5$ m/s，记 ${x}^{\prime}_{v} = [\dot{X}^{\prime} \ \ddot{X}^{\prime} \ \dot{Y}^{\prime} \ \ddot{Y}^{\prime}]^{\rm T}$，$u^{\prime}(t) = [\theta(t) \phi(t)]^{\rm T}$，其平动模型为 $$\begin{aligned} \dot{x}^{\prime}_{v} & = A_{v} x_{x}(t) + B_{v} u^{\prime}(t), \\ y^{\prime}(t) & = C_{v} x^{\prime}_{v}(t). \end{aligned}$$ 其中，$$A_{v} = \begin{bmatrix} 0 & 1 & 0 & 0\\ aT & a - T & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & aT & a - T \end{bmatrix}, \quad B_{v} = \begin{bmatrix} 0 & 0 \\ -gT & 0\\ 0 & 0 \\ 0 & gT \end{bmatrix}, \quad C_{v} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0\end{bmatrix},$$ 且 $T = 2.00$，$a = 0.20$，$g$ 是重力常数。 - 由于速度的测量是在惯性系下进行的，因而需要坐标变换 $$\begin{bmatrix} \dot{X} \\ \dot{Y} \end{bmatrix} = \begin{bmatrix} \cos \psi & - \sin \psi \\ \sin \psi & \cos \psi \end{bmatrix} \begin{bmatrix} \dot{X}^{\prime} \\ \dot{Y}^{\prime} \end{bmatrix},$$ $$\begin{bmatrix} u_{X} \\ u_{Y} \end{bmatrix} = \begin{bmatrix} \cos \psi & - \sin \psi \\ \sin \psi & \cos \psi \end{bmatrix} \begin{bmatrix} \theta \\ \phi \end{bmatrix}.$$ 进而得到系统模型为 $$\begin{aligned} & \dot{x} _{v p \ {\rm argument}} (t) = A_{v} x_{v p}(t) + B_{v} u_{v p} + G_{v} r_{vp}, \\ & A_{v} = \begin{bmatrix} A_{v} & 0_{4 \times 2} \\ -C_{v} & 0_{2 \times 2}\end{bmatrix}, \quad B_{v} = \begin{bmatrix} B_{v} & \\ 0_{2 \times 2}\end{bmatrix}, \quad G_{v} = \begin{bmatrix} 0_{4 \times 2} \\ I_{2 }\end{bmatrix}, \\ & x_{vp \ {\rm argument}} = \begin{bmatrix} x_{v p}^{\rm T}(t) & \varepsilon_{v p}^{\rm T}(t) \end{bmatrix}^{\rm T}. \end{aligned}$$ - 基于上述模型，将性能指标降至最低的反馈控制输入为 $$\begin{aligned} J_{v p} & = \int_{0}^{\infty} x_{v p }^{\rm T}(\tau) Q_{v} x_{v p {\rm argument}}(\tau) + u_{v p}^{\rm T}(\tau) R_{v} u_{v p}(\tau) \; d\tau, \\ Q_{v} & \geq 0, \ R_{v} > 0. \end{aligned}$$ - 进一步地，速度闭环系统为 $$ \dot{x}_{v p \ {\rm argument}} = (A_{v} - B_{v} F_{v}) x_{v p}(t) + G_{v} r_{v p} (t).$$ 则平移位置模型为 $$\begin{aligned} \dot{x}_{p} = A x_{p}(t) + B r_{v p}(t) \\ y_{p} (t) = C x_{p}(t). \end{aligned}$$ 其中，$$A = \begin{bmatrix} 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0_{6 \times 1} & & A_{v}& - & B_{v} & F_{v} & & \end{bmatrix},$$ $$B = \begin{bmatrix} 0_{2 \times 2} \\ G_{v}\end{bmatrix}, \quad C = \begin{bmatrix} I_{2} & 0_{2 \times 6}\end{bmatrix}, \quad x_{p}(t) = \begin{bmatrix} X_{p}(t) & Y_{p}(t) & x_{v p \ {\rm argument}}^{\rm T}\end{bmatrix}^{\rm T}.$$ ### 模型预测控制器设计 利用 MPC (Model Predictive Controller) 方法推导了制导控制器。在 MPC 设计中，以二次形式描述性能指标，并考虑到系统的约束，如碰撞避免和通信范围。 #### 模型预测控制 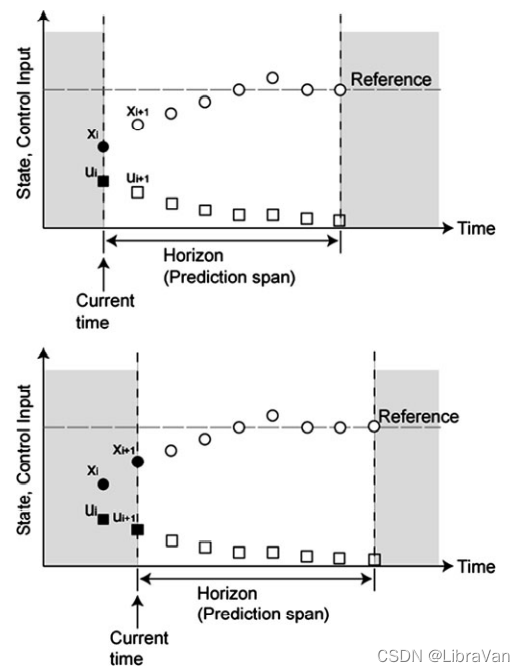 模型预测控制是一种基于模型的控制方法，它在每次考虑系统的轨迹跟踪或约束后，优化从当前时间到未来有限时间的响应。最优控制的范围随着时间的推移而减小，因此，这种方法也被称为后退范围控制。相关可参见[模型预测控制介绍](https://blog.csdn.net/u013414501/article/details/82657583?ops_request_misc=&request_id=&biz_id=102&utm_term=%E6%A8%A1%E5%9E%8B%E9%A2%84%E6%B5%8B%E6%8E%A7%E5%88%B6&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduweb~default-0-82657583.pc_search_result_control_group&spm=1018.2226.3001.4187)。 #### 控制器设计 为了在没有任何跟踪误差的情况下跟踪参考位置设计了伺服系统。扩充状态方程如下 $$\begin{aligned} \dot{x}_{p} & = A x_{p}(t) + B r_{v p}(t) + G r_{p}(t), \\ A & = \begin{bmatrix} A & 0_{8 \times 2} \\ - C & 0_{2 \times 2}\end{bmatrix}, \quad B = \begin{bmatrix} B \\ 0_{2 \times 2}\end{bmatrix}, \quad G = \begin{bmatrix} 0_{8 \times 2} \\ I_{2}\end{bmatrix}, \\ x_{p} & = \begin{bmatrix} x_{p}^{\rm T} & \varepsilon_{p}^{\rm T} \end{bmatrix}^{\rm T}. \end{aligned}$$ 接下来在多架直升机的飞行中设置约束，即通信约束和碰撞约束。 - **通信约束**。当通过改变 $(R_{p}, L_{p})$ 来改变队形时。考虑到每架直升机的通信距离，即 $X_{\min} \leq X_{p} - X_{l} \leq X_{\max}$，$Y_{\min} \leq Y_{p} - Y_{l} \leq Y_{\max}$，设置以下约束条件以限制第 $p$ 个 follower 的位置，$$\begin{aligned} g_{1} (x_{\rm gap}) & = X_{\min} - (X_{p} - X_{l}) \leq 0, \\ g_{2} (x_{\rm gap}) & = (X_{p} - X_{l}) - X_{\max} \leq 0, \\ g_{3} (x_{\rm gap}) & = Y_{\min} - (Y_{p} - Y_{l}) \leq 0, \\ g_{4} (x_{\rm gap}) & = (Y_{p} - Y_{l}) - Y_{\max} \leq 0. \end{aligned}$$ - 进而设置的惩罚函数为 $$P_{j} = \begin{cases} \left[g_{j}x_{p} - \dfrac{\mu_{k}}{2} h_{k}(t)\right]^{2} + 3 \left(\dfrac{\mu_{k} h_{h}(t)}{2}\right)^{2}, \quad g_{j} (x_{a}) > 0, \\ \dfrac{(\mu_{k} h_{k}(t))^{3}}{g_{j}(x_{p}) + \mu_{k} h_{k}(t)}, \quad g_{j} (x_{a}) \leq 0.\end{cases}$$ 此处 $\mu_{k} > \mu_{k + 1} > 0$，$\lim_{k \to \infty} \mu_{k} = 0$，$h_{k}(t) \geq 0$。当 $g_{j} < 0$，$h_{k}(t) = 0$是最优轨迹。 - **碰撞约束**。在第 $p$ 个飞行器处增加人工势函数 $$\begin{aligned} P_{c} & = L \ln \left[a_{p}^{2} (X_{p} - X_{q})^{2} + b_{p}^{2} (Y_{p} - Y_{q})^{2}\right], \\ K & = \begin{cases} K_{o}, \quad & \sqrt{(X_{p} - X_{q})^{2} + (Y_{p} - Y_{q})^{2}} < d, \\ 0, \quad & \sqrt{(X_{p} - X_{q})^{2} + (Y_{p} - Y_{q})^{2}} \geq d. \end{cases}\end{aligned}$$ 此处，$K_{o}$，$a_{p}$，$b_{p}$ 均为调整性能的参数。 在此约束基础上，进而得到最优实时控制。