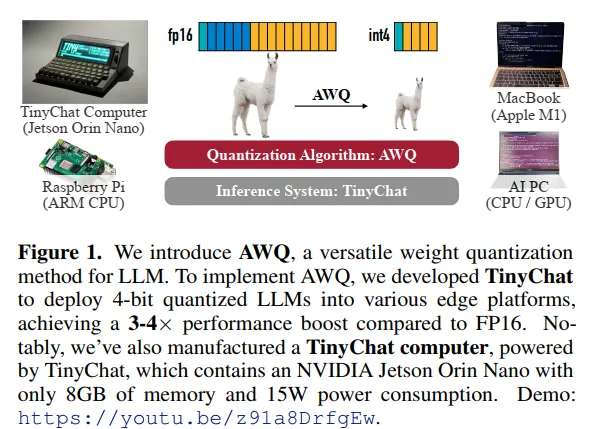
AWQ: 面向设备端大语言模型压缩与加速的激活感知权重量化

Lin J, Tang J, Tang H, et al. Awq: Activation-aware weight quantization for on-device llm compression and acceleration[J]. Proceedings of machine learning and systems, 2024, 6: 87-100.

1. 引言与动机

大语言模型（LLMs）已经在众多人工智能应用中带来了革命性的变革，从GPT-3的1750亿参数到最新的模型规模不断攀升。然而，将这些庞大的模型部署在边缘设备上面临着严峻挑战。以GPT-3为例，其FP16格式需要350GB存储空间，即便是最新的NVIDIA B200 GPU也仅有192GB内存，更不用说资源受限的边缘设备了。设备端部署的重要性体现在多个方面：消除数据传输到云端的延迟，实现离线运行，保护用户隐私，以及大幅降低维护集中式云基础设施的运营成本。

在这种背景下，本文提出了AWQ（Activation-aware Weight Quantization），一种硬件友好的大语言模型低比特权重量化方法。与现有方法不同，AWQ的核心洞察在于权重的重要性应该通过激活分布而非权重本身来判断。这一反直觉的发现引导我们设计了一种简单而有效的按通道缩放策略，既保护了关键权重，又避免了混合精度带来的硬件效率问题。

2. 核心观察与理论基础

2.1 权重重要性的不均等分布

我们的研究始于一个关键观察：大语言模型中的权重并非同等重要。通过系统性实验，我们发现存在一小部分（0.1%-1%）的显著权重，它们对模型性能起着决定性作用。

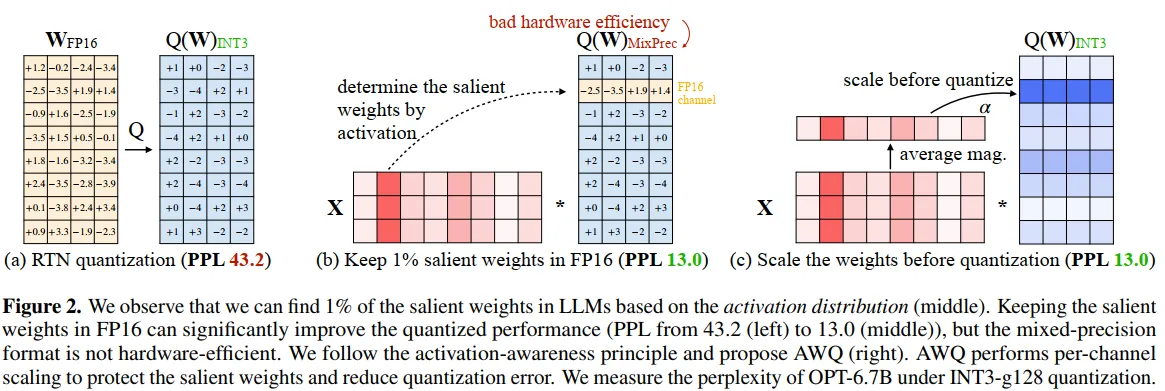
图2详细描述：该图展示了三种不同的量化策略及其对OPT-6.7B模型在INT3-g128量化下的影响。左侧面板展示了简单的RTN（Round-to-Nearest）量化，将FP16权重直接量化到INT3，导致困惑度高达43.2。中间面板展示了保留1%显著权重为FP16精度的混合精度方案，困惑度显著降至13.0，但这种方案需要处理不同精度的数据类型，硬件实现效率低下。右侧面板展示了AWQ的解决方案：通过对显著通道进行缩放（乘以因子$\alpha$），在完全INT3量化的同时达到了与混合精度相当的13.0困惑度。

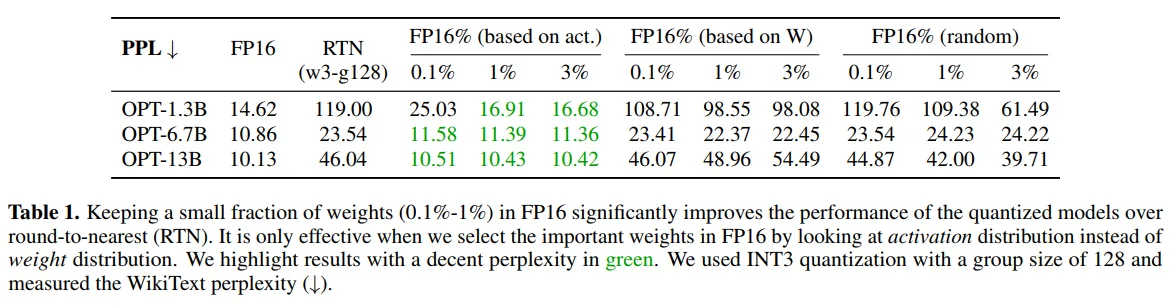
实验数据表明（表1），基于激活分布选择0.1%的权重保持FP16就能将OPT-6.7B的困惑度从23.54降至11.58，而基于权重大小选择的效果（22.37）与随机选择（24.23）相当。这一发现的深层原因在于：具有较大激活幅度的输入特征通常承载着更重要的信息，保护处理这些特征的权重能更好地维持模型的表达能力。

2.2 从激活分布识别显著权重

传统方法通常通过权重的L2范数或绝对值来判断其重要性，但我们的实验表明这种方法在LLM量化中效果不佳。相反，我们提出通过激活分布来识别显著权重通道。具体而言，对于权重矩阵$\mathbf{W} \in \mathbb{R}^{c{out} \times c{in}}$和输入激活$\mathbf{X} \in \mathbb{R}^{c_{in} \times n}$，我们计算每个输入通道的平均激活幅度：

$$s_X^{(i)} = \frac{1}{n} \sum_{j=1}^{n} |X_{ij}|$$

基于$s_X$的值，我们识别出激活幅度最大的前1%通道作为显著通道。这种方法的有效性源于一个基本假设：神经网络倾向于将重要信息编码在幅度较大的激活中。

3. AWQ量化方法

3.1 量化误差的数学分析

为了理解AWQ的工作原理，我们首先分析权重量化带来的误差。考虑一组权重$\mathbf{w}$，线性操作可以写作$\mathbf{y} = \mathbf{w}\mathbf{x}$，量化后的对应操作为$\hat{\mathbf{y}} = Q(\mathbf{w})\mathbf{x}$。

量化函数定义为：
$$Q(w) = \Delta \cdot \text{Round}\left(\frac{w}{\Delta}\right), \quad \text{其中} \quad \Delta = \frac{\max(|\mathbf{w}|)}{2^{N-1}}$$

这里$N$是量化比特数，$\Delta$是量化尺度，由权重组的绝对最大值决定。Round函数将浮点数映射到最近的整数。

现在考虑对权重元素$w \in \mathbf{w}$应用缩放因子$s > 1$，同时对输入$x$进行反向缩放，我们得到：

$$Q(w \cdot s) \cdot \frac{x}{s} = \Delta' \cdot \text{Round}\left(\frac{ws}{\Delta'}\right) \cdot x \cdot \frac{1}{s}$$

其中$\Delta'$是应用缩放后的新量化尺度。

3.2 缩放策略的理论依据

通过大量实验和理论分析，我们发现了三个关键性质：

1. Round误差的稳定性：Round函数的误差在$[-0.5, 0.5]$区间内近似均匀分布，期望值约为0.25，这个性质不受缩放影响。

2. 量化尺度的不变性：当只缩放少数通道时（如1%），通常不会改变整个权重组的最大值，因此$\Delta' \approx \Delta$。

3. FP16精度的无损性：$\Delta$和$x$以FP16表示，在缩放操作中不引入额外量化误差。

基于这些性质，我们可以推导出量化误差的表达式：

$$\text{Err}(Q(w)x) = \Delta \cdot \text{RoundErr}\left(\frac{w}{\Delta}\right) \cdot x$$

$$\text{Err}\left(Q(w \cdot s)\frac{x}{s}\right) = \Delta' \cdot \text{RoundErr}\left(\frac{ws}{\Delta'}\right) \cdot x \cdot \frac{1}{s}$$

误差比率为：
$$\frac{\text{Err}(Q(w \cdot s)(x/s))}{\text{Err}(Q(w)x)} = \frac{\Delta'}{\Delta} \cdot \frac{1}{s}$$

当$\Delta' \approx \Delta$且$s > 1$时，显著权重的相对误差减小了$1/s$倍。

3.3 优化目标与自动搜索

虽然缩放显著权重能减少其量化误差，但过大的缩放因子会增加非显著权重的误差（当$\Delta' > \Delta$时）。因此，我们需要找到最优的缩放策略。

AWQ的优化目标是：
$$\mathbf{s}^* = \arg\min_{\mathbf{s}} L(\mathbf{s})$$

其中损失函数定义为：
$$L(\mathbf{s}) = \|Q(\mathbf{W} \cdot \text{diag}(\mathbf{s}))(\text{diag}(\mathbf{s})^{-1} \cdot \mathbf{X}) - \mathbf{WX}\|_F^2$$

这里$|\cdot|_F$表示Frobenius范数，$\text{diag}(\mathbf{s})$将向量$\mathbf{s}$转换为对角矩阵。

由于量化函数的不可微性，直接优化这个目标函数存在困难。AWQ通过定义一个基于激活的搜索空间来简化问题：

$$\mathbf{s} = \mathbf{s}_X^{\alpha}, \quad \alpha^* = \arg\min_{\alpha \in [0,1]} L(\mathbf{s}_X^{\alpha})$$

这里$\mathbf{s}_X$是每个通道的平均激活幅度，$\alpha$是单一超参数，控制缩放的强度。$\alpha = 0$表示不缩放，$\alpha = 1$表示最激进的缩放。

4. TinyChat推理系统

4.1 性能瓶颈分析

图3详细描述：该图展示了Llama-2-7B在NVIDIA RTX 4090上的性能瓶颈分析。左侧面板显示生成阶段（310ms生成20个token）远慢于上下文阶段（10ms处理200个token）。中间面板展示了roofline分析，横轴是算术强度（FLOPs/Byte），纵轴是峰值TFLOPS。生成阶段在FP16下的算术强度仅为1，远低于GPU的计算内存比165，因此受内存带宽限制。W4A16量化将算术强度提升到4，理论峰值性能从1 TFLOPS提升到4 TFLOPS。右侧面板展示了内存访问分解，权重访问量（134MB）比激活访问量（0.2MB）大近三个数量级，这解释了为什么权重量化对设备端LLM特别有效。

生成阶段的内存瓶颈源于其极低的算术强度。对于批大小为1的推理，每个token生成时需要加载整个模型权重但只处理单个token的激活，导致计算与内存访问的比率极低。

4.2 系统优化技术

TinyChat实现了多层次的优化来充分发挥4比特量化的性能优势：

即时反量化（On-the-fly Dequantization）：传统方法会先将INT4权重反量化为FP16，写入内存，然后进行矩阵运算。TinyChat将反量化操作融合到GEMM内核的主循环中，避免了中间结果的内存访问。对于矩阵乘法$\mathbf{Y} = \mathbf{XW}$，融合后的计算流程为：

for each tile in output:
    load INT4 weights → registers
    dequantize to FP16 in registers
    perform FMA operations
    accumulate to output tile

SIMD感知的权重打包：

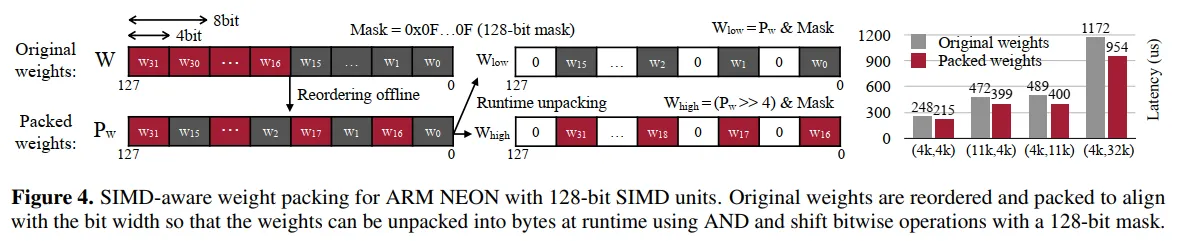
图4详细描述：该图展示了针对128位SIMD单元的ARM NEON架构的权重打包策略。原始权重按照$w_0, w1, ..., w{31}$顺序存储，每个4比特。重新排序后，权重按$w0, w{16}, w1, w{17}, ..., w{15}, w{31}$的模式打包。运行时通过AND操作和位移操作配合128位掩码（0x0F...0F）来解包。这种排列使得32个权重只需3条SIMD指令（一次AND获取低4位，一次右移4位后AND获取高4位）即可全部解包，相比传统方法每个权重需要3条标量指令，效率提升10倍以上。

内核融合策略：

• 层归一化：将均值计算、方差计算、标准化和缩放操作融合为单一内核
• 注意力机制：QKV投影融合，位置编码即时计算，KV缓存在注意力内核内更新
• 激活函数：与前后层操作融合，减少内存往返

5. 实验评估

5.1 语言建模任务

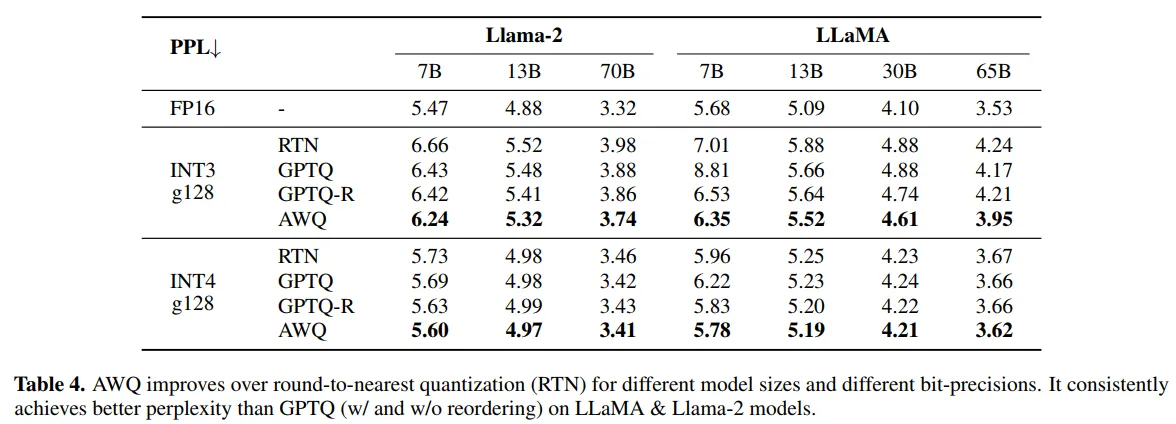
表4展示了AWQ在LLaMA和Llama-2模型族上的全面评估结果。在所有模型规模（7B到70B）和量化设置（INT3/INT4）下，AWQ都达到了最佳性能。特别值得注意的是，AWQ的INT4量化几乎达到了无损压缩——Llama-2-7B的困惑度仅从5.47增加到5.60。

5.2 多模态模型量化

图6和图7的视觉推理示例：
图6展示了LLaVA-13B模型对一个网络meme的理解。图片显示了一盘鸡块，排列方式类似从太空看地球的形状。AWQ正确理解了这个视觉隐喻，描述为"鸡块的排列像从太空看地球"，而RTN错误地描述为"地球和其他行星的小图片放在食物上"。

图7展示了OpenFlamingo-9B在COCO数据集上的字幕生成对比。三组图片分别展示了：(1)两只狗在街上行走，RTN错误识别为"一个人和一只狗"；(2)父女与大象合影，RTN错误描述为"抱着小象"；(3)草地上的玩具飞机，RTN错误识别为"在天空中飞行"。AWQ在所有情况下都给出了准确的描述。

5.3 推理速度评估

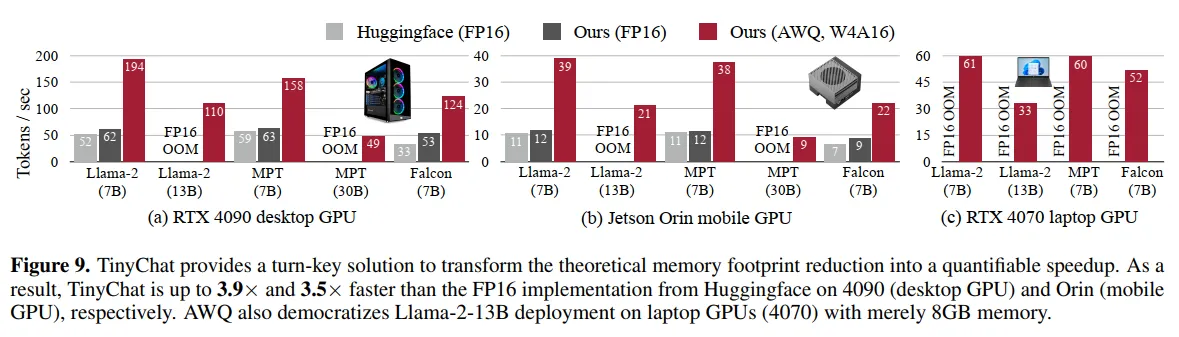
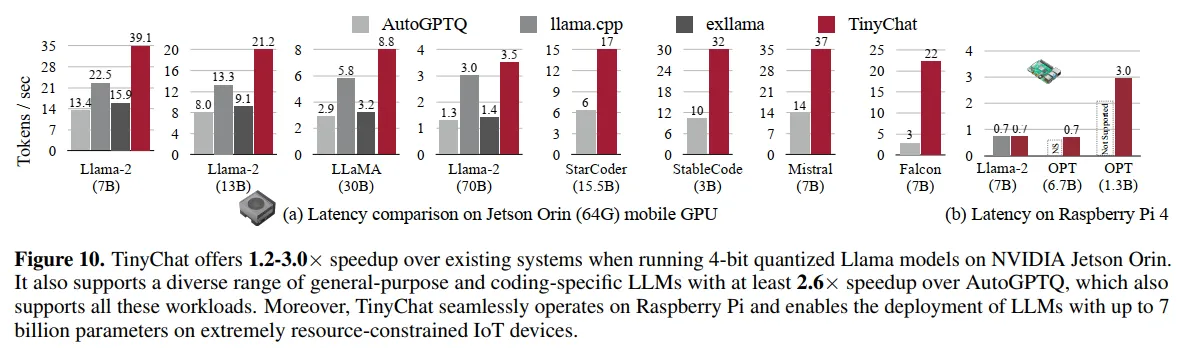
图9和图10的性能对比：
图9展示了TinyChat在不同GPU平台上的速度提升。在RTX 4090上，Llama-2-7B从52 tokens/s提升到194 tokens/s（3.7倍）；在Jetson Orin上达到39 tokens/s；在RTX 4070笔记本GPU上实现33 tokens/s，使得13B模型能在8GB内存上流畅运行。

图10展示了与其他推理系统的对比。在Jetson Orin上，TinyChat达到39.1 tokens/s，而AutoGPTQ为15.9，llama.cpp为22.5，exllama为13.4。更重要的是，TinyChat支持更广泛的模型类型，包括StarCoder（37 tokens/s）、Mistral（32 tokens/s）和Falcon（22 tokens/s）。

5.4 数据效率与泛化能力

图8的详细分析：
左侧面板展示了AWQ的数据效率——仅需16个校准序列（32K tokens）就能达到接近最优的量化性能，而GPTQ需要192个序列才能收敛。右侧面板展示了对校准集分布的鲁棒性实验。使用PubMed数据校准但在Enron邮件上评估时，AWQ的困惑度仅增加0.60，而GPTQ增加4.89。这种鲁棒性使AWQ能够使用通用校准集而不需要针对特定任务进行调整。

6. 深入分析与讨论

6.1 为什么激活感知优于权重感知

传统量化方法基于权重大小来判断重要性，这在卷积神经网络中效果良好，但在Transformer架构的LLM中失效。我们认为这是因为：

1. 信息流的不对称性：在自注意力机制中，信息通过激活而非权重在token之间流动
2. 层归一化的影响：频繁的归一化操作使得权重大小不再直接反映其重要性
3. 残差连接的作用：残差路径使得激活的分布比权重更能反映信息的重要性

6.2 极低比特量化的可能性

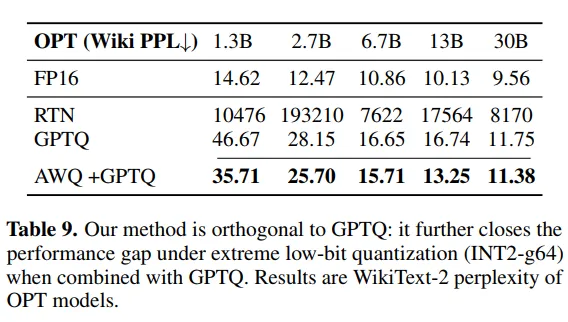
表9展示了AWQ与GPTQ结合进行INT2量化的结果。虽然INT2量化带来了显著的性能下降，但AWQ+GPTQ的组合使其变得可行——OPT-6.7B的困惑度从纯GPTQ的16.65降至15.71。这表明通过更精细的重要性识别和保护策略，2比特量化可能成为实用的选择。

6.3 混合专家模型的量化

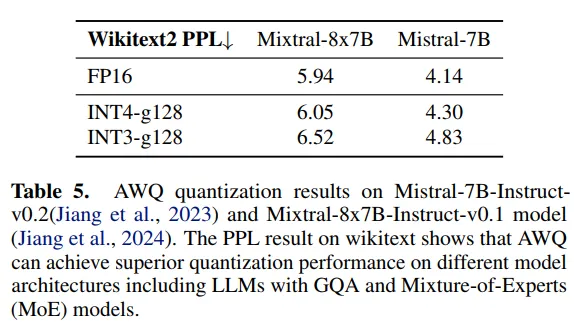
表5展示了AWQ在Mixtral-8x7B这种混合专家（MoE）模型上的效果。MoE架构的稀疏激活特性与AWQ的激活感知策略天然契合，INT4量化仅将困惑度从5.94增加到6.05，展现了AWQ对新型架构的良好适应性。

7. 结论

AWQ通过深刻理解大语言模型中权重重要性的本质，提出了基于激活分布的量化策略。这种方法不仅在理论上优雅，在实践中也展现了卓越的性能。通过TinyChat系统的精心实现，AWQ将4倍的内存节省转化为3倍以上的实际速度提升，真正实现了大语言模型在边缘设备上的实用化部署。

AWQ的成功启发我们：在设计模型压缩方法时，理解模型的内在工作机制比简单地应用通用技术更重要。激活感知的思想不仅适用于量化，也可能为剪枝、知识蒸馏等其他压缩技术提供新的视角。

附录：数学推导

A. 量化误差

考虑权重矩阵$\mathbf{W} \in \mathbb{R}^{m \times n}$和输入$\mathbf{X} \in \mathbb{R}^{n \times b}$，输出为$\mathbf{Y} = \mathbf{WX}$。

对于均匀量化，量化函数定义为：
$$Q(w) = \text{clip}\left(\text{Round}\left(\frac{w}{\Delta}\right), -2^{N-1}, 2^{N-1}-1\right) \cdot \Delta$$

其中clip函数确保量化后的值在表示范围内。

量化误差可以分解为：
$$\mathbf{E} = Q(\mathbf{W})\mathbf{X} - \mathbf{WX} = (Q(\mathbf{W}) - \mathbf{W})\mathbf{X} = \mathbf{E}_W \mathbf{X}$$

其中$\mathbf{E}_W = Q(\mathbf{W}) - \mathbf{W}$是权重量化误差。

对于单个权重$w$，量化误差为：
$$e_w = Q(w) - w = \Delta \cdot \text{Round}\left(\frac{w}{\Delta}\right) - w$$

设$w = k\Delta + r$，其中$k$是整数，$r \in [-\Delta/2, \Delta/2)$是余数，则：
$$e_w = \Delta \cdot \text{Round}\left(k + \frac{r}{\Delta}\right) - k\Delta - r = -r$$

因此量化误差在$[-\Delta/2, \Delta/2]$范围内。

B. 缩放对量化误差的影响

考虑对权重$w$应用缩放因子$s$，新的量化过程变为：

1. 缩放后的权重：$w' = sw$
2. 新的量化尺度：$\Delta' = \max(|\mathbf{w}'|) / (2^{N-1})$
3. 量化：$Q(w') = \Delta' \cdot \text{Round}(w'/\Delta')$
4. 输出：$y' = Q(w') \cdot (x/s)$

误差分析：
$$e' = Q(w') \cdot \frac{x}{s} - wx = \Delta' \cdot \text{Round}\left(\frac{sw}{\Delta'}\right) \cdot \frac{x}{s} - wx$$

当$\Delta' \approx \Delta$时（这在只缩放少数通道时通常成立）：
$$e' \approx \Delta \cdot \text{Round}\left(\frac{sw}{\Delta}\right) \cdot \frac{x}{s} - wx$$

相对误差减小因子为：
$$\frac{|e'|}{|e|} \approx \frac{1}{s}$$

C. 最优缩放因子的推导

考虑包含显著和非显著权重的完整模型，设显著权重集合为$\mathcal{S}$，非显著权重集合为$\mathcal{N}$。

总误差为：
$$L(s) = \sum_{i \in \mathcal{S}} \|Q(s \cdot w_i)(x_i/s) - w_i x_i\|^2 + \sum_{j \in \mathcal{N}} \|Q(w_j)x_j - w_j x_j\|^2$$

对于显著权重，误差随$s$增加而减小（按$1/s$）；但当$s$过大导致$\Delta'$显著增加时，非显著权重的误差会增加。

最优缩放因子需要平衡这两种效应：
$$\frac{\partial L}{\partial s} = -\sum_{i \in \mathcal{S}} \frac{2e_i^2}{s^2} + \sum_{j \in \mathcal{N}} 2e_j \frac{\partial e_j}{\partial s} = 0$$

这解释了为什么实验中$s = 2$附近通常是最优的——它在保护显著权重和避免损害非显著权重之间达到了良好平衡。

D. 激活感知搜索空间的理论依据

设输入激活的协方差矩阵为$\mathbf{C}_X = \mathbb{E}[\mathbf{X}\mathbf{X}^T]$，其特征分解为：
$$\mathbf{C}_X = \mathbf{U}\mathbf{\Lambda}\mathbf{U}^T$$

其中$\mathbf{\Lambda} = \text{diag}(\lambda_1, ..., \lambda_n)$是特征值。

激活的平均幅度$\mathbf{s}_X$可以近似为：
$$s_X^{(i)} \approx \sqrt{\lambda_i}$$

因此，使用$\mathbf{s}_X^{\alpha}$作为缩放因子相当于按照激活方差的$\alpha/2$次幂进行缩放，这在信息论意义上是合理的——方差较大的通道承载更多信息，应该获得更强的保护。这种设计不仅简化了搜索空间（从$n$维降到1维），还确保了缩放策略与数据分布的内在结构一致。