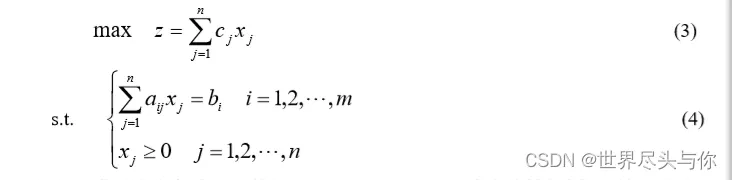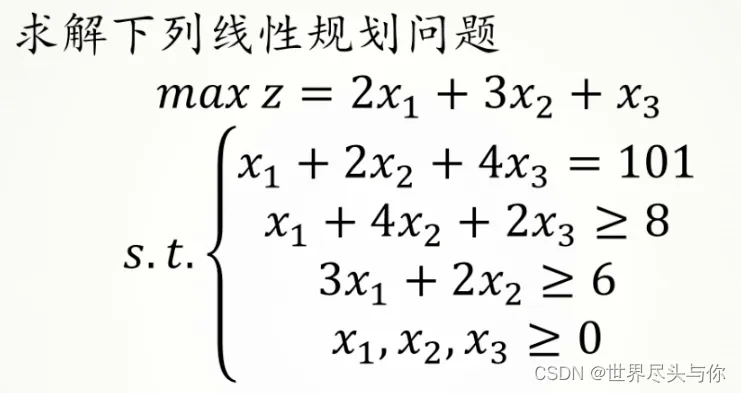1.线性规划
线性规划(Linear programming,简称LP),是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支,是辅助人们进行科学管理的一种数学方法,是研究线性约束条件下线性目标函数的极值问题的数学理论和方法。 线性规划是运筹学的一个重要分支,广泛应用于军事作战、经济分析、经营管理和工程技术等方面。
线性规划问题的目标函数及约束条件均为线性函数;约束条件记为 s.t.(即 subject to)。目标函数可以是求最大值,也可以是求最小值,约束条件的不等号可以 是小于号也可以是大于号。
一般线性规划问题的(数学)标准型为 :
数学建模中常见的线性规划类赛题:
题目中提到“怎样安排/分配”“尽量多(少)”“最多(少)”“利润最大”“最合理”等词
2.Python的解决方案
线性规划求解
案例代码:
''' 线性规划算法 ''' import pulp as pp # 目标函数的系数 z = [2, 3, 1] a = [[1, 4, 2], [3, 2, 0]] b = [8, 6] aeq = [[1, 2, 4]] beq = [101] # 确定最大最小化问题,当前确定的是最大化问题 m = pp.LpProblem(sense=pp.LpMaximize) # 定义三个变量放到列表中 x = [pp.LpVariable(f'x{i}', lowBound=0) for i in [1, 2, 3]] # 定义目标函数,并将目标函数加入求解的问题中 m += pp.lpDot(z, x) # lpDot 用于计算点积 # 设置比较条件 for i in range(len(a)): m += (pp.lpDot(a[i], x) >= b[i]) # 设置相等条件 for i in range(len(aeq)): m += (pp.lpDot(aeq[i], x) == beq[i]) # 求解 m.solve() # 输出结果 print(f'优化结果:{pp.value(m.objective)}') print(f'参数取值:{[pp.value(var) for var in x]}'
程序会输出最终的优化结果:
Welcome to the CBC MILP Solver Version: 2.10.3 Build Date: Dec 15 2019 command line - D:\CodeBox\enpython\lib\site-packages\pulp\apis\..\solverdir\cbc\win\64\cbc.exe D:\ϵͳ��Դ\ϵͳ����\b98f86280e894d38805560900a38bbfe-pulp.mps max timeMode elapsed branch printingOptions all solution D:\ϵͳ��Դ\ϵͳ����\b98f86280e894d38805560900a38bbfe-pulp.sol (default strategy 1) At line 2 NAME MODEL At line 3 ROWS At line 8 COLUMNS At line 20 RHS At line 24 BOUNDS At line 25 ENDATA Problem MODEL has 3 rows, 3 columns and 8 elements Coin0008I MODEL read with 0 errors Option for timeMode changed from cpu to elapsed Presolve 3 (0) rows, 3 (0) columns and 8 (0) elements 0 Obj -0 Primal inf 29.25 (3) Dual inf 5.9999997 (3) 0 Obj -0 Primal inf 29.25 (3) Dual inf 5.1666667e+10 (3) 2 Obj 202 Optimal - objective value 202 Optimal objective 202 - 2 iterations time 0.002 Option for printingOptions changed from normal to all Total time (CPU seconds): 0.01 (Wallclock seconds): 0.01 优化结果:202.0 参数取值:[101.0, 0.0, 0.0]
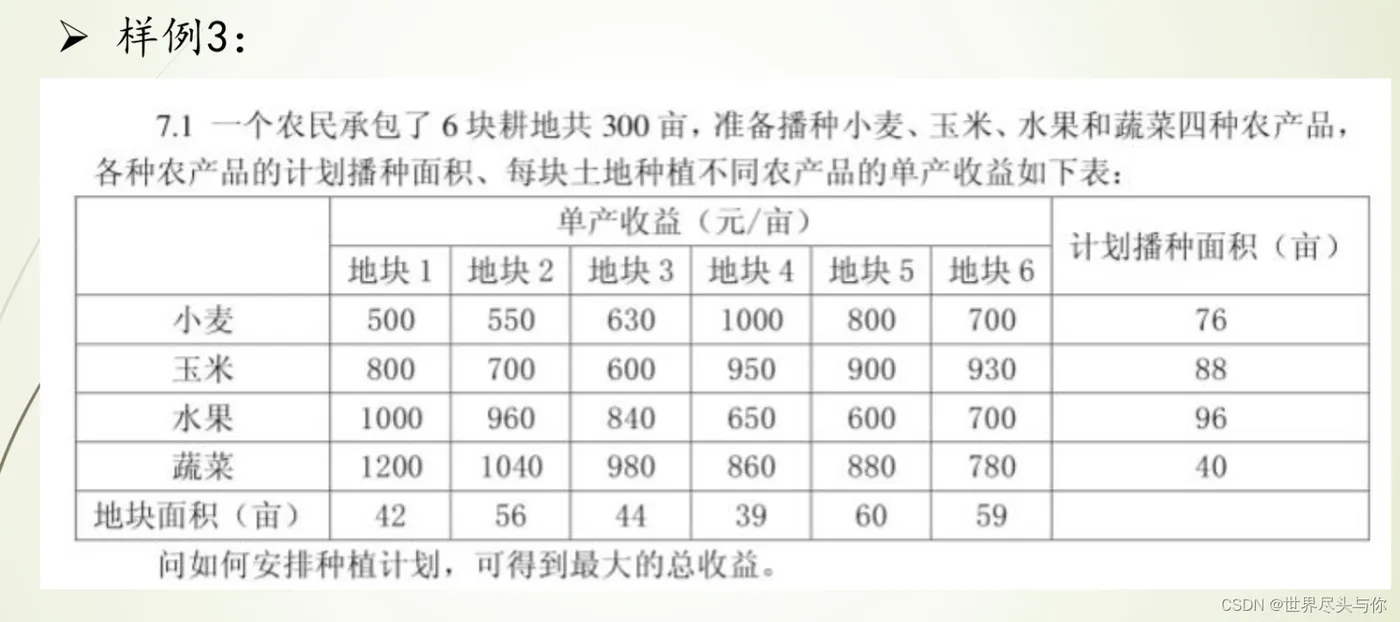
种菜问题
案例代码:
''' 线性规划算法,种菜问题 ''' import pulp import numpy as np from pprint import pprint def transportation_problem(costs, x_max, y_max): row = len(costs) col = len(costs[0]) prob = pulp.LpProblem('Transportation Proble', sense=pulp.LpMaximize) var = [[pulp.LpVariable(f'x{i}{j}', lowBound=0, cat=pulp.LpInteger) for j in range(col)] for i in range(row)] # 转为一维 flatten = lambda x: [y for l in x for y in flatten(l)] if type(x) is list else [x] prob += pulp.lpDot(flatten(var), costs.flatten()) for i in range(row): prob += (pulp.lpSum(var[i]) <= x_max[i]) for j in range(col): prob += (pulp.lpSum([var[i][j] for i in range(row)]) <= y_max[j]) prob.solve() return {'objective': pulp.value(prob.objective), 'var': [[pulp.value(var[i][j]) for j in range(col)] for i in range(row)]} costs = np.array([[500, 550, 630, 1000, 800, 700], [800, 700, 600, 950, 900, 930], [1000, 960, 840, 650, 600, 700], [1200, 1040, 980, 860, 880, 780]]) max_plant = [76, 88, 96, 40] max_cultivation = [42, 56, 44, 39, 60, 59] res = transportation_problem(costs, max_plant, max_cultivation) print(f'最大值为{res["objective"]}') print("各个变量的取值为:") pprint(res['var'])
结果数据:
最大值为284230.0 各个变量的取值为: [[0.0, 0.0, 6.0, 39.0, 31.0, 0.0], [0.0, 0.0, 0.0, 0.0, 29.0, 59.0], [2.0, 56.0, 38.0, 0.0, 0.0, 0.0], [40.0, 0.0, 0.0, 0.0, 0.0, 0.0]]