
请问一下阿里云的MindOpt优化器可以处理带非线性约束的分组背包问题吗?
我需要求解一个分组背包问题,就是下述latex中的X-01矩阵。
但是约束条件比较复杂,想请教一下有什么工具可以进行求解?
谢谢!
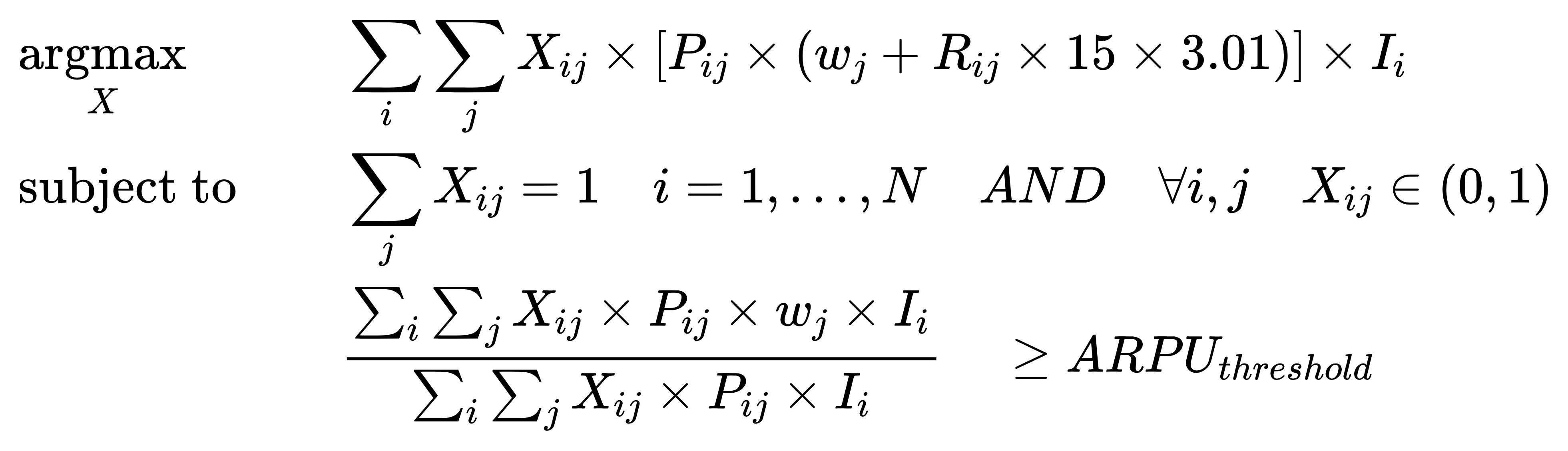
版权声明:本文内容由阿里云实名注册用户自发贡献,版权归原作者所有,阿里云开发者社区不拥有其著作权,亦不承担相应法律责任。具体规则请查看《阿里云开发者社区用户服务协议》和《阿里云开发者社区知识产权保护指引》。如果您发现本社区中有涉嫌抄袭的内容,填写侵权投诉表单进行举报,一经查实,本社区将立刻删除涉嫌侵权内容。
-
云端行者觅知音, 技术前沿我独行。 前言探索无边界, 阿里风光引我情。
分组背包问题是一个经典的组合优化问题,可以用动态规划方法进行求解。如果您想要求解X-01矩阵,可以使用动态规划方法来实现。你也可以将分母乘以ARPU_threshold转换为线性约束来实现。
2023-07-21 15:10:10赞同 展开评论 -
天下风云出我辈,一入江湖岁月催,皇图霸业谈笑中,不胜人生一场醉。
您可以使用不同的优化算法来解决分组背包问题,例如模拟退火算法、遗传算法、粒子群算法等。这些算法可以通过编写相应的代码来实现。此外,您还可以使用商业软件来解决分组背包问题,例如 CPLEX、Mosek、Gurobi 等。这些软件提供了用于解决分组背包问题的内置模块。
需要注意的是,分组背包问题是一个 NP-hard 问题,因此在最坏情况下,解决该问题可能需要大量的时间和内存资源。因此,如果问题规模较大,建议先使用模拟退火算法等启发式算法进行尝试,然后再考虑使用更高级的优化算法或商业软件。2023-07-20 13:58:38赞同 展开评论 -
-
月移花影,暗香浮动
对于复杂的分组背包问题,可以考虑使用数学建模软件和优化求解器来求解。以下是一些常用的工具和软件:
MATLAB:MATLAB是一种强大的数学计算和建模工具,它提供了优化工具箱,可以用于求解各种优化问题,包括分组背包问题。
AMPL:AMPL是一个用于数学建模和优化的语言和环境,它可以帮助你定义复杂的目标函数和约束条件,并使用内置的或外部的优化求解器进行求解。
Gurobi:Gurobi是一种商业优化求解器,提供了高性能的线性规划、整数规划、混合整数规划以及更高级别的优化算法,可以用于求解分组背包问题。
IBM CPLEX:IBM CPLEX是另一种商业优化求解器,它具有处理复杂约束和大规模问题的能力,并提供了用于线性规划、混合整数规划和约束规划的求解方法。
同时提供一段代码仅供参考,以下是使用Python和SciPy库中的linprog函数解决分组背包问题的示例代码:
from scipy.optimize import linprog # 定义问题参数 c = [10, 20, 30] # 每个物品的价值 A = [[-1, -1, -1], [-1, 0, 5], [0, 1, 4]] # 每个物品的重量和价值之间的约束条件 b = [60, 40, 30] # 每个物品的重量限制 x0_bounds = (0, None) # 每个物品的初始重量范围 x1_bounds = (0, None) # 每个物品的最大重量范围 # 调用linprog函数求解问题 res = linprog(c, A_ub=A, b_ub=b, bounds=[x0_bounds, x1_bounds], method='highs') # 输出结果 print('最优解为:', res.x) print('最大价值为:', res.fun)在这个示例中,我们定义了三个物品的价值分别为10、20和30。每个物品的重量和价值之间的约束条件存储在矩阵A中,每个物品的重量限制存储在向量b中。我们还指定了每个物品的初始重量范围和最大重量范围。最后,我们调用linprog函数来求解这个问题,并输出最优解和最大价值。
2023-07-20 09:34:04赞同 展开评论 -
阿里云的MindOpt优化器是一种基于人工智能技术的智能优化平台,可以应用于多个领域的问题。然而,针对具体问题的解答可能需要参考阿里云官方文档或咨询阿里云的技术支持团队来获取更准确的信息。
对于带非线性约束的分组背包问题,通常属于复杂的优化问题。虽然MindOpt优化器在解决一些复杂问题上表现出色,但是否能够处理具体问题需要根据您的问题设置和具体约束条件来评估。
2023-07-19 19:25:18赞同 展开评论 -
面对过去,不要迷离;面对未来,不必彷徨;活在今天,你只要把自己完全展示给别人看。
阿里云的MindOpt优化器可以处理带非线性约束的分组背包问题。MindOpt是一种基于元启发式算法的优化器,它能够应用于多种优化问题,包括带约束的优化问题。
对于带非线性约束的分组背包问题,您可以通过定义适当的目标函数和约束条件来进行建模。然后,将该问题配置到MindOpt中,并使用适当的参数和设置来运行优化过程。
需要注意的是,由于带非线性约束的分组背包问题较为复杂,可能需要更复杂的优化算法和更详细的问题描述来获得较好的结果。您可能需要根据具体情况调整优化器的参数和配置,以达到最佳效果。
2023-07-19 18:57:44赞同 展开评论 -
阿里云的MindOpt优化器是一个全局优化平台,可以用于解决多种复杂的优化问题,包括带非线性约束的分组背包问题。
对于您描述的分组背包问题,您可以使用MindOpt提供的Python SDK来进行建模和求解。您可以通过定义目标函数、约束条件和变量范围来描述问题,并选择适当的求解算法进行求解。
MindOpt支持多种求解算法,包括遗传算法、粒子群算法、模拟退火等,这些算法都可以处理带有非线性约束的优化问题。您可以根据实际情况选择合适的算法进行求解。
另外,MindOpt还提供了丰富的可视化和结果分析功能,可以帮助您更好地理解和优化问题。
2023-07-19 18:38:23赞同 展开评论 -
北京阿里云ACE会长
阿里云的MindOpt优化器可以处理带非线性约束的分组背包问题。分组背包问题(Group Knapsack Problem)是背包问题(Knapsack Problem)的一种扩展,其中物品被分为多个组,每个组中的物品只能选择一个。它是一个NP难问题,需要使用优化工具进行求解。
MindOpt优化器是一种基于云的大规模优化求解器,可以有效地解决各种优化问题,包括约束优化、非线性优化、混合整数规划等。它支持多种约束类型,包括线性约束和非线性约束,可以处理带有非线性约束的分组背包问题。
您可以将分组背包问题转化为一个数学规划问题,并使用MindOpt优化器进行求解。具体来说,您可以使用整数规划或混合整数规划模型来表示分组背包问题,并将非线性约束转化为线性约束或者使用非线性规划模型进行求解。
2023-07-19 18:14:44赞同 展开评论


