逻辑回归模型是一种常用的回归或分类模型,可以视为是广义线性模型的特例。
1.逻辑回归简介
关于线性回归,线性回归是最基本的回归分析方法线性回归研究的是自变量与因变量之间的线性关系。对于传统的线性回归而言,其基本假设是假设y与x直接呈线性关系。如果x与y不是线性关系,则使用线性回归模型会得到较大的误差。
为了解决这个问题,需要寻找一个函数g(y),使g(y)与x之间是线性关系。(即g(y)与y之间不是线性关系,从y到g(y)经历了非线性变换)。这种间接进行对x进行估计的回归,即称为广义线性回归。
2.最大熵模型简介
在信息论中,熵可以度量随机变量的不确定性。当随机变量呈均匀分布时,熵值最大。在一个有序的系统中,有着较小的熵值;而在一个无序的系统中存在着较大的熵值。
在机器学习中,有最大熵原理:描述一个概率分布时,在满足所有约束条件的情况下,熵最大的模型是最好的。
对于离散随机变量x,假设其有M个取值,记$\displaystyle p_i=P(x=i),则其熵定义为:
经过公式推导,最大熵模型与逻辑回归模型之间是完全等价的。
(这里不谈及公式推导的过程。)
3.常用评价指标
3.1混淆矩阵
对二分类问题:
| 真实值 | 预测值0 | 预测值1 |
|---|---|---|
| 0 | True Negative(TN) | False Negative(FP) |
| 1 | False Negative(FN) | True Positive(TP) |
其中,True/False表示判断结果正误,Positive/Negative表示预测值是正标签还是负标签。
| 指标 | 简写 | 描述 |
|---|---|---|
| 真阴率 | TN | 预测成负样本实际是负样本的个数 |
| 假阳率 | FP | 预测成正样本实际是负样本的个数 |
| 假阴率 | FN | 预测成负样本实际是正样本的个数 |
| 真阳率 | TP | 预测成正样本实际是正样本的个数 |
对于多分类问题,则迁移为:
| TN | 预测结果不是该标签,真实标签不是该标签的个数 |
| FP | 预测结果是该标签,真实标签不是该标签的个数 |
| FN | 预测结果不是该标签,真实标签是该标签的个数 |
| TP | 预测结是该标签,真实标签是该标签的个数 |
很多评价指标都是建立在混淆矩阵之上的。
3.2准确率
即预测正确的结果占总样本的百分比,

3.3精确率&召回率
精确率,也称查准率
可以描述为 预测结果是该标签的样例中,实际是该标签的所占比。
召回率,也称查全率

可以描述为 实际是该标签的样例中,预测结果是该标签的所占比。
3.4PR曲线
分类模型对每个样本点都会输出一个置信度。
通过设定置信度的阈值,就可以完成分类。
不同的置信度对应着不同的精确率 和 召回率
一般来说,置信度阈值较低时,大量样本被预测为正例,所以召回率较高,精确率较低;
置信度阈值较高时,大量样本被预测为负例,所以召回率较低,而精确率较高。
PR曲线就是以精确率为纵坐标,以召回率为横坐标做出的曲线。
3.5ROC曲线与AUC
3.5.1ROC曲线
对于二分类分类器,
为了衡量分类器的分类能力,ROC曲线进行了表征:
ROC曲线的横轴为假阳率(False Positive Rate, FPR)

描述: 实际标签为负样本的样本中,预测为正样本的比例。
ROC曲线的纵轴为真阳率(True Positive Rate, TPR)

描述: 实际标签是正样本的样本中,预测为正样本的比例。
通过这两句描述,不看看出,我们更想要的是y轴较大,x轴较小的情况。
- (0, 0)假阳率和真阳率都为0,即分类器全部预测为负样本。
- (0, 1)假阳率为0,真阳率为1,即全部完美预测正确。
- (1, 0)假阳率为1,真阳率为0,即全部完美预测错误。
- (1, 1)假阳率和真阳率都为1,即分类器全部预测为正样本。
ROC曲线的横走坐标都在[0, 1]之间,面积不大于1。
- 当TPR=FPR为一条斜对角线时,表示预测为正样本的结果一般是对的,一般是错的。此为随机分类器的预测效果。
- 当ROC曲线在对角线以下,表示该分类器效果差于随机分类器。
- 当ROC曲线在对角线以上,表示该分类器效果好于随机分类器,我们希望ROC曲线尽可能地位于斜对角线以上,接近左上角(0,1)位置。
3.5.2AUC
AUC(Area Under Curve),即ROC曲线下与坐标轴围成的面积,根据以上表述,可知,
AUC越大,分类器分类效果就越好。
- AUC = 1,表示 是完美分类器,采用这个预测模型时,不管设定什么阈值都能得出完美预测。完美分类器一般不存在。
- 0.5 < AUC < 1,效果好于随机分类器。对于这个分类器,如果设置合适的阈值,则可以有预测价值。
- AUC = 0.5,相当于随机分类器。
- AUC < 0.5,差于随机分类器。(所以可以用于反向预测)
4.基于逻辑回归实现乳腺癌预测
以内置的乳腺癌数据集为例,实现逻辑回归:
from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import recall_score
from sklearn.metrics import precision_score
from sklearn.metrics import classification_report
from sklearn.metrics import accuracy_score
# 获取数据
cancer = load_breast_cancer()
# 分割数据
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, test_size=0.2)
# 创建估计器(实例化逻辑回归模型)
model = LogisticRegression()
# 训练
model.fit(X_train, y_train)
# 返回给定测试数据下的准确率(即预测正确的结果占总样本的百分比)
# 训练集准确率
train_score = model.score(X_train, y_train)
# 测试集准确率
test_score = model.score(X_test, y_test)
print('train score:{train_score:.6f};test score:{test_score:.6f}'.format(train_score=train_score, test_score=test_score))
# 再对X_test进行预测
y_pred = model.predict(X_test)
# 准确率
accuracy_score_value = accuracy_score(y_test, y_pred)
# 精确率
precision_score_value = precision_score(y_test, y_pred)
# 召回率
recall_score_value = recall_score(y_test, y_pred)
# 输出报告模型评估报告
classification_report_value = classification_report(y_test, y_pred)
print("准确率:", accuracy_score_value)
print("精确率:", precision_score_value)
print("召回率:", recall_score_value)
print(classification_report_value)
程序输出结果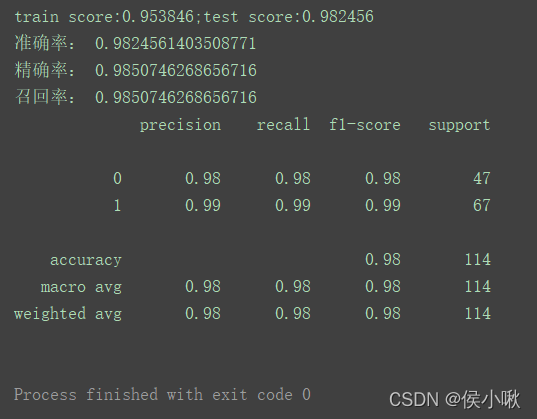
其中,输出准确率,可以使用model对象的score方法,传入参数是特征数据和对应的真实标签。
也可以使用sklearn.metrics的accuracy_score方法,传入参数为真实标签和预测的标签。
参考:
<Python机器学习实战 吕云翔>


