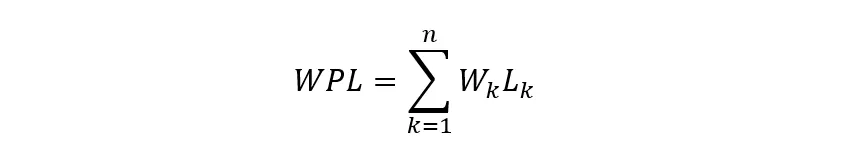求解电文哈弗曼加权路径大小

# include <iostream>
using namespace std ;
typedef struct 
{
 unsigned int weight ; //节点的权值
 unsigned int parent ;
 unsigned int lchild ; 
 unsigned int rchild ;
}HTNode,*HuffmanTree;
//typedef char** HuffmanCode ;
void InitHuffmanTree(HuffmanTree & ,int );
void Select(HuffmanTree HT ,int n,int & s1,int & s2);
int Min_Weight(HuffmanTree HT ,int n );
void InitHuffmanTree(HuffmanTree & HT ,int n);
void HuffmanCoding(HuffmanTree & HT , int n);
int Weight_Length(HuffmanTree HT , int n);// 计算带权路径长度
int Find_length(HuffmanTree HT ,int n);// 计算每个叶子节点到根节点的路径长度
int main(void)
{
 int datanum ; // 数据的组数
 scanf ("%d",&datanum);
 while (datanum)
 {
  HuffmanTree HT;
  int n ;  // 每组数据的个数
  scanf("%d",&n);
  InitHuffmanTree(HT,n); // 初始化哈弗曼树为编码做准备
  HuffmanCoding(HT,n);   // 开始编码
  /*for (int i = 1; i <= 2*n-1 ; i ++) // 此处用于查看内存中的值，检查编码是否正确
  {
   printf ("%5d%5d%5d%5d%5d\n",i,HT[i].weight ,HT[i].lchild ,HT[i].rchild ,HT[i].parent);
  }
  */
  printf("%d\n",Weight_Length(HT,n));
  datanum -- ;
 }
 return 0 ; 
}
int Weight_Length(HuffmanTree HT , int n)
{
 int len = 0 ;
 while (n)
 {
  len = len + Find_length(HT,n) * HT[n].weight ;
  n -- ; 
 }
 return len ; 
}
// 因为从根节点到叶子的路径长度不好找，难以确定走的方向，此处才用的是从叶子到根节点走的方式，每走一步记下，更新长度
int Find_length(HuffmanTree HT ,int n)
{
 int distance = 0 ;
 int f ;
 for (f = HT[n].parent ;f != 0 ; f = HT[f].parent)
 {
  distance ++ ; 
 }
 return distance ;
}
void HuffmanCoding(HuffmanTree & HT , int n)
{
 int m = 2 * n - 1 ;
 for (int i = n + 1 ; i <= m ; i ++)
 {
  int s1,s2;
  Select(HT,i-1,s1,s2); //  在HT中选择两个权值parent为0的相对较小的元素，返回的值中满足s1>=s2的关系
  HT[s1].parent = i ;
  HT[s2].parent = i ;
  HT[i].lchild = s1 ;   
  HT[i].rchild = s2 ;
  HT[i].weight = HT[s1].weight + HT[s2].weight ;
 }
 return ;
}
// 找到两个相对较小的元素并返回
void Select(HuffmanTree HT ,int n,int & s1,int & s2)
{
 s1 = Min_Weight(HT,n);
 s2 = Min_Weight(HT,n);
 return ;
}
int Min_Weight(HuffmanTree HT ,int n )  // 找到相对小的元素并将其标记以表示将其从集合中删去
{
 unsigned int  k = 1000 ; 
 unsigned int min = 0  ;
 int i = 1; 
 while (i <= n )
 {
  if (!HT[i].parent && HT[i].weight < k)
  {
   k = HT[i].weight  ; 
   min = i ;
  }
  i ++ ; 
 }
 HT[min].parent = -1 ;  // 标示找到的较小的元素的位置
 return min;
}

void InitHuffmanTree(HuffmanTree & HT ,int n)
{
 int m = 2*n-1;
 HT = (HuffmanTree)malloc( (m+1) * sizeof(HTNode));  // 此处因为不用0号单元所以得多申请一块内存空间
 if (!HT)
 {
  exit(-1);
 }
 for(int i = 1 ; i <= n ; i ++ )
 {
  scanf("%d",&HT[i].weight);
  HT[i].lchild = 0; 
  HT[i].parent = 0;
  HT[i].rchild = 0;
 }
 for (i = n + 1 ;i <= m ;i ++)
 {
  HT[i].lchild = 0 ;
  HT[i].parent = 0 ; 
  HT[i].rchild = 0 ;
  HT[i].weight = 0 ;
 }
 return ;
}