写在前面:本文主要介绍直接插入排序算法,通过图片一步步解释每一趟每一次的后移。代码通过C#实现,并输出每一次交换的情况和比较次数,方便各位小伙伴比较算法的优缺点。图解堪比Debug,一步步分析每次循环结果。
本文关键字:经典算法、排序算法、插入排序、直接插入排序、图解、C#
一、排序算法分类
- 内部排序
指将需要处理的所有数据都加载到内部存储器(内存)中进行排序。 - 外部排序
数据量过大,无法全部加载到内存中,需要借助外部存储(文件等)进行排序。 - 常见的分类方法

二、算法效率
1. 时间复杂度
度量一个程序(算法)执行时间的两种方法。
- 事后统计的方法
这种方法可行,但有两个问题:一是要想对设计的算法的运行性能进行评测,需要事件运行该程序;二是所得时间的统计量依赖于计算机的硬件、软件等环境因素。 - 事前估算的方法
通过分析某个算法的时间复杂度来判断哪个算法更优。 - 时间频度
一个算法花费的时间与算法中语句的执行次数成正比。一个算法中的语句执行次数称为语句频度或者时间频度。记为T(n)。
此处引用清华大学《数据结构》课程的一段话,一般情况下,算法中的基本操作语句的重复执行次数是问题规模n的某个函数,用T(n)表示,若有某个辅助函数f(n),使得当n趋近于无穷大时,T(n) / f(n) 的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数。记作 T(n)=O( f(n) ),称O( f(n) ) 为算法的渐进时间复杂度,简称时间复杂度。
2. 空间复杂度
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度。有的算法需要占用的临时工作单元数与解决问题的规模n有关,它随着n的增大而增大,当n较大时,将占用较多的存储单元。
三、插入排序
插入式排序属于内部排序法,是对于欲排序的元素以插入的方式找寻该元素的适当位置,以达到排序的目的。
1. 直接插入排序
直接插入排序Insertion Sorting是一种最简单的排序方法,过程就是将每个待排元素逐个插入到已经排好的有序序列中。
2. 拆分插入排序
由于在插入排序的过程中,已经生成了一个(排好的元素组成的)有序数列。所以在插入待排元素时可以使用折半查找的方式更快速的确定新元素的位置,当元素个数较多时,折半插入排序优于直接插入排序。
3. 希尔排序
希尔排序是希尔Donald Shell于1959年提出的一种排序算法。希尔排序也是一种插入排序,它是简单插入排序经过改进之后的一个更高效的版本,也称为缩小增量排序。这里,希尔排序分为交换版本和插入版本,在后续博文我们会具体图解希尔排序和比较这两个版本的区别。感兴趣的小伙伴可以关注一波,谢谢大家。
六、算法实际
1. 图解算法原理
直接插入排序的升序排列基本思想就是把n个待排序的元素看成为一个有序表和一个无序表,开始时有序表中只包含一个元素,无序表中包含有n-1个元素,排序过程中每次从无序表中取出第一个元素,把它的排序码依次与有序表元素的排序码进行比较,将它插入到有序表中的适当位置,使之成为新的有序表。
下面通过一个动图来看一看直接插入排序到底是怎么样移动的。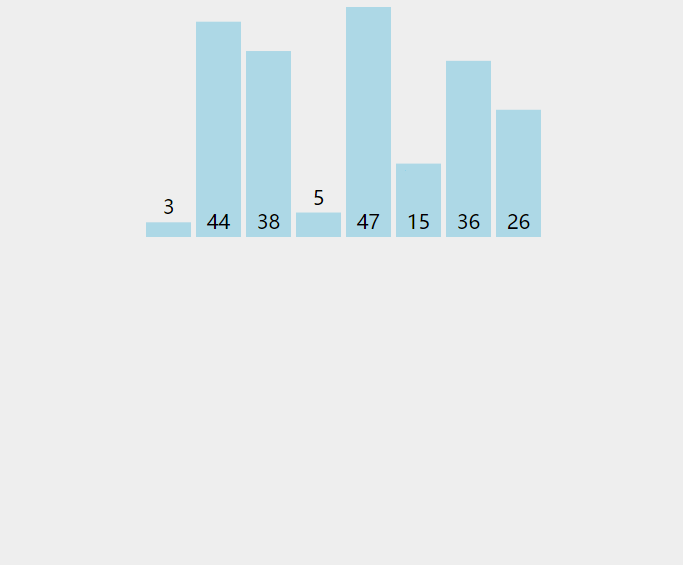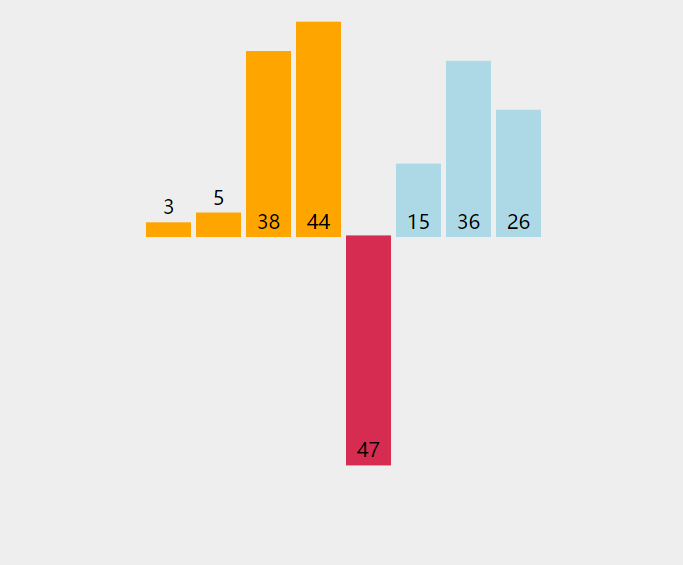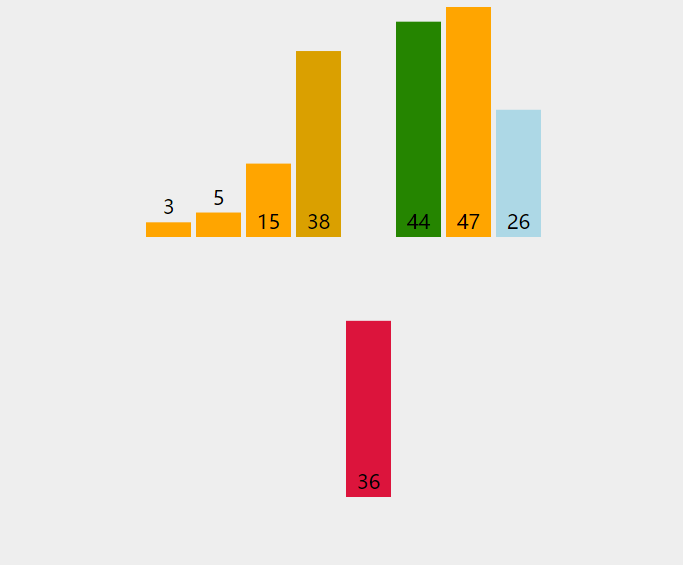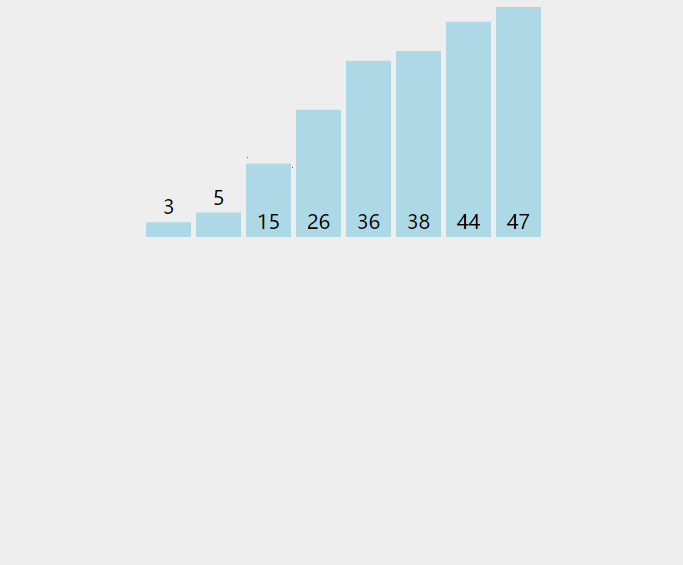
那么,具体是如何移动的,我们以上面动图的数组[3, 44, 38, 5, 47, 15, 36, 26]为例。
假设我们有数组[3, 44, 38, 5, 47, 15, 36, 26],要求按升序排列。
图解约定
- 橙色矩形块表示有序区
- 红色方框表示两数比较
- 红色实线箭头表示插入
- 蓝色箭头表示构造一个临时变量
- 第
i = 0趟
第一个数3,一个数必然有序,所以将3划分有序,后面都是无序。 - 第
i = 1趟

第1趟插入
取第2个数44,首先将44赋值给临时变量insertVal,表示要插入的数。然后比较44的前一个数,也就是3。发现44比3大,此时我们找到了要插入的位置,将insertVal赋值给这个位置。第
i = 2趟
- 第1次后移
取第3个数38,首先将38赋值给临时变量
insertVal,表示要插入的数。然后比较38的前一个数,也就是44。发现38比44小,此时我们将44右移获得如下数组。
- 第2趟插入
紧接着,我们继续比较前一个数也就是3,此时发现38比3大,我们也就找到了38的位置,将
insertVal赋值给这个位置。
第
i = 3趟
- 第1轮后移
取第4个数5,首先将5赋值给临时变量
insertVal,表示要插入的数。然后比较5的前一个数,也就是44。发现5比44小,此时我们将44右移获得如下数组。
- 第2轮后移
同理,5比38小,38往后移动。

- 第3趟插入
紧接着,我们继续比较前一个数也就是3,此时发现5比3大,我们也就找到了5的位置,将
insertVal赋值给这个位置。
第
i = 4趟
- 第4趟插入
取第5个数47,首先将47赋值给临时变量
insertVal,表示要插入的数。然后比较47的前一个数,也就是44。发现47比44大,此时我们找到了要插入的位置,将insertVal赋值给这个位置。第
i = 5趟
- 第1次后移
取第6个数15,首先将15赋值给临时变量
insertVal,表示要插入的数。然后比较15的前一个数,也就是47。发现15比47小,此时我们将47右移获得如下数组。
- 第2和3次后移
同理,38和44分别与15比较并后移,得到以下数组。

- 第5趟次后移
最后,我们比较前一个数也就是5,此时发现15比5大,我们也就找到了15的位置,将
insertVal赋值给这个位置。
后面步骤也很简单,不再给出
2. 算法实现
/// <summary>
/// 直接插入排序静态类
/// </summary>
public static class InsertSort
{
public static void InsertSortMethod(int[] arr)
{
int insertVal = 0;
//使用for循环来把代码简化
for (int i = 1; i < arr.Length; i++)
{
Console.WriteLine($"==============第{i}趟排序==============");
//定义待插入的数
insertVal = arr[i];
int insertIndex = i - 1;
int count = 0;
// 给insertVal 找到插入的位置
// 说明
// 1. j >= 0 保证在给insertVal 找插入位置,不越界
// 2. insertVal < arr[j] 待插入的数,还没有找到插入位置
// 3. 就需要将 arr[j] 后移
for(int j = i - 1; j >= 0 && insertVal < arr[j]; j--)
{
arr[j + 1] = arr[j];
count++;
Console.WriteLine("第" + count + "次后移");
Console.WriteLine(string.Join(" ", arr));
insertIndex = j - 1;
}
// 当退出循环时,说明插入的位置找到, j + 1
//这里我们判断是否需要赋值
if (insertIndex + 1 != i)
{
arr[insertIndex + 1] = insertVal;
}
Console.WriteLine("第"+i+ "趟插入");
Console.WriteLine(string.Join(" ", arr));
}
}
} class Program
{
static void Main(string[] args)
{
//测试直接插入排序
int[] intArray = new int[] { 3, 44, 38, 5, 47, 15, 36, 26 };
InsertSort.InsertSortMethod(intArray);
}
}
==============运行结果===============
==============第1趟排序==============
第1趟插入
3 44 38 5 47 15 36 26
==============第2趟排序==============
第1次后移
3 44 44 5 47 15 36 26
第2趟插入
3 38 44 5 47 15 36 26
==============第3趟排序==============
第1次后移
3 38 44 44 47 15 36 26
第2次后移
3 38 38 44 47 15 36 26
第3趟插入
3 5 38 44 47 15 36 26
==============第4趟排序==============
第4趟插入
3 5 38 44 47 15 36 26
==============第5趟排序==============
第1次后移
3 5 38 44 47 47 36 26
第2次后移
3 5 38 44 44 47 36 26
第3次后移
3 5 38 38 44 47 36 26
第5趟插入
3 5 15 38 44 47 36 26
==============第6趟排序==============
第1次后移
3 5 15 38 44 47 47 26
第2次后移
3 5 15 38 44 44 47 26
第3次后移
3 5 15 38 38 44 47 26
第6趟插入
3 5 15 36 38 44 47 26
==============第7趟排序==============
第1次后移
3 5 15 36 38 44 47 47
第2次后移
3 5 15 36 38 44 44 47
第3次后移
3 5 15 36 38 38 44 47
第4次后移
3 5 15 36 36 38 44 47
第7趟插入
3 5 15 26 36 38 44 47总结
- 这里我们假设数组
[3, 44, 38, 5, 47, 15, 36, 26]为变量arr。- 从以上过程可得,直接插入排序算法是遍历一次所有数,分别插入,但第一个数一定有序,不用排,因此n个数需要n-1次遍历,即i直接从1开始,即
for(int i = 1; i < arr.length; i++)。- 每一次插入的比较都是从前一个数开始,所以我们可以直接将第二个循环的参数j设为i-1,即
for(int j = i - 1; j >= 0; j--),此处j >= 0保证在给insertVal找插入位置,不越界。- 每一次插入我们首先拿出要插入的数,我们将这个数存入临时变量
insertVal中,即insertVal = arr[i]。- 然后比较,如果大于取出数即
insertVal < arr[j],就将这个数后移,即arr[j+ 1] = arr[j]。- 当出现小于取出数
insertVal的数时,跳出循环,因此我们要给第二层循环加一个判断,即for(int j = i - 1; j >= 0 && insertVal > arr[j]; j--)。- 跳出循环后,
insertVal就可以插入数组了,此时下标是j+1,即arr[j + 1] = insertVal。我们通过运行结果可以看出,输出的结果与我们图解分析的内容是一致。
3. 优化版
直接插入排序存在的问题
比如数组 arr = {2,3,4,5,6,1} 这时需要插入的数 1(最小), 这样的过程是:
{2,3,4,5,6,6}
{2,3,4,5,5,6}
{2,3,4,4,5,6}
{2,3,3,4,5,6}
{2,2,3,4,5,6}
{1,2,3,4,5,6}
可以看出当需要插入的数是较小的数时,后移的次数明显增多,对效率有影响。
另一方面:
在插入待排元素时可以使用折半查找的方式更快速的确定新元素的位置,当元素个数较多时,折半插入排序优于直接插入排序。
针对上述问题,我们后续博文会给出解决方案。
4.时间复杂度
若数组是正序的,一趟即可完成排序。最好的时间复杂度为 O(n)。
若数组反序,那么8个数字需要7趟,第1趟比较并后移了1次,第2趟比较2次。最后比较次数是7+6+ ... + 1 = 28次。如果是 n 个数字,那么就是
$$ (n-1)+(n-2)+...+2+1 = n(n-1)/2 = n^2/2 - n/2 $$
根据复杂度的规则,去掉低阶项和常数系数,那复杂度就是 O(n^2)了。
写在结尾:文章中出现的任何错误请大家批评指出,一定及时修改。
希望写在这里的小伙伴能给个三连支持!

