遇到一个叠叠高问题，求解答
A同学买了n张卡片，他想用卡片来叠成一个塔，每层塔由数量不同的房间组成，且高层的房间数量必须少于低层的房间数量，房间可看做两张倾斜的卡片组成，两张卡片上面头部相接触。特殊的，每层的所有房间必须相邻，且高层的房间需要建在天花板上。当 n=13 的时候只有以上两种方法去叠，但只能叠高度为2的塔。相邻两个房间之间用一张卡片作为天花板相连。现在他想知道n张卡片全部使用的情况下他一共可以叠成多少种不同高度的塔。输入一个整数 n(1<=n<=10^9)，表示卡片数量；输出一个数字，可以叠成的高度的种类数。
写回答
-
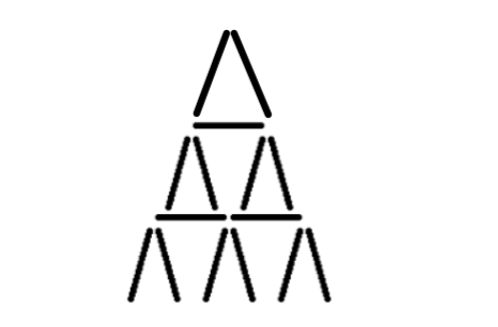
题目中问的是可以组成多少种不同高度的塔。首先计算每种高度的塔至少需要多少张卡片，然后判断多出来的卡片数与至少需要的卡片数之间的关系。观察下图三层的塔。从上向下。第一层一个房间，第二层两个房间，……，第 i 层 i 个房间。一个房间需要 2 张卡片，两个房间需要 5 张卡牌（每个房间 2 张 + 天花板 1张），……，i 个房间需要 2i+i-1=3i-1 张。这样每一层的卡片数都可以计算出来了，前 k 层的卡片数求和即可。记前 k 层最少需要 f(k) 张卡片
接下来观察多余卡片与房间的关系。下图中圈出来的房间位置从1层放到了2层。因此，对于多出来的卡片，我们可以都放到第一层处理（因为题目只问有多少种不同高度，而不是多少种不同的搭建方法）。每多出来一间房，需要 3 张卡片（包括天花板）。所以多余的卡片为 3 的倍数，则这个高度的塔可以搭建。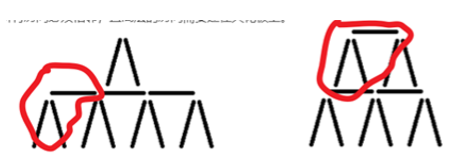
计算过程1. 从第一层开始，计算 f(i)，直到 f(i) 大于 K。 2. 判断每个 f(i) 与 k 的差值是否为 3 的倍数，是，则总数加 1。时间空间复杂度都很小。f(i) 不需要一个数组来保存，只需要算出当前层的直接判断是否为 3 的倍数即可。 因此输入：13 输出：12021-12-23 18:56:48赞同 展开评论 打赏
版权声明：本文内容由阿里云实名注册用户自发贡献，版权归原作者所有，阿里云开发者社区不拥有其著作权，亦不承担相应法律责任。具体规则请查看《阿里云开发者社区用户服务协议》和《阿里云开发者社区知识产权保护指引》。如果您发现本社区中有涉嫌抄袭的内容，填写侵权投诉表单进行举报，一经查实，本社区将立刻删除涉嫌侵权内容。
