
我知道大家会各种花式排序,但是如果叫你打乱一个数组,你是否能做到胸有成竹?即便你拍脑袋想出一个算法,怎么证明你的算法就是正确的呢?乱序算法不像排序算法,结果唯一可以很容易检验,因为「乱」可以有很多种,你怎么能证明你的算法是「真的乱」呢?
所以我们面临两个问题: 1. 什么叫做「真的乱」? 2. 设计怎样的算法来打乱数组才能做到「真的乱」?
这种算法称为「随机乱置算法」或者「洗牌算法」。
本文分两部分,第一部分详解最常用的洗牌算法。因为该算法的细节容易出错,且存在好几种变体,虽有细微差异但都是正确的,所以本文要介绍一种简单的通用思想保证你写出正确的洗牌算法。第二部分讲解使用「蒙特卡罗方法」来检验我们的打乱结果是不是真的乱。蒙特卡罗方法的思想不难,但是实现方式也各有特点的。
一、洗牌算法
此类算法都是靠随机选取元素交换来获取随机性,直接看代码(伪码),该算法有 4 种形式,都是正确的:
// 得到一个在闭区间 [min, max] 内的随机整数
int randInt(int min, int max);
// 第一种写法
void shuffle(int[] arr) {
int n = arr.length();
/******** 区别只有这两行 ********/
for (int i = 0 ; i < n; i++) {
// 从 i 到最后随机选一个元素
int rand = randInt(i, n - 1);
/*************************/
swap(arr[i], arr[rand]);
}
}
// 第二种写法
for (int i = 0 ; i < n - 1; i++)
int rand = randInt(i, n - 1);
// 第三种写法
for (int i = n - 1 ; i >= 0; i--)
int rand = randInt(0, i);
// 第四种写法
for (int i = n - 1 ; i > 0; i--)
int rand = randInt(0, i);
分析洗牌算法正确性的准则:产生的结果必须有 n! 种可能,否则就是错误的。这个很好解释,因为一个长度为 n 的数组的全排列就有 n! 种,也就是说打乱结果总共有 n! 种。算法必须能够反映这个事实,才是正确的。
我们先用这个准则分析一下第一种写法的正确性:
// 假设传入这样一个 arr
int[] arr = {1,3,5,7,9};
void shuffle(int[] arr) {
int n = arr.length(); // 5
for (int i = 0 ; i < n; i++) {
int rand = randInt(i, n - 1);
swap(arr[i], arr[rand]);
}
}
for 循环第一轮迭代时,i=0,rand 的取值范围是 [0,4],有 5 个可能的取值。
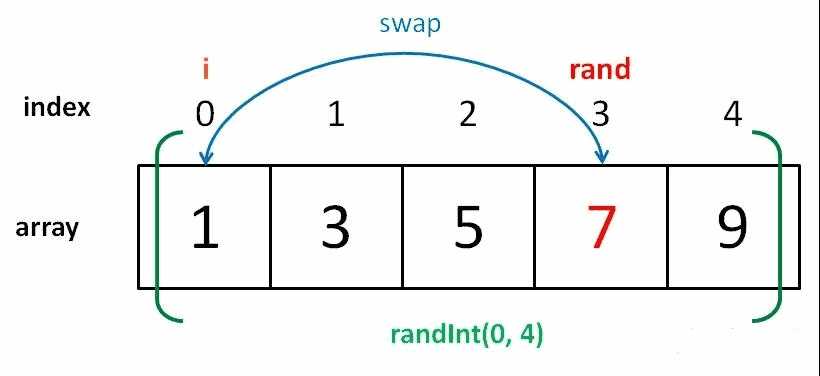
for 循环第二轮迭代时,i=1,rand 的取值范围是 [1,4],有 4 个可能的取值。
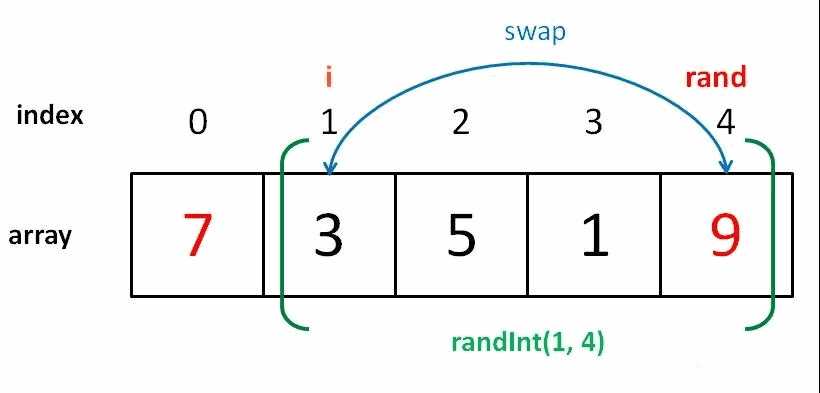
后面以此类推,直到最后一次迭代,i=4,rand 的取值范围是 [4,4],只有 1 个可能的取值。
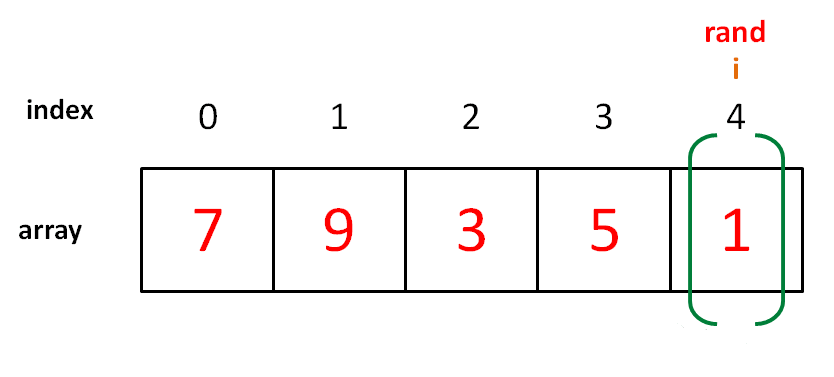
可以看到,整个过程产生的所有可能结果有 54321=5!=n! 种,所以这个算法是正确的。
分析第二种写法,前面的迭代都是一样的,少了一次迭代而已。所以最后一次迭代时 i = 3,rand 的取值范围是 [3,4],有 2 个可能的取值。
// 第二种写法
// arr = {1,3,5,7,9}, n = 5
for (int i = 0 ; i < n - 1; i++)
int rand = randInt(i, n - 1);
所以整个过程产生的所有可能结果仍然有 543*2=5!=n! 种,因为乘以 1 可有可无嘛。所以这种写法也是正确的。
如果以上内容你都能理解,那么你就能发现第三种写法就是第一种写法,只是将数组从后往前迭代而已;第四种写法是第二种写法从后往前来。所以它们都是正确的。
如果读者思考过洗牌算法,可能会想出如下的算法,但是这种写法是错误的:
void shuffle(int[] arr) {
int n = arr.length();
for (int i = 0 ; i < n; i++) {
// 每次都从闭区间 [0, n-1]
// 中随机选取元素进行交换
int rand = randInt(0, n - 1);
swap(arr[i], arr[rand]);
}
}
现在你应该明白这种写法为什么会错误了。因为这种写法得到的所有可能结果有 n^n 种,而不是 n! 种,而且 n^n 一般不可能是 n! 的整数倍。
比如说 arr = {1,2,3},正确的结果应该有 3!=6 种可能,而这种写法总共有 3^3 = 27 种可能结果。因为 27 不能被 6 整除,也就是说总概率不可能被平分,一定有某些情况被「偏袒」了。
后文会讲到,概率均等是算法正确的衡量标准,所以这个算法是错误的。
二、蒙特卡罗方法验证正确性
洗牌算法,或者说随机乱置算法的正确性衡量标准是:对于每种可能的结果出现的概率必须相等,也就是说要足够随机。
如果不用数学严格证明概率相等,可以用蒙特卡罗方法近似地估计出概率是否相等,结果是否足够随机。
记得高中有道数学题:往一个正方形里面随机打点,这个正方形里紧贴着一个圆,告诉你打点的总数和落在圆里的点的数量,让你计算圆周率。

这其实就是利用了蒙特卡罗方法:当打的点足够多的时候,点的数量就可以近似代表图形的面积。通过面积公式,由正方形和圆的面积比值是可以很容易推出圆周率的。当然打的点越多,算出的圆周率越准确,充分体现了大力出奇迹的真理。
类似的,我们可以对同一个数组进行一百万次洗牌,统计各种结果出现的次数,把频率作为概率,可以很容易看出洗牌算法是否正确。整体思想很简单,不过实现起来也有些技巧的,下面简单分析几种实现思路。
第一种思路,我们把数组 arr 的所有排列组合都列举出来,做成一个直方图(假设 arr = {1,2,3}):
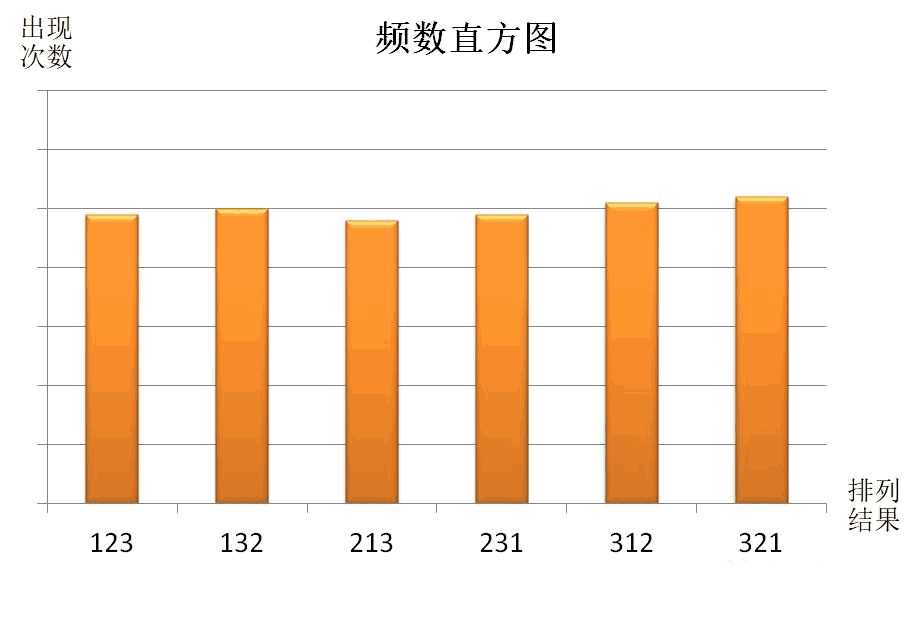
每次进行洗牌算法后,就把得到的打乱结果对应的频数加一,重复进行 100 万次,如果每种结果出现的总次数差不多,那就说明每种结果出现的概率应该是相等的。写一下这个思路的伪代码:
void shuffle(int[] arr);
// 蒙特卡罗
int N = 1000000;
HashMap count; // 作为直方图
for (i = 0; i < N; i++) {
int[] arr = {1,2,3};
shuffle(arr);
// 此时 arr 已被打乱
count[arr] += 1;
}
for (int feq : count.values())
print(feq / N + " "); // 频率
这种检验方案是可行的,不过可能有读者会问,arr 的全部排列有 n! 种(n 为 arr 的长度),如果 n 比较大,那岂不是空间复杂度爆炸了?
是的,不过作为一种验证方法,我们不需要 n 太大,最多用长度为 5 或 6 的 arr 试下就差不多了吧,因为我们只想比较概率验证一下正确性而已。
第二种思路,可以这样想,arr 数组中全都是 0,只有一个 1。我们对 arr 进行 100 万次打乱,记录每个索引位置出现 1 的次数,如果每个索引出现 1 的次数差不多,也可以说明每种打乱结果的概率是相等的。
void shuffle(int[] arr);
// 蒙特卡罗方法
int N = 1000000;
int[] arr = {1,0,0,0,0};
int[] count = new int[arr.length];
for (int i = 0; i < N; i++) {
shuffle(arr); // 打乱 arr
for (int j = 0; j < arr.length; j++)
if (arr[j] == 1) {
count[j]++;
break;
}
}
for (int feq : count)
print(feq / N + " "); // 频率
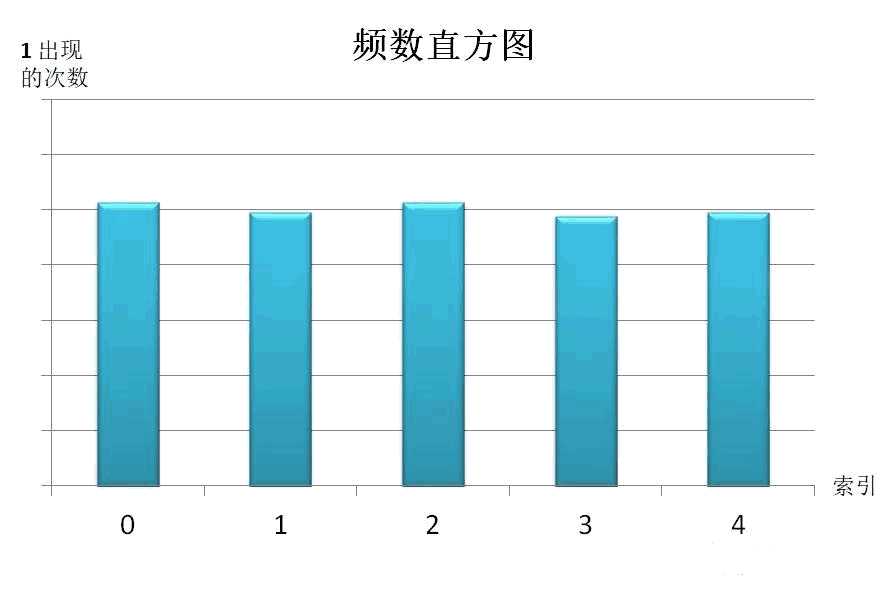
这种思路也是可行的,而且避免了阶乘级的空间复杂度,但是多了嵌套 for 循环,时间复杂度高一点。不过由于我们的测试数据量不会有多大,这些问题都可以忽略。
另外,细心的读者可能发现一个问题,上述两种思路声明 arr 的位置不同,一个在 for 循环里,一个在 for 循环之外。其实效果都是一样的,因为我们的算法总要打乱 arr,所以 arr 的元素顺序并不重要,只要所含元素不变就行。
三、最后总结
本文第一部分介绍了洗牌算法(随机乱置算法),通过一个简单的分析技巧证明了该算法的四种正确形式,并且分析了一种常见的错误写法,相信你一定能够写出正确的洗牌算法了。
第二部分写了洗牌算法正确性的衡量标准,即每种随机结果出现的概率必须相等。如果我们不用严格的数学证明,可以通过蒙特卡罗方法大力出奇迹,粗略验证算法的正确性。蒙特卡罗方法也有不同的思路,不过要求不必太严格,因为我们只是寻求一个简单的验证。
来源 | github
作者 | labuladong
版权声明:本文内容由阿里云实名注册用户自发贡献,版权归原作者所有,阿里云开发者社区不拥有其著作权,亦不承担相应法律责任。具体规则请查看《阿里云开发者社区用户服务协议》和《阿里云开发者社区知识产权保护指引》。如果您发现本社区中有涉嫌抄袭的内容,填写侵权投诉表单进行举报,一经查实,本社区将立刻删除涉嫌侵权内容。