
如题
版权声明:本文内容由阿里云实名注册用户自发贡献,版权归原作者所有,阿里云开发者社区不拥有其著作权,亦不承担相应法律责任。具体规则请查看《阿里云开发者社区用户服务协议》和《阿里云开发者社区知识产权保护指引》。如果您发现本社区中有涉嫌抄袭的内容,填写侵权投诉表单进行举报,一经查实,本社区将立刻删除涉嫌侵权内容。
摘要:面试也是一门学问,在面试之前做好充分的准备则是成功的必须条件,而程序员在代码面试时,常会遇到编写算法的相关问题,比如排序、二叉树遍历等等。
在程序员的职业生涯中,算法亦算是一门基础课程,尤其是在面试的时候,很多公司都会让程序员编写一些算法实例,例如快速排序、二叉树查找等等。
本文总结了程序员在代码面试中最常遇到的10大算法类型,想要真正了解这些算法的原理,还需程序员们花些功夫。
1.String/Array/Matrix
在Java中,String是一个包含char数组和其它字段、方法的类。如果没有IDE自动完成代码,下面这个方法大家应该记住: String/arrays很容易理解,但与它们有关的问题常常需要高级的算法去解决,例如动态编程、递归等。 下面列出一些需要高级算法才能解决的经典问题:
Evaluate Reverse Polish Notation Longest Palindromic Substring 单词分割 字梯 Median of Two Sorted Arrays 正则表达式匹配 合并间隔 插入间隔 Two Sum 3Sum 4Sum 3Sum Closest String to Integer 合并排序数组 Valid Parentheses 实现strStr() Set Matrix Zeroes 搜索插入位置 Longest Consecutive Sequence Valid Palindrome 螺旋矩阵 搜索一个二维矩阵 旋转图像 三角形 Distinct Subsequences Total Maximum Subarray 删除重复的排序数组 删除重复的排序数组2 查找没有重复的最长子串 包含两个独特字符的最长子串 Palindrome Partitioning
2.链表
在Java中实现链表是非常简单的,每个节点都有一个值,然后把它链接到下一个节点。 class Node { int val; Node next;
Node(int x) {
val = x;
next = null;
}
}
比较流行的两个链表例子就是栈和队列。
栈(Stack) class Stack{ Node top;
public Node peek(){
if(top != null){
return top;
}
return null;
}
public Node pop(){
if(top == null){
return null;
}else{
Node temp = new Node(top.val);
top = top.next;
return temp;
}
}
public void push(Node n){
if(n != null){
n.next = top;
top = n;
}
}
}
队列(Queue) class Queue{ Node first, last; public void enqueue(Node n){ if(first == null){ first = n; last = first; }else{ last.next = n; last = n; } } public Node dequeue(){ if(first == null){ return null; }else{ Node temp = new Node(first.val); first = first.next; return temp; }
} }
值得一提的是,Java标准库中已经包含一个叫做Stack的类,链表也可以作为一个队列使用(add()和remove())。(链表实现队列接口)如果你在面试过程中,需要用到栈或队列解决问题时,你可以直接使用它们。
在实际中,需要用到链表的算法有:
插入两个数字 重新排序列表 链表周期 Copy List with Random Pointer 合并两个有序列表 合并多个排序列表 从排序列表中删除重复的 分区列表 LRU缓存
3.树&堆
这里的树通常是指二叉树。 class TreeNode{ int value; TreeNode left; TreeNode right; }
下面是一些与二叉树有关的概念: 二叉树搜索:对于所有节点,顺序是:left children <= current node <= right children; 平衡vs.非平衡:它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树; 满二叉树:除最后一层无任何子节点外,每一层上的所有结点都有两个子结点; 完美二叉树(Perfect Binary Tree):一个满二叉树,所有叶子都在同一个深度或同一级,并且每个父节点都有两个子节点; 完全二叉树:若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
堆(Heap)是一个基于树的数据结构,也可以称为优先队列( PriorityQueue),在队列中,调度程序反复提取队列中第一个作业并运行,因而实际情况中某些时间较短的任务将等待很长时间才能结束,或者某些不短小,但具有重要性的作业,同样应当具有优先权。堆即为解决此类问题设计的一种数据结构。
下面列出一些基于二叉树和堆的算法:
二叉树前序遍历 二叉树中序遍历 二叉树后序遍历 字梯 验证二叉查找树 把二叉树变平放到链表里 二叉树路径和 从前序和后序构建二叉树 把有序数组转换为二叉查找树 把有序列表转为二叉查找树 最小深度二叉树 二叉树最大路径和 平衡二叉树
4.Graph
与Graph相关的问题主要集中在深度优先搜索和宽度优先搜索。深度优先搜索非常简单,你可以从根节点开始循环整个邻居节点。下面是一个非常简单的宽度优先搜索例子,核心是用队列去存储节点。
第一步,定义一个GraphNode class GraphNode{ int val; GraphNode next; GraphNode[] neighbors; boolean visited;
GraphNode(int x) {
val = x;
}
GraphNode(int x, GraphNode[] n){
val = x;
neighbors = n;
}
public String toString(){
return "value: "+ this.val;
}
}
第二步,定义一个队列
class Queue{ GraphNode first, last;
public void enqueue(GraphNode n){
if(first == null){
first = n;
last = first;
}else{
last.next = n;
last = n;
}
}
public GraphNode dequeue(){
if(first == null){
return null;
}else{
GraphNode temp = new GraphNode(first.val, first.neighbors);
first = first.next;
return temp;
}
}
}
第三步,使用队列进行宽度优先搜索 public class GraphTest {
public static void main(String[] args) {
GraphNode n1 = new GraphNode(1);
GraphNode n2 = new GraphNode(2);
GraphNode n3 = new GraphNode(3);
GraphNode n4 = new GraphNode(4);
GraphNode n5 = new GraphNode(5);
n1.neighbors = new GraphNode[]{n2,n3,n5};
n2.neighbors = new GraphNode[]{n1,n4};
n3.neighbors = new GraphNode[]{n1,n4,n5};
n4.neighbors = new GraphNode[]{n2,n3,n5};
n5.neighbors = new GraphNode[]{n1,n3,n4};
breathFirstSearch(n1, 5);
}
public static void breathFirstSearch(GraphNode root, int x){
if(root.val == x)
System.out.println("find in root");
Queue queue = new Queue();
root.visited = true;
queue.enqueue(root);
while(queue.first != null){
GraphNode c = (GraphNode) queue.dequeue();
for(GraphNode n: c.neighbors){
if(!n.visited){
System.out.print(n + " ");
n.visited = true;
if(n.val == x)
System.out.println("Find "+n);
queue.enqueue(n);
}
}
}
}
}
输出结果: value: 2 value: 3 value: 5 Find value: 5 value: 4
实际中,基于Graph需要经常用到的算法:
克隆Graph
15 2014-04-24 18:55:03回复数 293 只看楼主 引用 举报 楼主
柔软的胖纸 Bbs1 5.排序
不同排序算法的时间复杂度,大家可以到wiki上查看它们的基本思想。
BinSort、Radix Sort和CountSort使用了不同的假设,所有,它们不是一般的排序方法。 下面是这些算法的具体实例,另外,你还可以阅读:Java开发者在实际操作中是如何排序的。
归并排序 快速排序 插入排序
6.递归和迭代
下面通过一个例子来说明什么是递归。
问题:
这里有n个台阶,每次能爬1或2节,请问有多少种爬法?
步骤1:查找n和n-1之间的关系
为了获得n,这里有两种方法:一个是从第一节台阶到n-1或者从2到n-2。如果f(n)种爬法刚好是爬到n节,那么f(n)=f(n-1)+f(n-2)。
步骤2:确保开始条件是正确的
f(0) = 0; f(1) = 1; public static int f(int n){ if(n <= 2) return n; int x = f(n-1) + f(n-2); return x; }
递归方法的时间复杂度指数为n,这里会有很多冗余计算。
f(5) f(4) + f(3) f(3) + f(2) + f(2) + f(1) f(2) + f(1) + f(2) + f(2) + f(1)
该递归可以很简单地转换为迭代。
public static int f(int n) {
if (n <= 2){
return n;
}
int first = 1, second = 2;
int third = 0;
for (int i = 3; i <= n; i++) {
third = first + second;
first = second;
second = third;
}
return third;
}
在这个例子中,迭代花费的时间要少些。关于迭代和递归,你可以去 这里看看。
7.动态规划
动态规划主要用来解决如下技术问题:
通过较小的子例来解决一个实例; 对于一个较小的实例,可能需要许多个解决方案; 把较小实例的解决方案存储在一个表中,一旦遇上,就很容易解决; 附加空间用来节省时间。 上面所列的爬台阶问题完全符合这四个属性,因此,可以使用动态规划来解决: public static int[] A = new int[100];
public static int f3(int n) { if (n <= 2) A[n]= n;
if(A[n] > 0)
return A[n];
else
A[n] = f3(n-1) + f3(n-2);//store results so only calculate once!
return A[n];
}
一些基于动态规划的算法: 编辑距离 最长回文子串 单词分割 最大的子数组
8.位操作
位操作符:
从一个给定的数n中找位i(i从0开始,然后向右开始)
public static boolean getBit(int num, int i){ int result = num & (1<<i);
if(result == 0){
return false;
}else{
return true;
}
}
例如,获取10的第二位:
i=1, n=10 1<<1= 10 1010&10=10 10 is not 0, so return true;
典型的位算法: Find Single Number Maximum Binary Gap
9.概率
通常要解决概率相关问题,都需要很好地格式化问题,下面提供一个简单的例子: 有50个人在一个房间,那么有两个人是同一天生日的可能性有多大?(忽略闰年,即一年有365天)
算法:
public static double caculateProbability(int n){ double x = 1;
for(int i=0; i<n; i++){
x *= (365.0-i)/365.0;
}
double pro = Math.round((1-x) * 100);
return pro/100;
}
结果:calculateProbability(50) = 0.97
10.组合和排列
组合和排列的主要差别在于顺序是否重要。
例1:
1、2、3、4、5这5个数字,输出不同的顺序,其中4不可以排在第三位,3和5不能相邻,请问有多少种组合?
例2:
有5个香蕉、4个梨、3个苹果,假设每种水果都是一样的,请问有多少种不同的组合?
基于它们的一些常见算法 排列 排列2 排列顺序 来自: ProgramCreek
转载于:https://bbs.csdn.net/topics/390768965
空间复杂度 算法执行耗费的内存 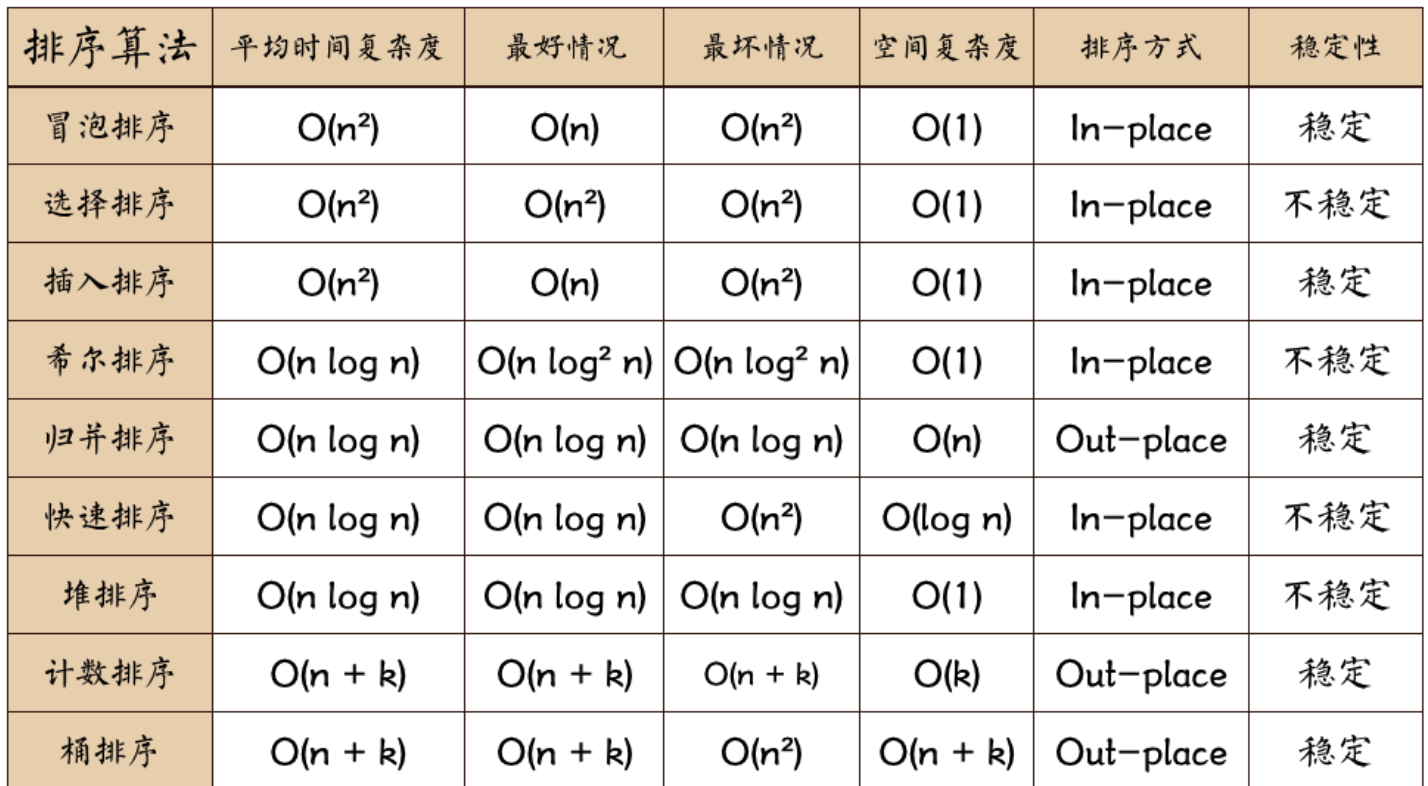 In/out-place: 不占/占额外内存 冒泡排序: 选择排序: 插入排序: 希尔排序: 归并排序: 快速排序: 堆排序: 计数排序: 桶排序: 基数排序:
In/out-place: 不占/占额外内存 冒泡排序: 选择排序: 插入排序: 希尔排序: 归并排序: 快速排序: 堆排序: 计数排序: 桶排序: 基数排序:
提高类 常见算法面试题 Problem 1 : Is it a loop ? (判断链表是否有环?)
Assume that wehave a head pointer to alink-list. Also assumethat we know the list is single-linked. Can you come upan algorithm to checkwhether this link list includes a loop by using O(n) timeand O(1) space wheren is the length of the list? Furthermore, can you do sowith O(n) time and onlyone register?
方法:使用两个指针,从头开始,一个一次前进一个节点,一个前进2个节点,则最多2N,后两个指针可以重合;如果无环,则正常停止。
同样的,可以找到链表的中间节点。同上。
Problem 2:设计一个复杂度为n的算法找到链表倒数第m个元素。最后一个元素假定是倒数第0个。
提示:双指针查找
Problem 3:用最简单的方法判断一个LONG整形的数A是2^n(2的n次方)
提示:x&(x-1)
Problem 4:两个烧杯,一个放糖一个放盐,用勺子舀一勺糖到盐,搅拌均匀,然后舀一勺混合物会放糖的烧杯,问你两个烧杯哪个杂质多?
提示:相同。假设杂质不等,那么将杂质放回原杯中,则杯中物体重量必变化,不合理。
Problem 5:给你a、b两个文件,各存放50亿条url,每条url各占用64字节,内存限制是4G,让你找出a、b文件共同的url。
法1:使用hash表。使用a中元素创建hash表,hash控制在适当规模。在hash中查找b的元素,找不到的url先存在新文件中,下次查找。如果找到,则将相应的hash表项删除,当hash表项少于某个阈值时,将a中新元素重新hash。再次循环。
法2:对于hash表项增加一项记录属于的文件a,b。只要不存在的表项即放入hash表中,一致的项则删除。注意:可能存在很多重复项,引起插入,删除频繁。
Problem 6:给你一个单词a,如果通过交换单词中字母的顺序可以得到另外的单词b,那么定义b是a的兄弟单词。现在给你一个字典,用户输入一个单词,让你根据字典找出这个单词有多少个兄弟单词。
提示:将每个的单词按照字母排序,则兄弟单词拥有一致的字母排序(作为单词签名)。使用单词签名来查找兄弟单词。
Problem 7:五桶球,一桶不正常,不知道球的重量和轻重关系,用天平称一次找出那桶不正常的球。
Problem 8:给两个烧杯,容积分别是m和n升(m!=n),还有用不完的水,用这两个烧杯能量出什么容积的水?
m, n, m+n, m-n以及线性叠加的组合
Problem 9:写出一个算法,对给定的n个数的序列,返回序列中的最大和最小的数。
Problem 10:你能设计出一个算法,只需要执行1.5n次比较就能找到序列中最大和最小的数吗?能否再少?
提示:先通过两两比较,区分大小放入“大”,“小”两个数组中。从而最大数在“大”数组中,最小数在“小”数组中。
Problem 11:给你一个由n-1个整数组成的未排序的序列,其元素都是1到n中的不同的整数。请写出一个寻找序列中缺失整数的线性-时间算法。
提示:累加求和
Problem 12:void strton(constchar* src, const char*token) 假设src是一长串字符,token存有若干分隔符,只要src的字符是token中的任何一个,就进行分割,最终将src按照token分割成若干单词。找出一种O(n)算法?
提示:查表的方法,将所有的字符串存储在长度为128的数组中,并将作为分隔符的字符位置1,这样即可用常数时间判断字符是否为分隔符,通过n次扫描,将src分割成单词。
Problem 13:一个排好序的数组A,长度为n,现在将数组A从位置m(m<n,m未知)分开,并将两部分互换位置,假设新数组记为B,找到时间复杂度为O(lgn)的算法查找给定的数x是否存在数组B中?
提示:同样采用二分查找。核心思想就是确定所查找数所在的范围。通过比较3个数(头,尾,中间)和所查找数之间的关系,可以确定下次查找的范围。
Problem 14:一个排好序的数组A,长度为n,现在将数组A从位置m(m<n,m已知)分开,并将两部分互换位置,设计一个O(n)的算法实现这样的倒置,只允许使用一个额外空间。(循环移位的效率不高)
提示:(A’B’)’ =BA
Problem 15:给出Vector的一个更好实现。(STL的vector内存的倍增的,但是每次倍增需要拷贝已存元素,平均每个元素需要拷贝一次,效率不高)
提示:可使用2^n的固定长度作为每次分配的最小单位,并有序的记录每个块的首地址。这中结构同样可以实现线性查找,并且拷贝代价很低(仅有指针)
Problem 16:给出已排序数组A,B,长度分别为n,m,请找出一个时间复杂度为(lgn)的算法,找到排在第k位置的数。
提示:二分查找。
Problem 17:给出任意数组A,B,长度分别为n,m,请找出一个时间复杂度为(lgn)的算法,找到排在第k位置的数。
提示:通过最小堆记录k个数,不断更新,扫描一次完毕。
这个提示有问题,求最优算法!
Problem 18:假设数组A有n个元素,元素取值范围是1~n,判定数组是否存在重复元素?要求复杂度为O(n)。
法1:使用n的数组,记录元素,存在记为1,两次出现1,即重复。
法2:使用m的数组,分别记录大小:n/m, 2n/m …..的元素个数。桶方法
法3:累加求和。可用于求仅有一个元素重复的方法。
Problem 19:给定排好序的数组A,大小为n,现给定数X,判断A中是否存在两数之和等于X。给出一个O(n)的算法。
提示:从中间向两边查找。利用有序的条件
Problem 20:给定排好序的数组A,大小为n,请给出一个O(n)的算法,删除重复元素,且不能使用额外空间。
提示,既然有重复,必有冗余空间。将元素放入数组的前面,并记录下次可放位置,不断向后扫描即可。
Problem 21:给定两个排好序的数组A,B,大小分别为n,m。给出一个高效算法查找A中的哪些元素存在B数组中。
注意:一般在大数组中执行二分查找,将小数组的元素作为需查找的对象。
更优算法(轩辕刃提供):可以使用两个指针遍历AB,比较当前大小就可以了...时间复杂度o(n+m)
Problem 22:问:有1000桶酒,其中1桶有毒。而一旦吃了,毒性会在1周后发作。现在我们用小老鼠做实验,要在1周内找出那桶毒酒,问最少需要多少老鼠。
答案:10只。将酒编号为1~1000 将老鼠分别编号为1 2 4 8 16 32 64 128 256 512 喂酒时 让酒的编号等于老鼠编号的加和如:17号酒喂给1号和16号老鼠 76号酒喂给4号、8号和64号老鼠 七天后将死掉的老鼠编号加起来 得到的编号就是有毒的那桶酒 因为2的10次方等于1024 所以10只老鼠最多可以测1024桶酒
证明如下:使用二进制表示:01, 10, 100, 1000,… , 1,000,000,000。对于任何一个小于1024的数,均可以采用前面的唯一一组二进制数来表示。故成立。
Problem 23:设计一组最少个数砝码,使得天平能够称量1~1000的重量。
如果砝码只能放单边,1,2 ,4 , 512最好。(只能单加)
如果允许砝码双边放,1, 3, 9, 27…. 最好。(可加可减)已知1,3,如何计算下一个数。现可称重量1,2,3,4。设下个数为x,可称重量为, x-4, x-3, x-2, x-1, x, x+1,x+2, x+3, x+4。为使砝码最好,所称重量应该不重复(浪费)。故x=9。同理,可得后面。
图形算法题
Problem 24:如何判断一个点是否在一个多边形内?
提示:对多边形进行分割,成为一个个三角形,判断点是否在三角形内。
一个非常有用的解析几何结论:如果P2(x1,y1),P2(x2,y2),P3(x3,y3)是平面上的3个点,那么三角形P1P2P3的面积等于下面绝对值的二分之一:
| x1 y1 1 |
| x2 y2 1 | = x1y2 + x3y1 + x2y3 –x3y2 – x2y1 – x1y3
| x3 y3 1 |
当且仅当点P3位于直线P1P2(有向直线P1->P2)的右侧时,该表达式的符号为正。这个公式可以在固定的时间内,检查一个点位于两点确定直线的哪侧,以及点到直线的距离(面积=底*高/2)。
这个结论:可以用来判断点是否在点是否在三角形内。法1:判断点和三角形三边所行程的3个三角形的面积之和是否等于原来三角形的面积。(用了三次上面的公式)。
法2:判断是否都在三条边的同一边,相同则满足,否则不在三角形内。
Problem 25:给出两个n为向量与0点形成角的角平分线。
提示:对两条边进行归一化,得到长度为1的两点,取两个的中点即可。