1. 浪子回头
各个大厂裁员。造成了现在互联网行情不好,形势很严峻啊。有的人说今年是互联网过去十年中最差的一年,也可能是未来十年中最好的一年。身处这样乱世的我们怎么办?我也听很多朋友说,今年的面试都比较严格,特点是"要求高、薪资低"。也经常听见他们说某某大厂考了个手写算法,结果当场挂了。身为程序员的我们,再这样行业形势严峻、竞争压力大的情况下,只有不断提升自身能力,以确保在行业内能有个立足之地。
《数据结构与算法》在我学生时代就是一门让我望而止步的课程。听着名字就感觉很晦涩难懂、需要大量的数学知识做铺垫。相信很多人也都和我一样,上学的时候学的一知半解,到了工作以后也很少用到就不了了之了。但是它却成为了你面试、寻找好的平台的障碍。很多大厂都很看中程序员的基本功,所以在面试中算法就编程了常考题目,为什么呢?因为基础知识就像是一座大楼的地基,它能够决定你技术的高度与深度。所以一般大厂都是看中你有没有这个技术发展的潜力。("所以大家要夯实基本功了。")
在我看来后端程序员应该学的有三大基础知识"数据结构与算法"、"计算机系统"、"操作系统Linux"。在这个人人都必须要手撕算法的时代,彻夜难眠的我(纯属扯淡)决定带领大家一起学习三大基础知识,本次开篇系列是《手撕数据结构与算法》,每一个系列更完就会开启下一个系列,大家不要着急。
先放个图,让大家了解下本系列都要讲的内容

注意,注意前方高能======>(广告植入)
本篇文章已收录到github,点击这里即可访问 后端进阶指南
如果你对我的这个系列感兴趣可以关注我的公众号,带你走上”超神之路、拿高薪offer、当上技术专家、出任个大厂、迎娶白富美、走上人生巅峰,想想还有点小激动。” (请允许我吹个🐂)
来了 来了 他来了 他带着二维码来了!!!
欢迎扫码关注哦!!!
2. 数学知识复习
在我们系统的学习数据结构与算法之前,我们先简单的复习几个数学知识,相信大家也都忘的差不多了,是不是都学完了又还给老师了呢?嫑急,跟我一起来复习一下。
2.1. 指数
指数是幂运算aⁿ(a≠0)中的一个参数,a为底数,n为指数,指数位于底数的右上角,幂运算表示指数个底数相乘。当n是一个正整数,aⁿ表示n个a连乘。当n=0时,aⁿ=1。《百度百科》
指数:就是aⁿ中的n。底数:就是aⁿ的a幂运算:指数个底数相乘。
幂运算公式:

2.2. 对数
 如果a的x次方等于N(a>0,且a不等于1),那么数x叫做以a为底N的对数(logarithm),记作
如果a的x次方等于N(a>0,且a不等于1),那么数x叫做以a为底N的对数(logarithm),记作 。其中,a叫做对数的底数,N叫做真数。《百度百科》
。其中,a叫做对数的底数,N叫做真数。《百度百科》
在计算机科学中,除非有特别的声明,否则所有的对数都是以2为底的。
公式:
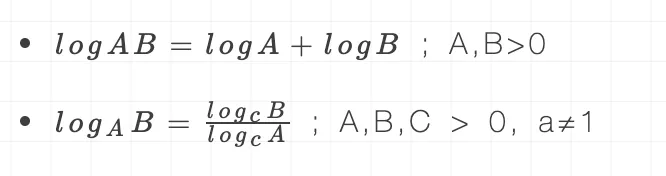
简单列了两个公式,大家看看就行了,知道一下啥是对数。
3. 时间复杂度
对于算法时间复杂度,可能有的朋友可能想了,不就是估算一段代码的执行时间嘛,我们可以搞个监控啊,看看一下每个接口的耗时不就好了,何必那么麻烦,还要分析下时间复杂度。但是这个监控属于事后操作,只有代码在运行时,才能知道你写的代码效率高不高,那么如何在写代码的时候就评估一段代码的执行效率呢,这个时候就需要时间复杂度来分析了。大家平常写代码可以结合时间复杂度和监控做好事前、事后的分析,更好的优化代码。

3.1 大O表示法
因为渐进时间复杂度使用大写O来表示,所以也称大O表示法。例如: O(f(n))。
常见时间复杂度:
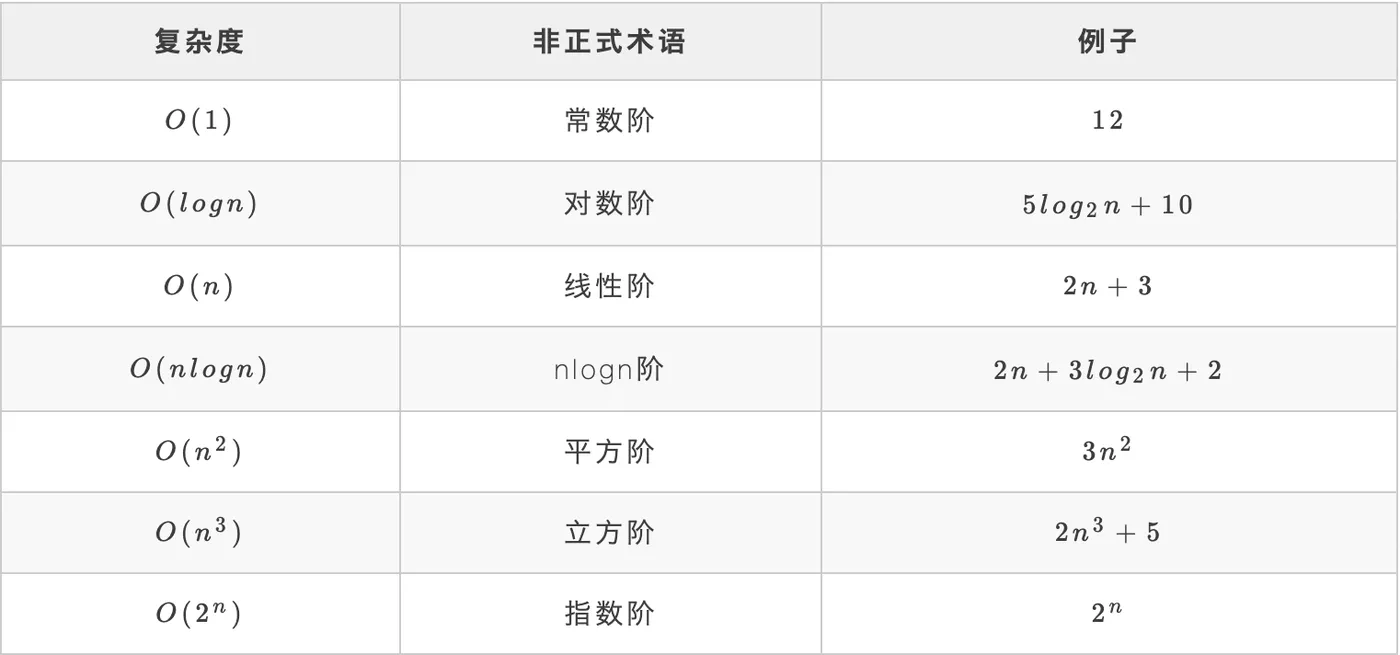
常见时间复杂度所耗费时间从小到大依次是:

推导大O的方法:

3.2 如何分析时间复杂度
O(1)int i = 5; /*执行一次*/
int j = 6; /*执行一次*/
int sum = j + i; /*执行一次*/这段代码的运行函数应该是f(n)=3 ,用来大O来表示的话应该是O(f(n))=O(3) ,但是根据我们的推导大O表示法中的第一条,要用1代替函数中的常数,所以O(3)=>O(1),那么这段代码的时间复杂度就是O(1)而不是O(3)。
O(logn)int count = 1; /*执行一次*/
int n = 100; /*执行一次*/
while (count < n) {
count = count * 2; /*执行多次*/
}
O(n)for (int k = 0; k < n; k++) {
System.out.println(k); /*执行n次*/
}这段代码的执行次数会随着n的增大而增大,也就是说会执行n次,所以他的时间复杂度就是O(n)。

for (int k = 0; k < n; k++) {
for (int l = 0; l < n; l++) {
System.out.println(l); /*执行了n*n次/
}
}
读到这里不知道大家学会了没有?其实分析一段代码的时间复杂度,就找到你代码中执行次数最多的地方,分析一下它的时间复杂度是什么,那么你整段代码的时间复杂度就是什么。以最大为准。
3.3 时间复杂度量级
public int find(int[] arrays, int findValue) {
int result = -1; /*执行一次*/
int n = arrays.length;
for (int i = 0; i < n; i++) {
if (arrays[i] == findValue) { /*执行arrays.length次*/
result = arrays[i];
break;
}
}
return result; /*执行一次*/
}
我们来分析一下上边这个方法,这个方法的作用是从一个数组中查找到它想要的值。其实一个算法的复杂度还会根据实际的执行情况有一定的变化,就比如上边这段代码,假如数组的长度是100,里面存的是1-100的数。
最好情况时间复杂度
如果我在这个数组里面查找数字1,那么在它第一次遍历的时候就找到了这个值,然后就执行
break结束当前循环,此时所有的代码只执行了一次,属于常数阶O(1),这就是最好情况下这段代码的时间复杂度。最坏情况时间复杂度
如果我在这个数组里面查找数字100,那么这个数组就要被遍历一边才能找到并返回,这样的话这个方法就要受到数组大小的影响了,如果数组的大小为n,那么就是n越大,执行次数越多。属于
线性阶O(n),这就是最坏情况下的时间复杂度。平均情况时间复杂度
我们都知道最好、最坏时间复杂度都是在两种极端情况下的代码复杂度,发生的概率并不高,因次我们引入另一个概念
“平均时间复杂度”。我们还看上边的这个方法,要查找个一个数有n+1中情况:在数组0 ~ n-1的的位置中和不再数组中,所以我们将所有代码的执行次数累加起来((1+2+3+…+n)+n),然后再除以所有情况n(n+1),就得到需要执行次数的平均值了。
推导过程:

大O表示法,会省略系数、低阶、常量,所以平均情况时间复杂度是O(n)。
但是这个平均复杂度没有考虑各自情况的发生概率,这里的n+1个情况,它们的发生概率是不一样的,所以还需要引入各自情况发生的概率再具体分析。findValue要么在1~n中,要么不在1~n中,所以他们的概率都是
 ,同时数据在1~n中的各个位置的概率一样为
,同时数据在1~n中的各个位置的概率一样为 ,根据概率乘法法则,findValue在1~n中的任意位置的概率是
,根据概率乘法法则,findValue在1~n中的任意位置的概率是 ,因此在上边推导的基础上需要在加入概率的的发生情况。
,因此在上边推导的基础上需要在加入概率的的发生情况。考虑概率的平均情况复杂度为:

推导过程:
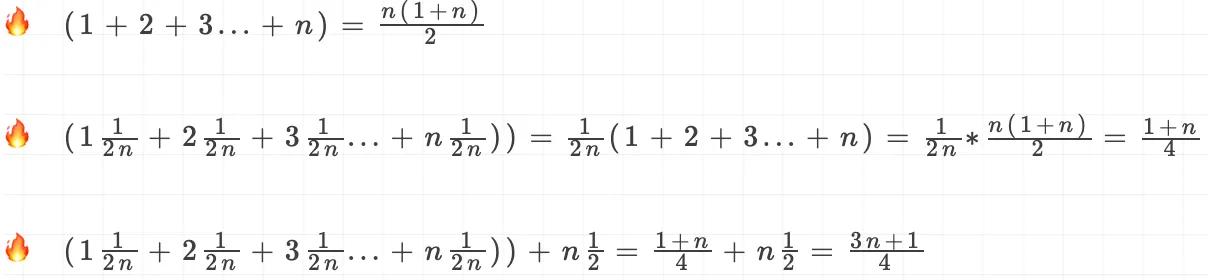
这就是概率论中的加权平均值,也叫做期望值,所以平均时间复杂度全称叫:加权平均时间复杂度或者期望时间复杂度。平均复杂度变为 ,忽略系数及常量后,最终得到加权平均时间复杂度为O(n)。
,忽略系数及常量后,最终得到加权平均时间复杂度为O(n)。
4. 空间复杂度
算法的空间复杂度是对运行过程中临时占用存储空间大小的度量,算法空间复杂度的计算公式记作:S(n) = O(f(n)),n为问题规模,f(n)为语句关于n所占存储空间函数。由于空间复杂度和时间复杂度的大O表示法相同,所以我们就简单介绍下。
常见的空间复杂度从低到高是:

4.1 如何分析空间复杂度
O(1)public static void intFun(int n) {
var intValue = n;
//...
}当算法的存储空间大小固定,和输入的规模没有直接的关系时,空间复杂度就记作O(1),就像上边这个方法,不管你是输入10,还是100,它占用的内存都是4字节。
O(n)public static void arrayFun(int n) {
var array = new int[n];
//...
}当算法分配的空间是一个集合或者数组时,并且它的大小和输入规模n成正比时,此时空间复杂度记为
 。
。
public static void matrixFun(int n) {
var matrix = new int[n][n];
//...
}当算法分配的空间是一个二维数组,并且它的第一维度和第二维度的大小都和输入规模n成正比时,此时空间复杂度记为
 。
。
5. 总结
对于时间和空间的取舍,我们就要根据具体的业务实际情况而定,有的时候就需要牺牲时间来换空间,有的时候就需要牺牲空间来换时间,在现在这个计算机硬件性能飙升的时代,当然我们还是喜欢选择牺牲空间来换时间,毕竟内存还是有的,也不贵。并且可以提高效率给用户更好的体验。
什么是时间复杂度?
时间复杂度就是对算法运行时间长短的度量,用大O表示为
T(n) = O(f(n))。常见的时间复杂度从低到高的顺序是:
什么是空间复杂度?
空间复杂度是对算法运行时所占用的临时存储空间的度量,用大O标识为
S(n)= O(f(n))。常见的空间复杂度从低到高的顺序是:
6. 参考
- 《数据结构与算法分析》
- 《大话数据结构》
- 《漫画算法》
能看到这里的朋友,相信你也对学习保持着一定的热情,觉得对你有帮助的话麻烦点个赞或在看以资鼓励吧,有什么问题欢迎留言或者关注我公众号进群交流。另外文章有理解错误、写错、说错的地方,希望大家指正,这是对我最大的帮助,谢谢大家。




