一、深度优先搜索
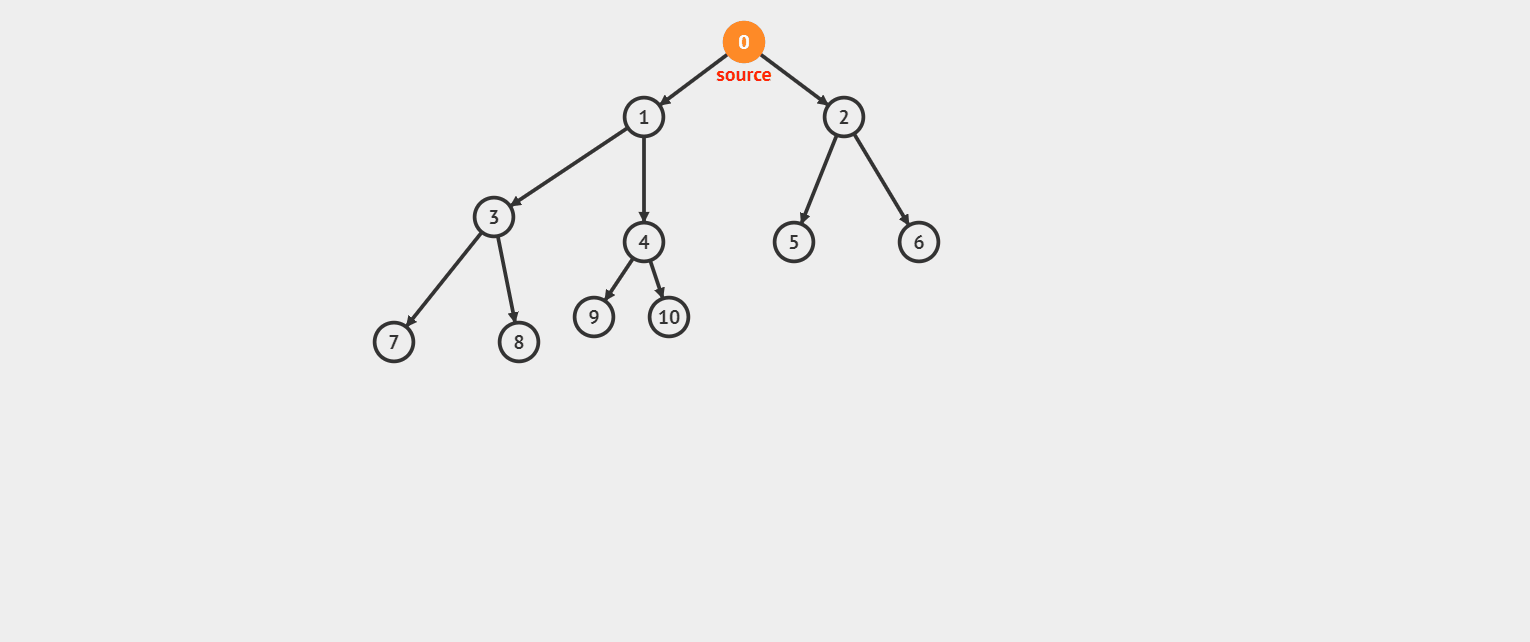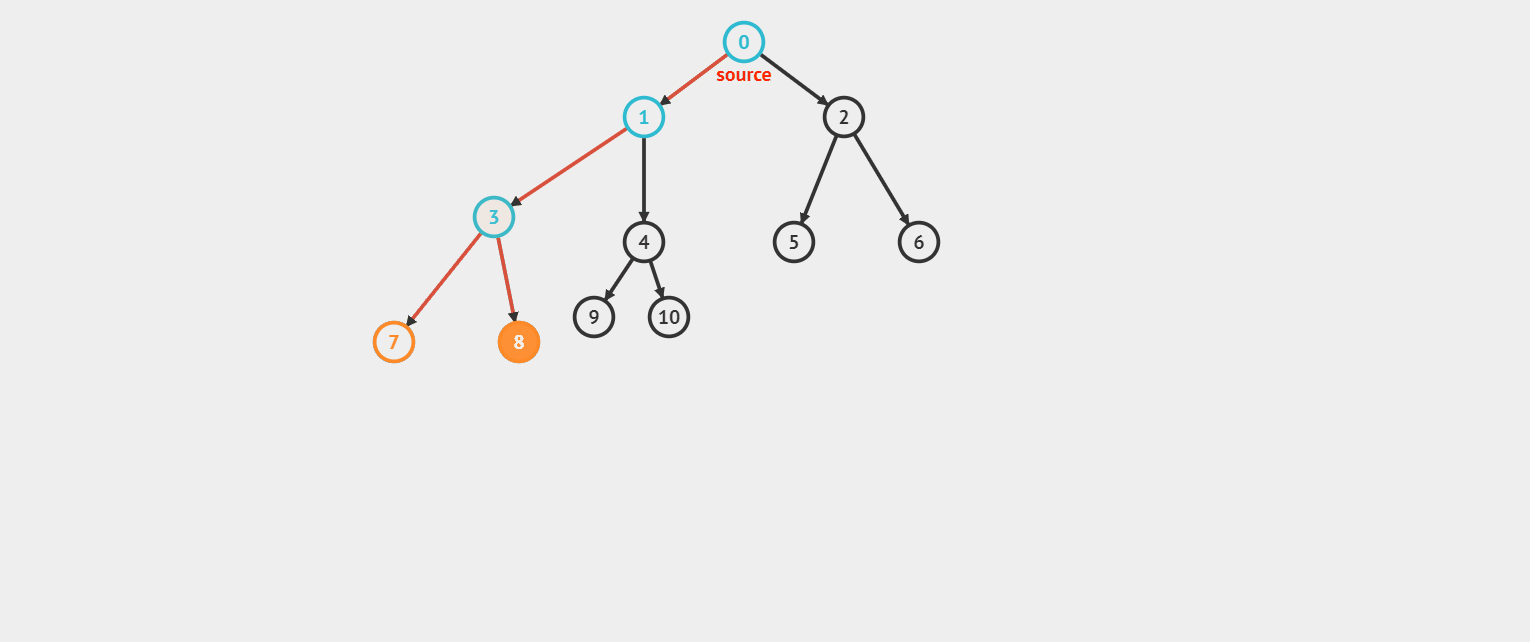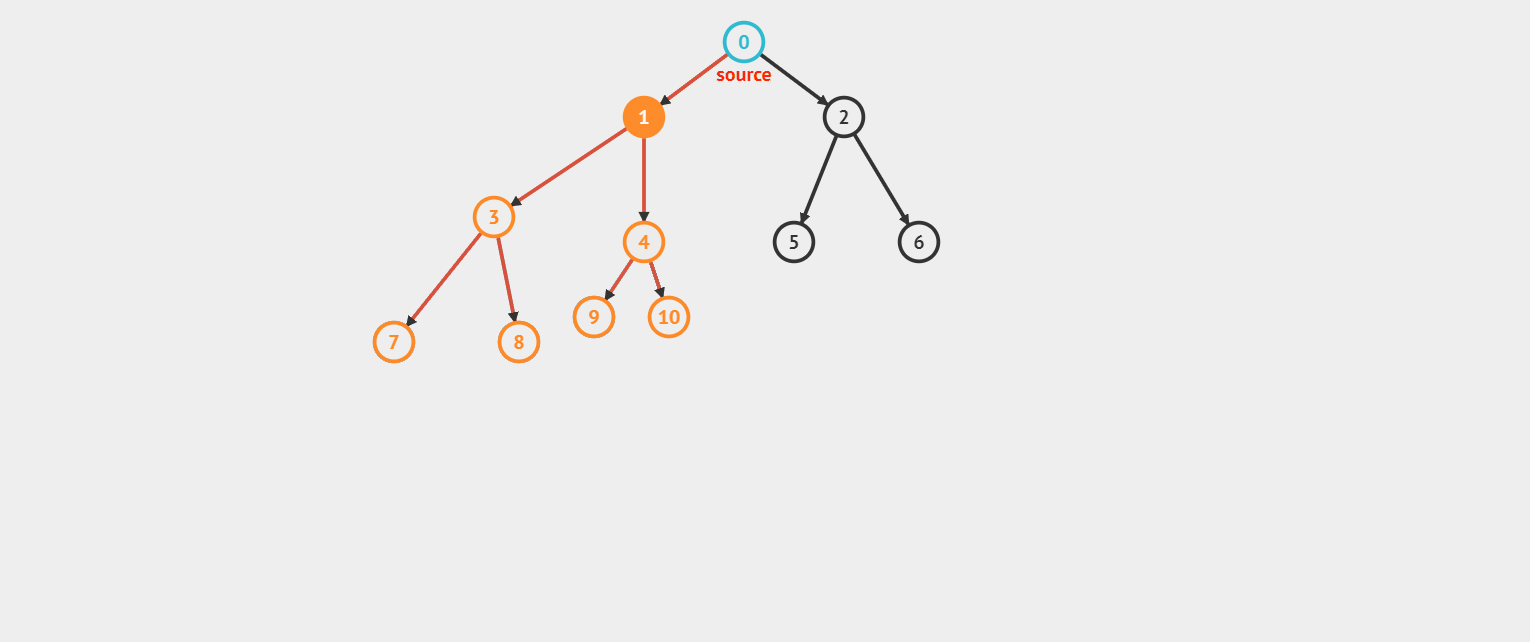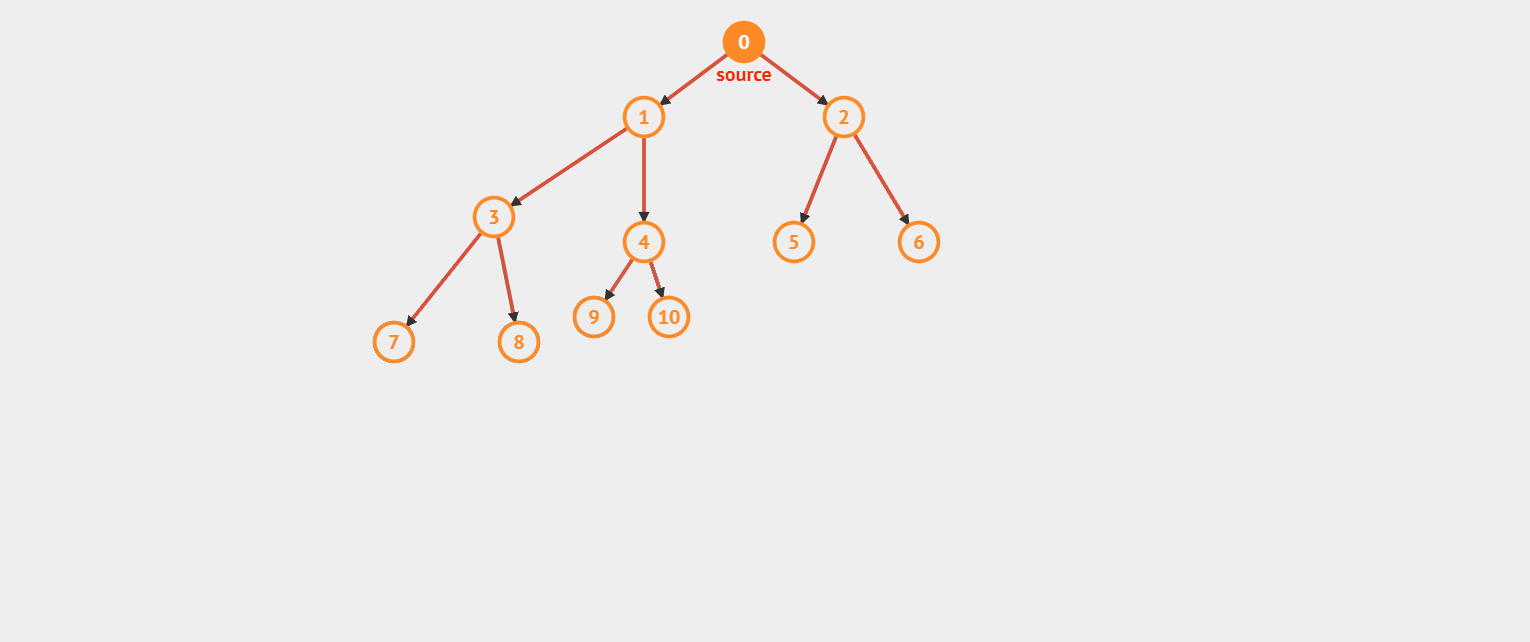
深度优先搜索(DFS)又叫深搜,我们可以这么理解,DFS 像一个很固执的一个人(不撞南墙不回头,不见黄河不死心),只要你这里有路我就一定会去走,而且一条路走到底的那种(燕子~没你我怎么活呀,开玩笑了)。
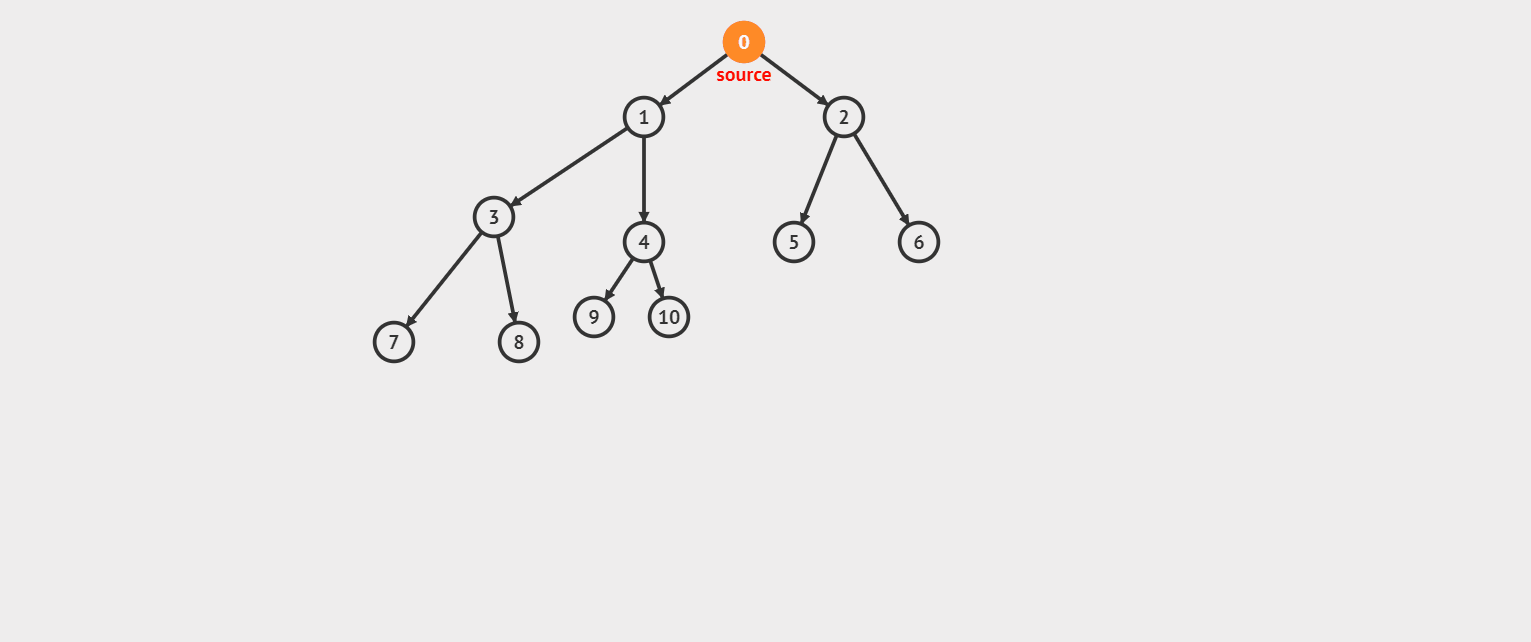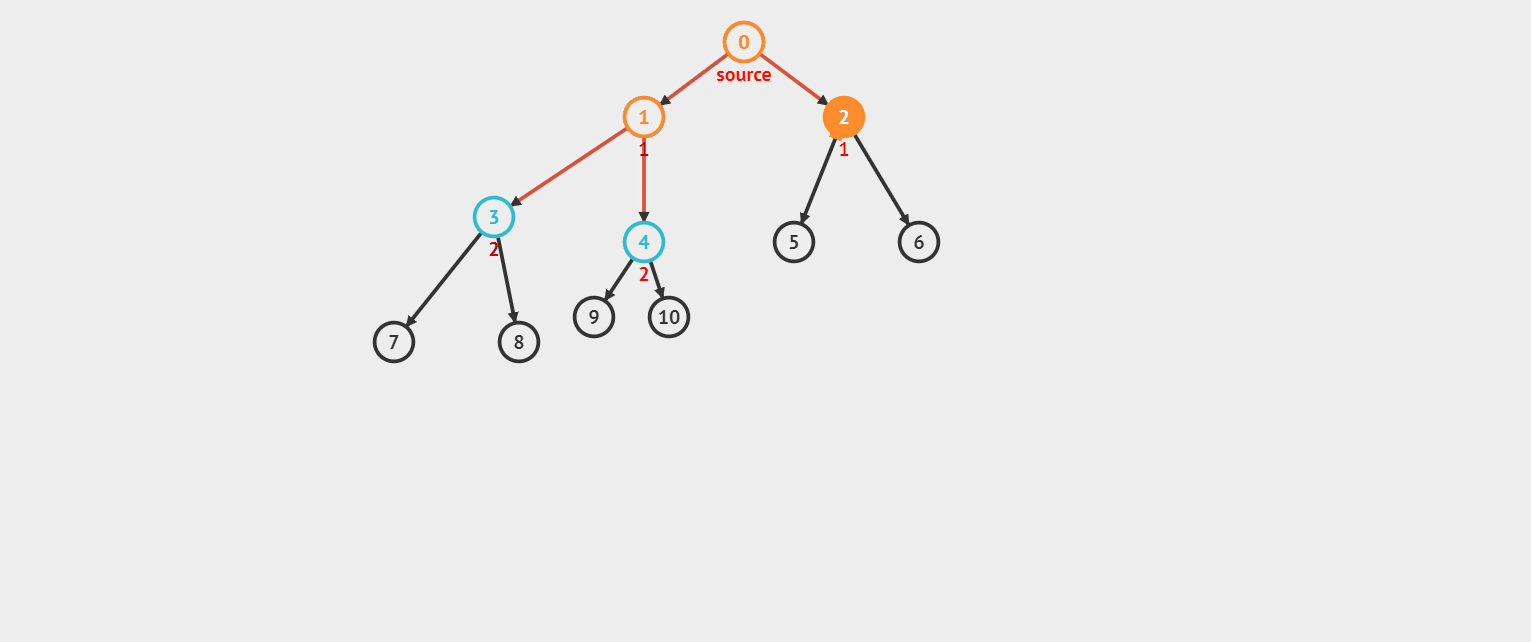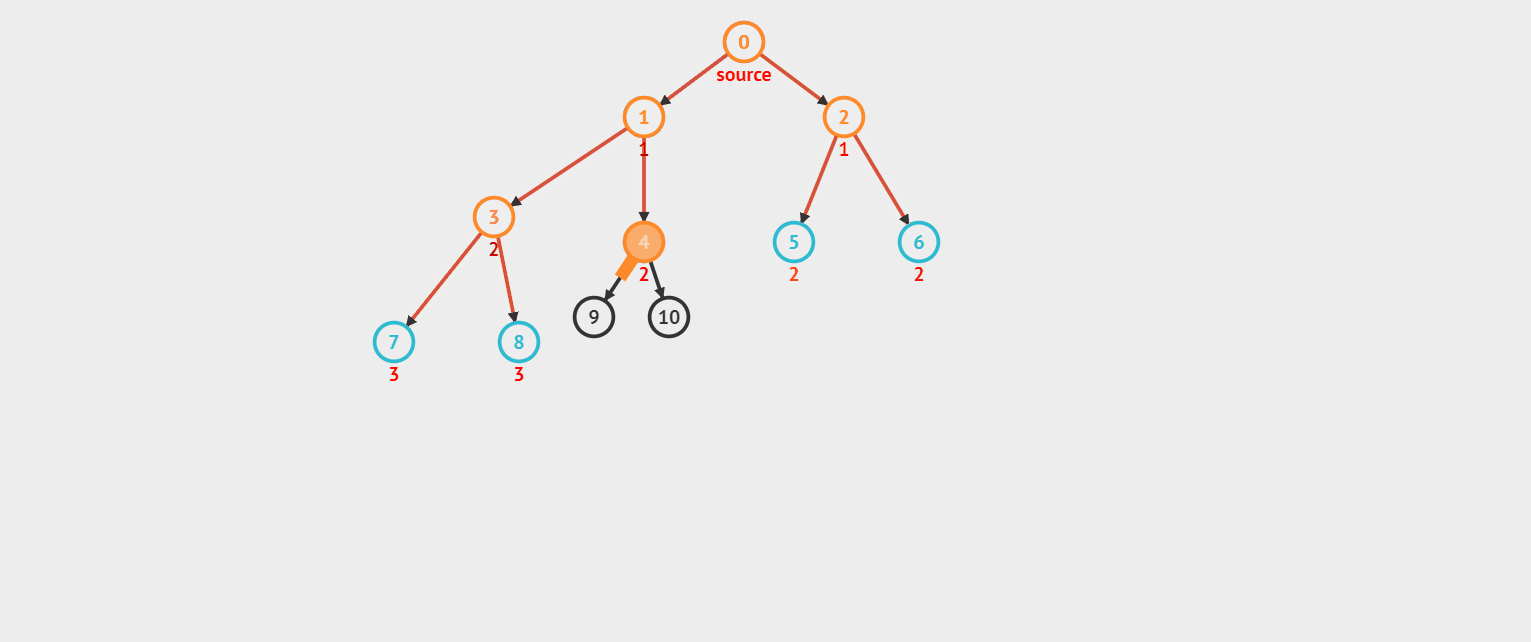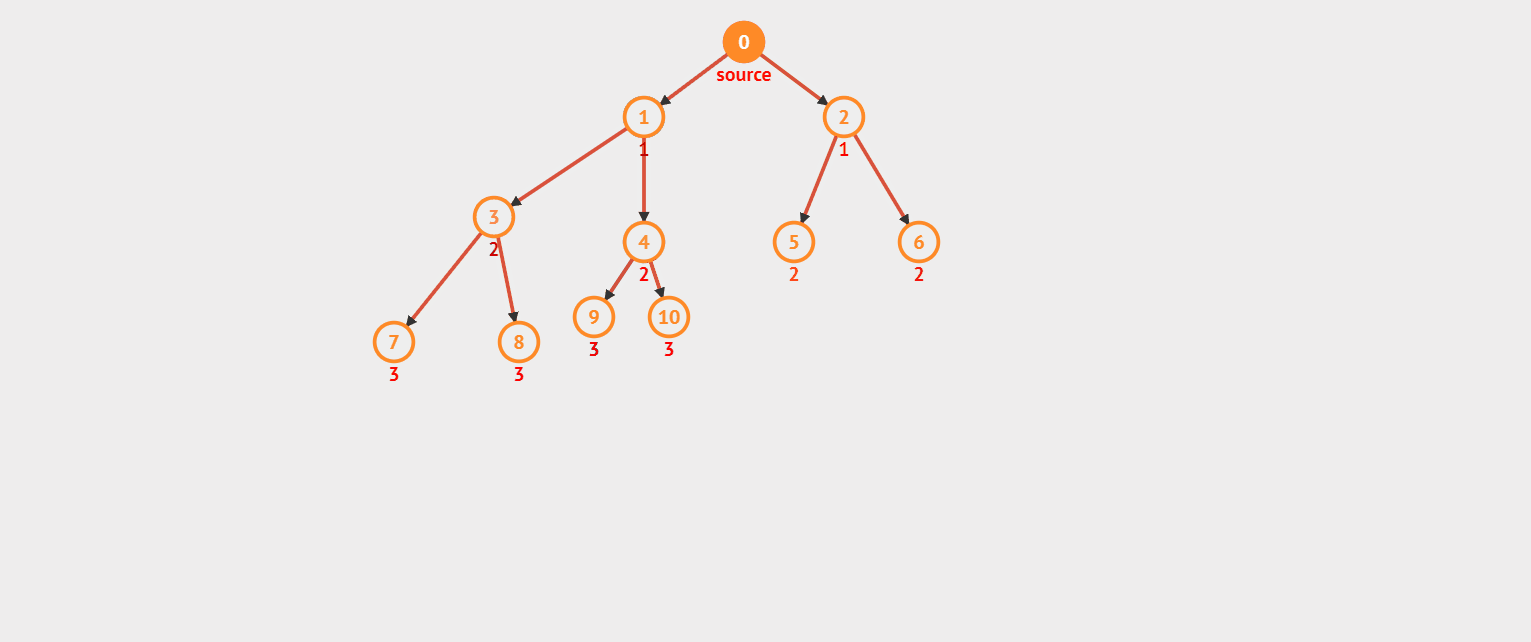
我们先来看看效果图。(对了,上次有小伙伴问,你这效果图是怎么实现的呀,我是在这个网站上绘制效果图的)
看完效果图后感觉是不是挺通俗易懂的?好,我们来看看 DFS 的模板。
dfs(int u) { if(找到了||走不下去了) { return; } 开始下一个情况(dfs(u+1)); }
📸实际问题
我们来看看一个经典的问题——n皇后问题。我们先来看看题目。
给定一个n*n的棋盘,棋盘中有一些位置不能放皇后。
现在要向棋盘中放入n个黑皇后和n个白皇后,使任意的两个黑皇后都不在同一行、同一列或同一条对角线上
任意的两个白皇后都不在同一行、同一列或同一条对角线上。
我们来看看代码
#include <iostream> #include <bits/stdc++.h> using namespace std; typedef long long ll; const int N = 20; int n; char g[N][N]; int l[N],ug[N],ng[N]; void dfs(int u) { if(u == n) { for(int i = 0; i < n; i ++) { cout << g[i] << endl; } cout << endl; return ; } for(int i = 0; i < n; i ++) { if(!l[i] && !ug[i + u] && !ng[i - u + n]) { g[u][i] = 'Q'; l[i] = ug[i + u] = ng[i - u + n] = 1; dfs(u + 1); l[i] = ug[i + u] = ng[i - u + n] = 0; g[u][i] = '.'; } } } int main() { cin >> n; for(int i = 0; i < n; i ++) { for(int j = 0; j < n; j ++) { g[i][j] = '.'; } } dfs(0); return 0; }
二、广度优先搜索
广度优先搜索(BFS)又叫广搜,它像一个有远见的人,它是一层一层来实现搜索的,也挺像下楼梯的。
思路:
1.先初始化队列 q;
2.从起点开始访问,并且改变他的状态为已经访问;
3.如果他的队列非空,取出首个元素,将它弹出!
4.如果u == 目标状态,然后对所以与 u 邻近的点进入队列;
5.标记它已经被访问!
我们先来看看效果图
我们来看看模板
queue<int> q; st[0] = true; // 表示1号点已经被遍历过 q.push(0); while (q.size()) { int t = q.front(); q.pop(); for (int i = h[t]; i != -1; i = ne[i]) { int j = e[i]; if (!s[j]) { st[j] = true; // 表示点j已经被遍历过 q.push(j); } } }
📸实际问题
来看看代码
#include <iostream> #include <bits/stdc++.h> #define x first #define y second using namespace std; const int N = 1000 + 10; int n; typedef pair<int,int> PII; PII q[N * N]; bool st[N][N]; char g[N][N]; int dx[4] = {-1, 0, 1, 0},dy[4] = {0, 1, 0, -1}; void bfs(int sx, int sy, int &tl, int &bd) { int tt = 0,hh = 0; st[sx][sy] = true; q[0] = {sx, sy}; while(hh <= tt) { PII t = q[hh ++]; tl ++; bool is_bd = false; for(int i = 0; i < 4; i ++) { int x = t.x + dx[i],y = t.y + dy[i]; if(x < 0 || x >= n || y < 0 || y >= n || st[x][y]) continue; if(g[x][y] == '.') { is_bd = true; continue; } st[x][y] = true; q[++ tt] = {x, y}; } if(is_bd) bd++; } } int main(){ cin >> n; for(int i = 0;i < n;i++) cin >> g[i]; int cnt = 0; for(int i = 0;i < n;i++) for(int j = 0;j < n;j++) { if(!st[i][j] && g[i][j] == '#') { int tl = 0,bd = 0; bfs(i, j, tl, bd); if(tl == bd) cnt ++; } } cout << cnt << endl; return 0; }
看到这里感觉这么样?对 dfs 与 bfs 有了更新的认识吗?我们接下来再来看看两大算法。
扩展:什么是最小生成树?
给定一个无向图,如果它的某个子图中任意两个顶点都互相连通并且是一棵树,那么这棵树就叫生成树。如果边上有权值,那么使得边权和最小的生成树叫做最小生成树(MST,Minimum Spanning Tree)。
那么下面我们要讲的两大算法就是与最小生成树有关的。
三、prim 算法
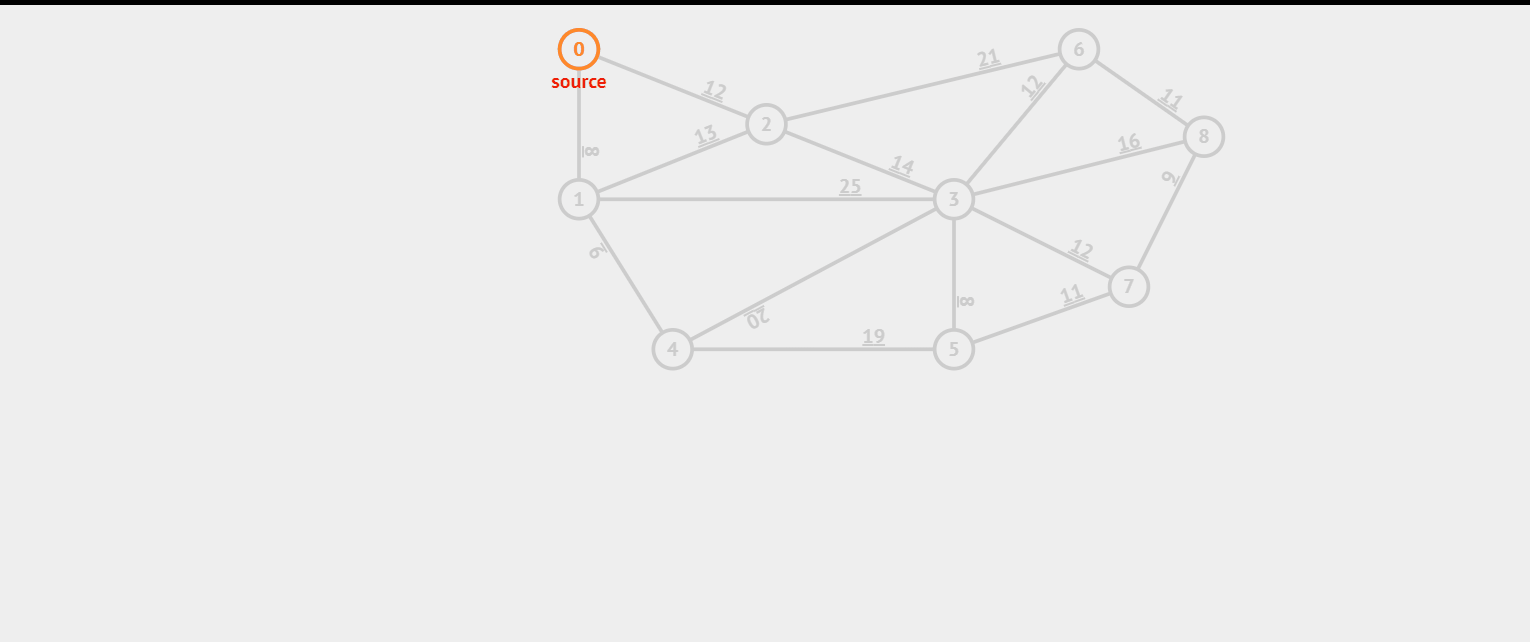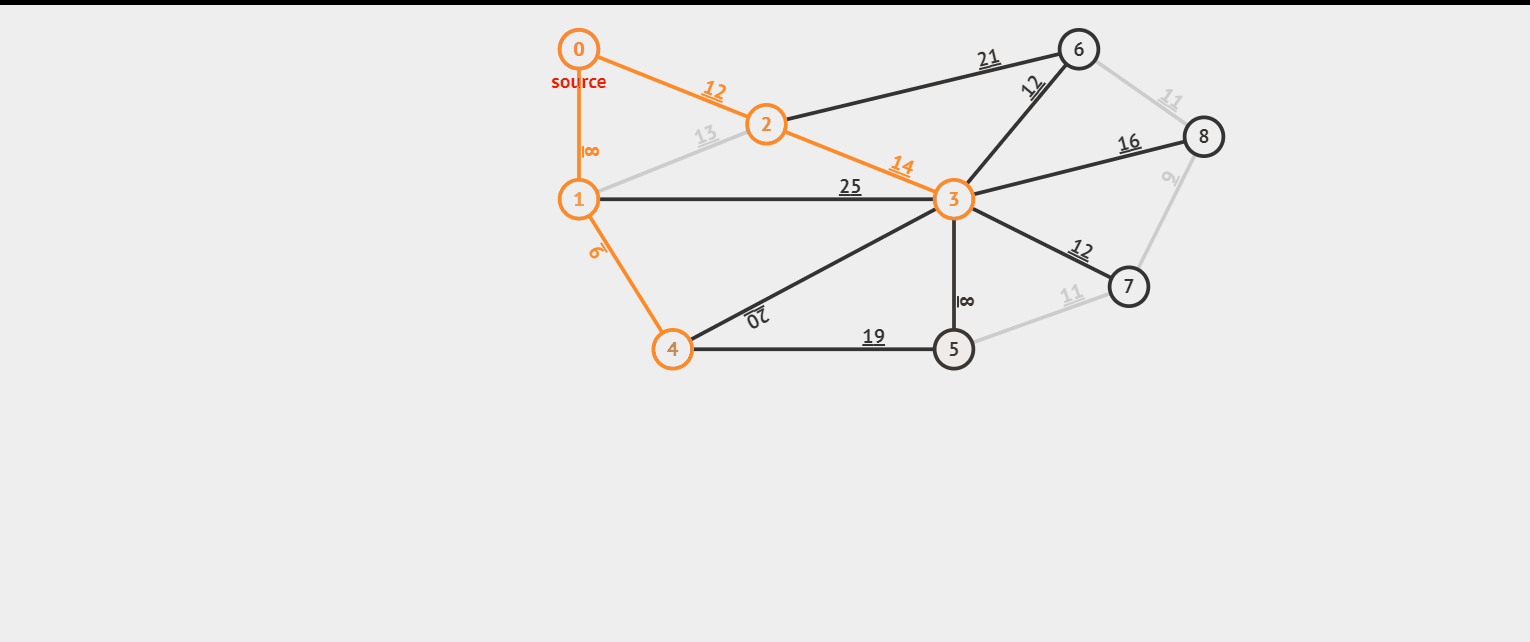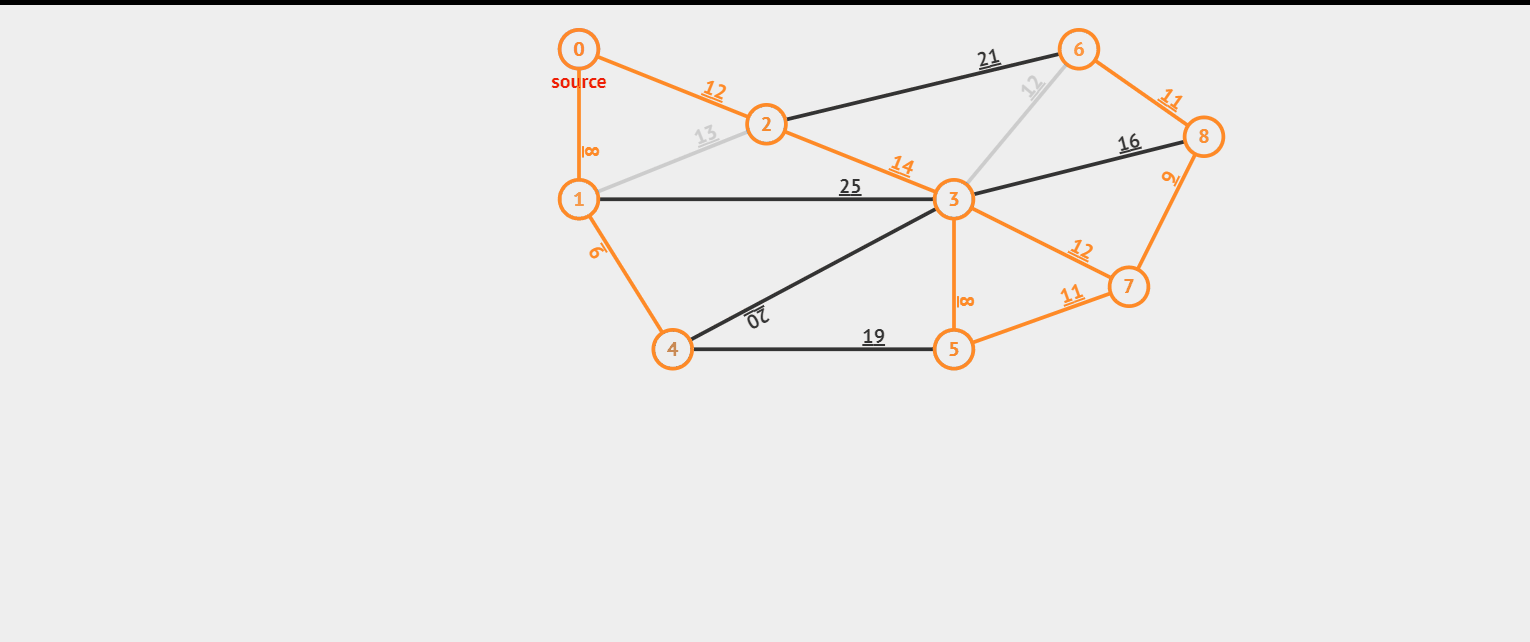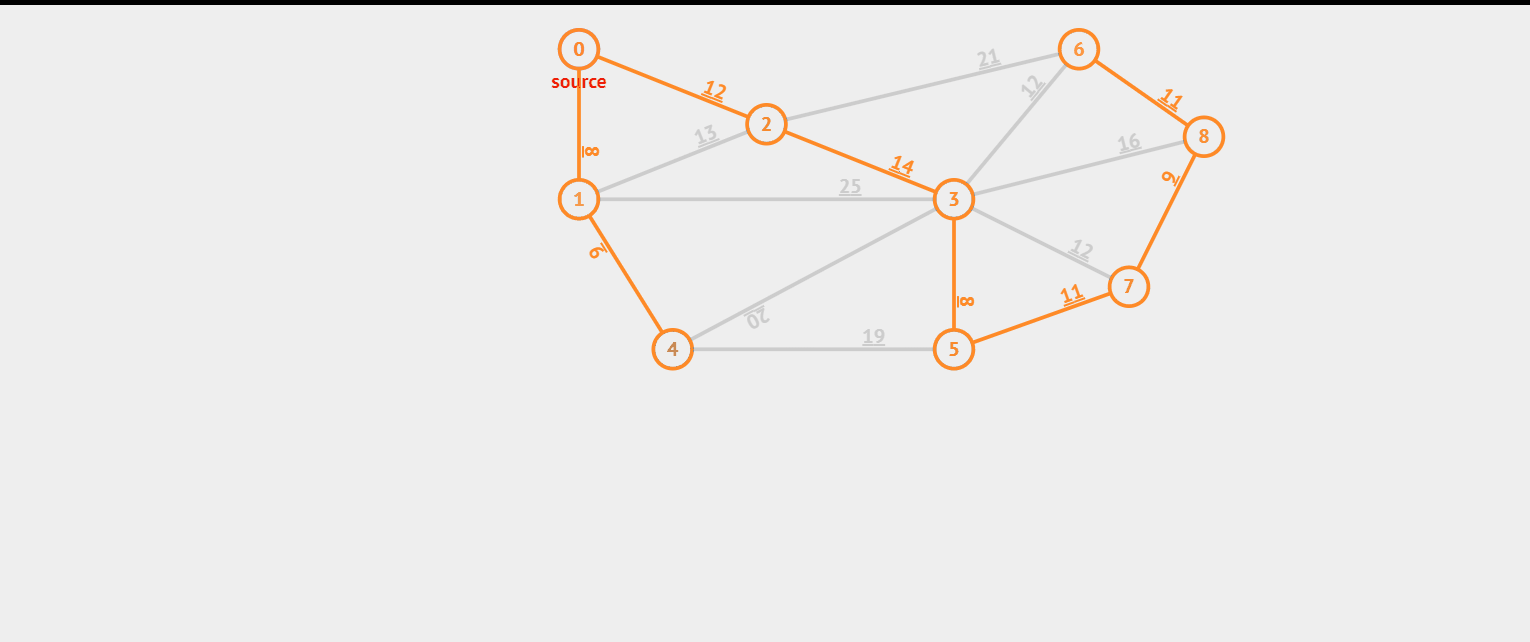
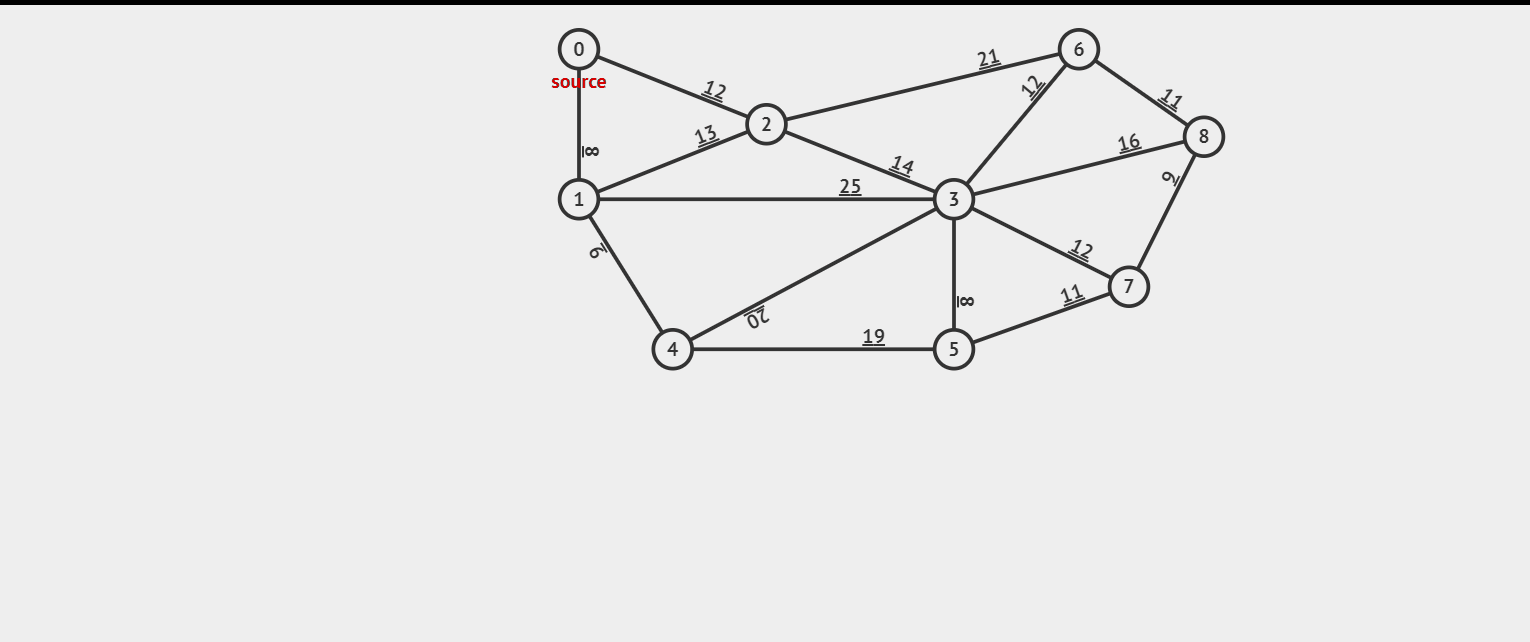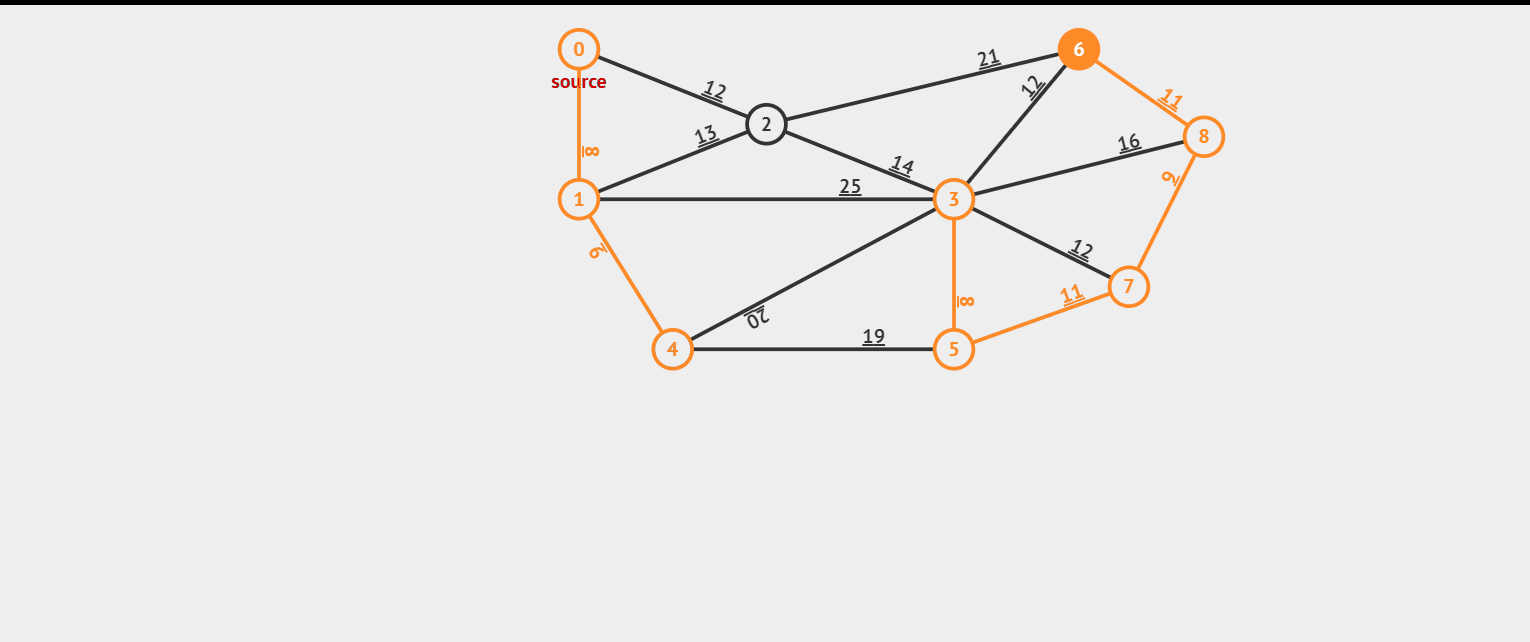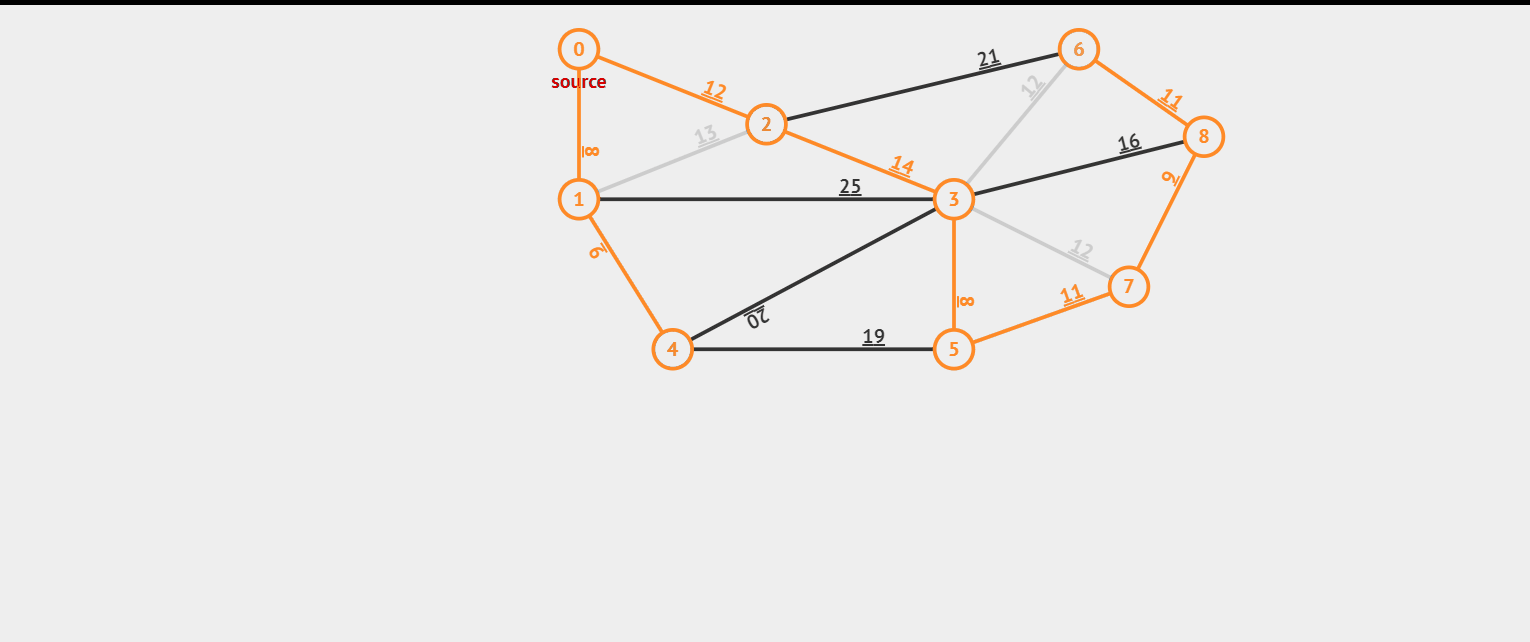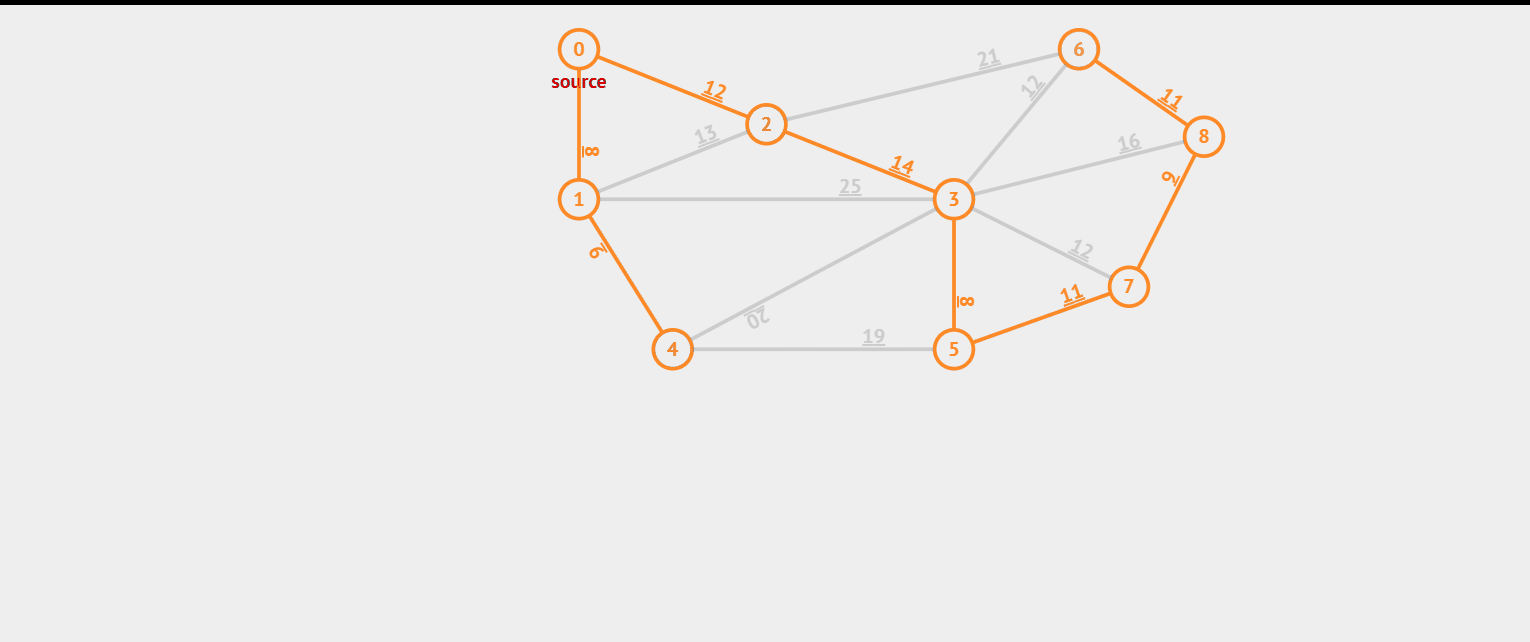
prim 算法也像一个有远见的人,他选择一个节点(假设这个节点上有 n 条边),直接来找这 n 条边上最小的边,然后选择这条最小的边选完之后剩下(n - 1)。再选择连接的最小的边的节点(假设这个节点上有 m 条边)(在 m + n - 1 条边是哪个选择)。选完之后剩下(m + n - 2),依次类推。我们来看看效果图。
算法模板
int prim() { memset(dist, 0x3f, sizeof dist); int res = 0; dist[1] = 0; for(int i = 0; i < n; i ++) { int t = -1; for(int j = 1; j <= n; j ++) if(!st[j] && (t == -1 || dist[j] < dist[t])) t = j; st[t] = true; res += dist[t]; for(int j = 1; j <= n; j ++) if(dist[j] > g[t][j] && !st[i]) { dist[j] = g[t][j]; pre[j] = t; } } return res; }
📸实际题目
给定一个n个点m条边的无向图,图中可能存在重边和自环,边权可能为负数。
求最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
给定一张边带权的无向图G=(V, E),其中V表示图中点的集合,E表示图中边的集合,n=|V|,m=|E|。
由V中的全部n个顶点和E中n-1条边构成的无向连通子图被称为G的一棵生成树,其中边的权值之和最小的生成树被称为无向图G的最小生成树。
这里我们看到上面的效果图,我们可以构成一组数据,如果这组数据没有输出 impossible,那么它存在最小生成树。
9 16 0 1 8 0 2 12 1 4 9 1 3 25 1 2 13 2 6 21 2 3 14 2 6 12 3 5 8 3 7 12 3 8 16 4 5 19 4 3 20 5 7 11 7 8 6 6 8 11
四、Kruskal算法
Kruskal算法它很像一个比较莽撞的人,它直接选择最短的边,只要它满足最小生成树的条件,那么这条边就可行。 我们先来看看效果图。
思路:
①将所有边按权重从小到大排序
②枚举每条边 a,b,权重是c
if a,b不连通
将这条边加入集合
📸实际题目
同样是上面的题目与数据
给定一个n个点m条边的无向图,图中可能存在重边和自环,边权可能为负数。
求最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
给定一张边带权的无向图G=(V, E),其中V表示图中点的集合,E表示图中边的集合,n=|V|,m=|E|。
由V中的全部n个顶点和E中n-1条边构成的无向连通子图被称为G的一棵生成树,其中边的权值之和最小的生成树被称为无向图G的最小生成树。
我们来看看代码是如何实现的。
#include<bits/stdc++.h> using namespace std; const int N = 2e5+5; int n,m; struct Edge { int u, v, w; bool operator<(const Edge &a) const { return w<a.w; } }edge[N]; int p[N]; int find(int x) { return p[x] == x ? x : p[x] = find(p[x]); } int main() { int n, m; scanf("%d%d",&n, &m); for(int i=0;i<m;i++) { int u, v, w; scanf("%d%d%d",&u, &v, &w); edge[i] = {u,v,w}; } sort(edge, edge + m); for(int i = 1; i <= n; i ++) p[i] = i; int cnt = 0, sum = 0; for(int i = 0; i < m; i ++) { int a = edge[i].u, b=edge[i].v, w = edge[i].w; a = find(a); b = find(b); if(a != b) { cnt ++; sum += w; p[a] = b; } } if(cnt < n - 1) puts("impossible"); else printf("%d", sum); }
用同样的数据,不同的算法得到相同的结果,没毛病。
五、小结
我们来看看时间复杂度的分析
BFS的复杂度分析
最坏的情况下,空间复杂度为O(v)。
每个顶点均需搜索一次,时间复杂度T1=O(v),每条边至少访问1次,时间复杂度为O(E),算法总的时间复 度为O(|V|+|E|)。
查找每个顶点的邻接点所需时间为O(V),即该节点所在的该行该列。又有n个顶点,故算总的时间复杂度为O(|V|^2)。
DFS复杂度分析
它的空问复杂度为O(V)。
查找所有顶点的邻接点所需时间为O(E),访问顶点的邻接点所花时间为O(V),此时,总的时间复杂度为O(V+E)。
查找每个顶点的邻接点所需时间为O(V),要查找整个矩阵,故总的时间度为O(V^2)。
注意: v为图的顶点数,E为边数。
算法对程序员来说及其重要,语言和开发平台不断变化,但是万变不离其宗的是那些算法和理论,依稀记得我那个玩的很好的一个学长(在大二就拿到了 offer),他告诉我想找一个好的工作,那刷题一定是必不可少的
现在算法刷题平台还是蛮多的,给大家介绍一个我认为与大厂关联最深的平台——牛客网