自动控制基础基础实验
实验一 典型环节的电路模拟与仿真
实验目的
通过各种典型环节[比例( p )环节、惯性环节、比例微分(PD)环节、比例积分(PI) 环节、积分(I)环节、比例积分微分(PID)环节]的设计,熟悉MATLAB软件仿真开发环境,掌握典型环节设计的流程,完成各种典型环节软件仿真模拟电路的阶跃特性测试,并研究参数变化对典型环节阶跃特性的影响。
实验器材
MATLAB
实验内容
完成各种典型环节的阶跃特性测试,并研究参数变化对典型环节阶跃特性的影响。包括比例( P )环节、惯性环节、比例微分(PD)环节、比例积分(PI) 环节、积分(I)环节、比例积分微分(PID)环节。
打开实验环境
打开MATLAB,点击Simulink,在Simulink里新建一个Blank Model.


点击完blank model后得到下面界面

1) 比例环节
==原理:==
比例积分环节的时域图如下:
比例环节的微分方程为:
$$ c(t)=K*e(t) $$
比例环节传递函数为:
$$ G(s)=K$$
故单位阶跃响应为:
==实操:==
在以上界面我们建立如下原理图:
点击运行按钮后,双击scope将会显示图像如图:

我设置的阶跃函数x=1开始,幅值为1,后面例子都是如此,就不再赘述。
参数K对比例环节的影响:
原理图按下图连接:
scoop得到的图像为:
ps: 后续单一变量的scoop图像都以黑色为底色,观察参数影响的scoop图以白色为底色.
分析:根据scope图像显示,我们可以得到一个从1开始,幅值为2的阶跃函数。此处对应比例环节。即为初始阶跃信号乘上比例系数2得到的信号。
2)惯性环节
==原理:==
惯性环节极点图:
惯性环节的微分方程为:
惯性环节传递函数为:
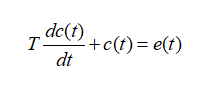
故单位阶跃响应为:
==实操:==
构建如下原理图:
运行后点击scope得到如下图像:

参数T对惯性环节的影响:
构建如下原理图:
scoop图为:

分析:根据scope图像显示,我们可以更好地理解什么是惯性环节,惯性环节的输出一开始并不与输入同步按比例变化,而是直到过渡过程结束,y(t)才能与x(t)保持比例,所以我们发现,系统稳定时,输出为1。与输入的阶跃信号重合。我们可以辅以电容充电过程理解,当电容两端开始接上电压时(初始状态为0),充电过程不是瞬间完成的,需要时间Δt。即为充电过程,充电完毕后才能达到两端接口电压值。
==且T越大,信号达到稳态时间越长。==
3)比例微分(PD)环节
==原理:==
比例微分环节阶跃特性:
比例微分环节的微分方程为:
比例微分环节的传递函数为:

故单位阶跃响应为:
==实操:==
构建如下原理图:
运行后点击scope得到如下图像:

参数KD不变时,参数Kp变化对比例微分环节阶跃特性的影响:
按下图连接:
==上述每一个操作块都为下图的结构==

scoop图像为:
参数Kp不变时,参数KD变化对比例微分环节阶跃特性的影响:
scoop图像为:

分析:根据scope图像显示,我们从原理图上可以看到这么一个模块Δu/Δt,这个模块作为微分环节,字面意思即为求微分,而阶跃信号,求微分时只在转折点处,此处即为x=1处。阶跃信号求导,其导数趋向于∞。比例积分即微分加上比例环节。这就与我们的理论知识阶跃函数在转折点处导数为冲击函数,冲击函数在图像上的表现即为一条高度趋向于∞,宽度趋向于0的矩形。(即为无限高的射线)
4)比例积分(PI) 环节
==原理:==
比例积分环节阶跃特性:
比例积分环节的微分方程为:

比例积分环节的传递函数为:

故单位阶跃响应为:
==实操:==
构建如下原理图:
运行后点击scope得到如下图像:

参数KI不变时,参数Kp变化对比例积分环节阶跃特性的影响:
构建如下原理图:

scoop图像为:

参数Kp不变时,参数KI变化对比例积分环节阶跃特性的影响:
构建如下原理图:

分析: 根据scope图像显示,我们发现结果为阶跃信号加上一个斜坡信号,其中斜坡信号即为积分环节,两者结合即为比例积分环节。仔细观察可以得到图像的斜线开始与x=1,y=1点,即为上述的阶跃信号加上斜坡信号。(斜坡信号即为阶跃信号的积分)
5)积分(I)环节
==原理:==
积分环节阶跃特性:
积分环节的微分方程为:

积分环节的传递函数为:

故单位阶跃响应为:

==实操:==
构建如下原理图:
运行后点击scope得到如下图像:

参数T变化对积分环节阶跃特性的影响:
构建如下原理图:

scoop图像:

分析:根据scope图像显示,我们发现结果为斜坡信号,即阶跃信号的积分。且T越小,积分作用越明显。
6)比例积分微分(PID)环节
==原理:==
比例积分微分环节阶跃特性:

比例积分微分环节的微分方程为:
积分环节的传递函数为:
故单位阶跃响应为:
==实操:==
构建如下原理图:

运行后点击scope得到如下图像:

参数KI、KD不变时,参数Kp变化对比例积分微分环节阶跃特性的影响:
构建如下原理图:

scoop图像为:

参数Kp、KD不变时,参数KI变化对比例积分微分环节阶跃特性的影响:
scoop图像为:
参数Kp、KI不变时,参数KD变化对比例积分微分环节阶跃特性的影响:

分析:据scope图像显示,我们发现结果为上面三个实验的叠加,比如比例环节就是对幅值的一个影响。微分即会产生一个冲击信号,积分环节生成一个斜坡信号,当然上述的结果都是在输入信号为阶跃信号的前提下。
PID在我们自动化中非常重要,我们通过对比例、微分、积分三个环节进行系数占比的调整,可以得到令我们满意的结果。
总结
上述实验内容即为体会各种典型环节,通过观看输出的图像,以及分析结果来理解各环节的作用。
*ps:上述为我个人觉得比较典型的环节的仿真与分析。后续实验在另一篇文章内!*
🙆==如果想要相应的报告可以评论或私信联系我!==🙆♂️

