【算法】自由下落的距离计算

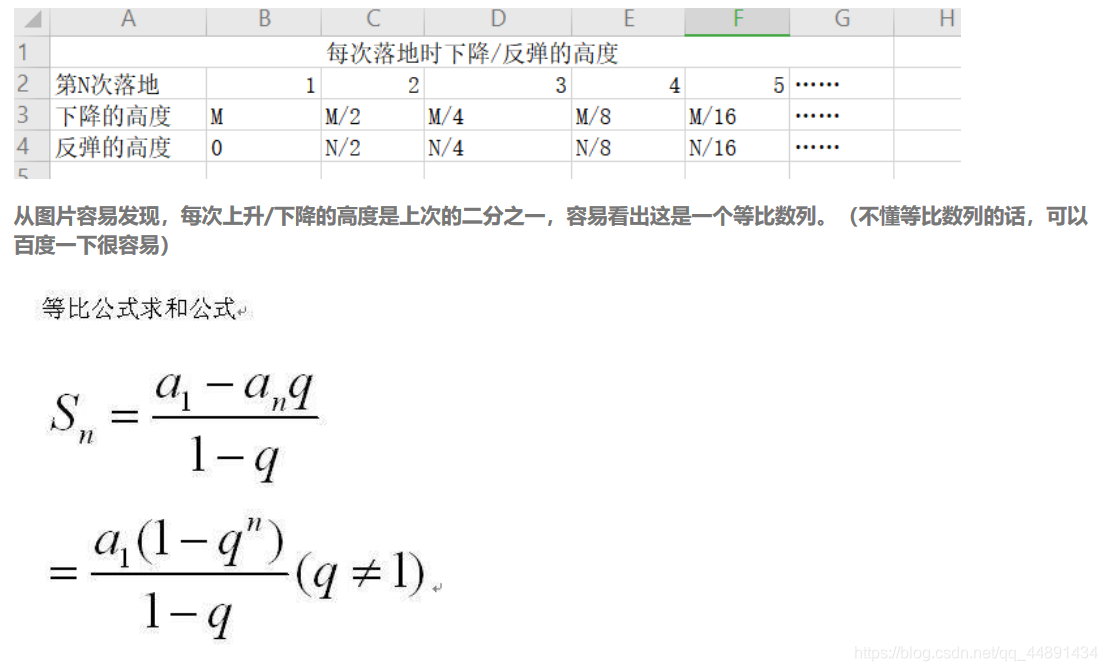
一球从M米高度自由下落，每次落地后返回原高度的一半，再落下。 它在第N次落地时反弹多高？共经过多少米？ 保留两位小数

1. 第N次下落时反弹所得的高度很容易得到，每次反弹是上一次的1/2，第N次就是第一次的（1/2）^N.
2. 接下来分析如何求得第N次落地总共经历的高度。为了得到发现规律，简化算法，我们可以把过程分为两部分来求：
   经过的总路程=球下落的总路程+上升的总路程。
   根据等比数列求和公式，可知N次落地时：
   下路的总路程之和=M(1-0.5^{N)/0.5=2M(1-0.5}N)
   上升的总路程之和=M/2(1-0.5^{(N-1))/0.5=M(1-0.5}(N-1))
   这里唯一需要注意的就是，上升路程计算公式1-0.5^（N-1），这是因为第一次落地的时候，还没有反弹，上升高度为零。
   代码：

#include<stdio.h>
#include<math.h>
int main(){
  double m,n;
  double s,x;//分别用来计算上升/下降的总路程 
  scanf("%lf %lf",&m,&n);
  s = m*(1-pow(1.0/2.0,n-1)); //计算上升的总路程
  x = 2*m*(1-pow(1.0/2.0,n));//计算下降的总路程
  printf("%.2lf %.2lf",m*pow(1.0/2.0,n),s+x);
  return 0;
}