文章目录

排序

常见的排序算法

常见排序算法的实现

选择排序最慢排序（最好理解）所以搬血

基本思想：

每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

直接选择排序

在元素集合array[i]–array[n-1]中选择关键码最大(小)的数据元素

若它不是这组元素中的最后一个(第一个)元素，则将它与这组元素中的最后一个（第一个）元素交换

在剩余的array[i]–array[n-2]（array[i+1]–array[n-1]）集合中，重复上述步骤，直到集合剩余1个元素

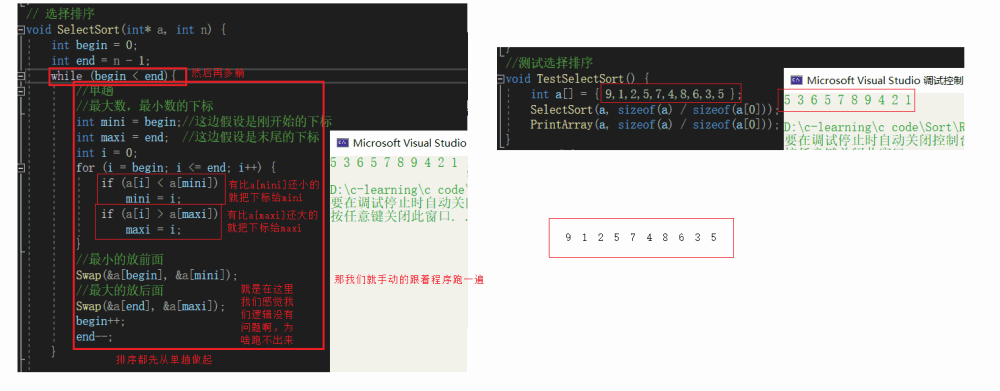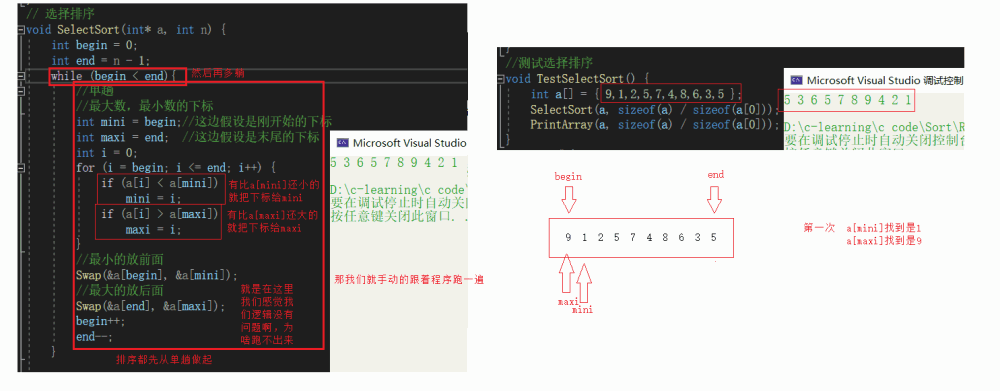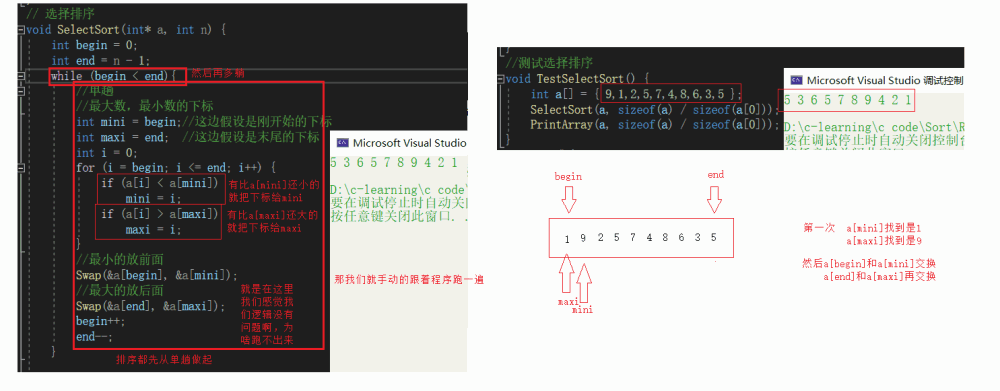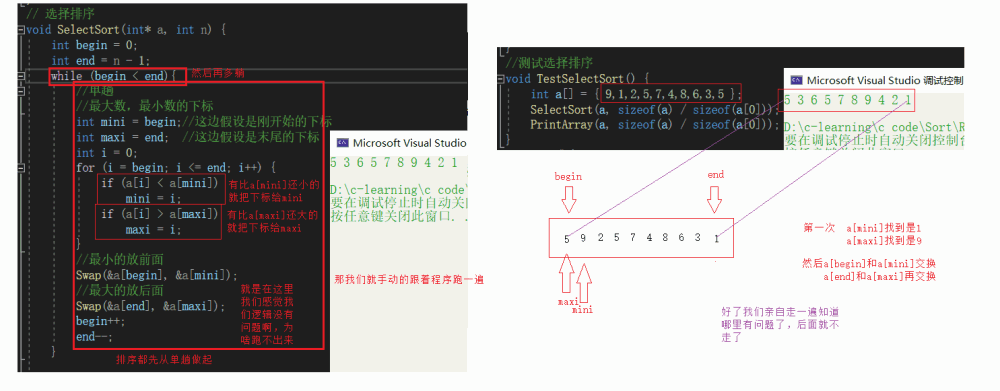
上面那个就是选择排序的本质，但是一次就选一个最大或者最小是不是有点浪费，我们一次同时选到最大最小，就是会比传统的选择排序快一倍

我们基本看到上面代码的缺陷就是我们第一个就是最大是时候，最大的就被换走了，而最小的就被换过来了，但是最大的下标还是标记首位置，把最小的换到后面，也就出现了最小的1在后面的现象

解决方法：既然你最大数的下标和begin重合，那最大数被换走的时候，maxi这个下标也要连带着走

实际上下面才是我第一次写的代码，直接说下次我再也不写装逼的交换了

我来道bug恶心之处看好了跳跳 5 ^ 5 == 0 这就是恶心之处，下次再也不装逼了

数据交换剥离出来其他函数也会用到我明明是简洁之人为了一时的高级而忘记了朴素罪过罪过

//数据交换
void Swap(int* pa, int* pb) {
  int tmp = *pa;
  *pa = *pb;
  *pb = tmp;
}

选择排序

// 选择排序
void SelectSort(int* a, int n) {
  int begin = 0;
  int end = n - 1;
  while (begin < end){
    //单趟
    //最大数，最小数的下标
    int mini = begin;//这边假设是刚开始的下标
    int maxi = end;  //这边假设是末尾的下标
    int i = 0;
    for (i = begin; i <= end; i++) {
      if (a[i] < a[mini])
        mini = i;
      if (a[i] > a[maxi])
        maxi = i;
    }
    //最小的放前面
    Swap(&a[begin], &a[mini]);
    if (begin == maxi)
      //如果最大数就是begin位置的，那么交换的时候最大数连带着下标一起动
      maxi = mini;
    //最大的放后面
    Swap(&a[end], &a[maxi]);
    begin++;
    end--;
  }
}

时间复杂度是O(N²) 我们的优化不是质的优化，而是量的优化

最好：O(N²)

最坏：O(N²)

堆排序

堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。它是

通过堆来进行选择数据。需要注意的是排升序要建大堆，排降序建小堆。

向下调整函数

//向下调整函数
void AdjustDown(int* a, int n, int parent)
{
  assert(a);
  //创建一个孩子变量，有两个孩子就在这个上加1就行
  int child = parent * 2 + 1;
#if HEAP
  while (child < n)
  {
    //选大孩子
    if (child + 1 < n && a[child] < a[child + 1])
    {
      child++;
    }
    //大的孩子还大于父亲就交换
    if (a[child] > a[parent])
    {
      Swap(&a[child], &a[parent]);
      parent = child;
      child = parent * 2 + 1;
    }
    else
    {
      break;
    }
  }
#elif !HEAP
  while (child < n)
  {
    //选小孩子
    if (child + 1 < n && a[child] > a[child + 1])
    {
      child++;
    }
    //小的孩子还小于父亲就交换
    if (a[child] < a[parent])
    {
      Swap(&a[child], &a[parent]);
      parent = child;
      child = parent * 2 + 1;
    }
    else
    {
      break;
    }
  }
#endif // HEAP  
}

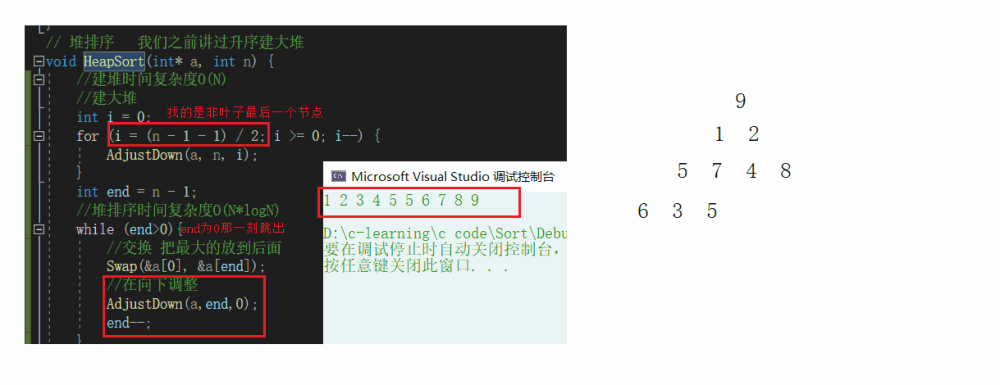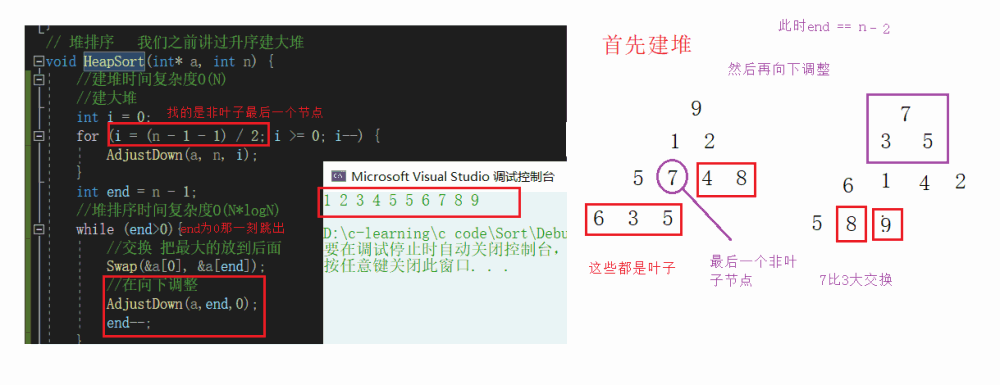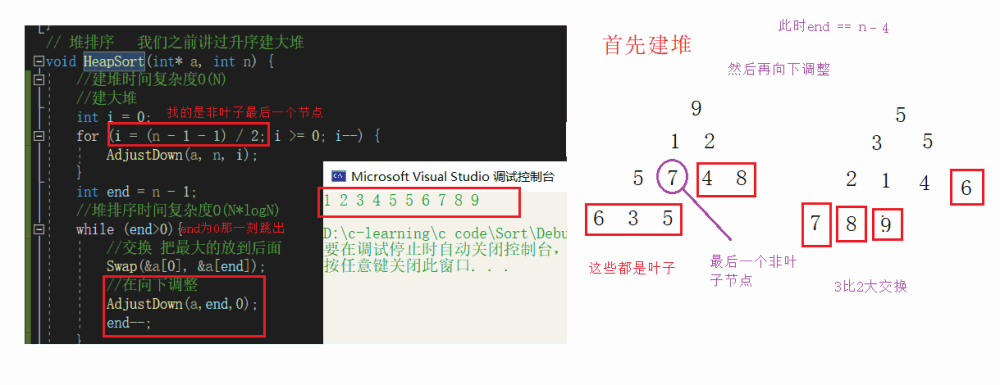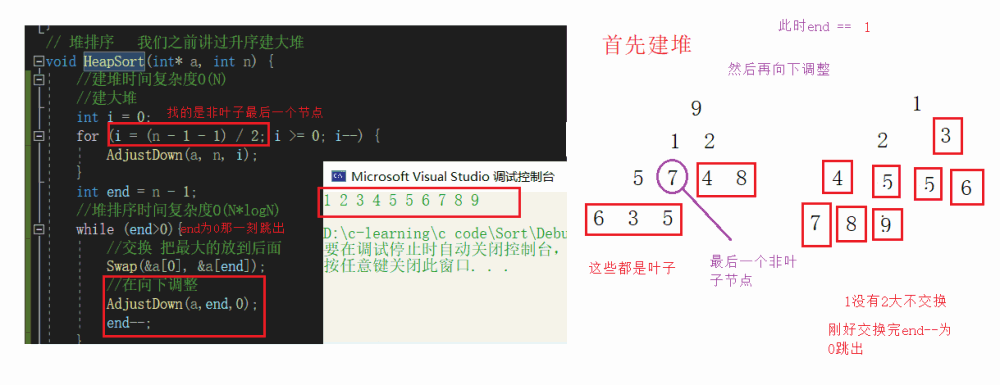
堆排序代码

// 堆排序   我们之前讲过升序建大堆
void HeapSort(int* a, int n) {
  //建堆时间复杂度O(N)
  //建大堆
  int i = 0;
  for (i = (n - 1 - 1) / 2; i >= 0; i--) {
    AdjustDown(a, n, i);
  }
  int end = n - 1;
  //堆排序时间复杂度O(N*logN)
  while (end>0){
    //交换 把最大的放到后面
    Swap(&a[0], &a[end]);
    //在向下调整
    AdjustDown(a,end,0);
    end--;
  }
}

堆排序时间复杂度O(N*logN)

测性能让你看看什么叫堆

这里我们测性能就用release版本测吧因为release版本是程序最优状态，每个排序都是最好状态，巅峰打巅峰

1000大小数组一千

10000大小数组一万

100000大小数组十万

1000000大小数组一百万

10000000大小数组一千万我们不带选择，插入玩太拉跨了，我们看看希尔，堆在超大数据面前谁性能更优

性能函数图

代码

Sort.h

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <time.h>
#define HEAP        1
// 排序实现的接口
// 打印数组
extern void PrintArray(int* a, int n);
// 插入排序
extern void InsertSort(int* a, int n);
// 希尔排序
extern void ShellSort(int* a, int n);
//数据交换
extern void Swap(int* pa, int* pb);
// 选择排序
extern void SelectSort(int* a, int n);
//向下调整
extern void AdjustDwon(int* a, int n, int parent);
// 堆排序
extern void HeapSort(int* a, int n);
// 冒泡排序
extern void BubbleSort(int* a, int n);
// 快速排序递归实现
// 快速排序hoare版本
extern int PartSort1(int* a, int left, int right);
// 快速排序挖坑法
extern int PartSort2(int* a, int left, int right);
// 快速排序前后指针法
extern int PartSort3(int* a, int left, int right);
extern void QuickSort(int* a, int left, int right);
// 快速排序 非递归实现
extern void QuickSortNonR(int* a, int left, int right);
// 归并排序递归实现
extern void MergeSort(int* a, int n);
// 归并排序非递归实现
extern void MergeSortNonR(int* a, int n);
// 计数排序
extern void CountSort(int* a, int n);

Sort.c

#define _CRT_SECURE_NO_WARNINGS 1
#include "Sort.h"
// 打印数组
void PrintArray(int* a, int n) {
  assert(a);
  int i = 0;
  for (i = 0; i < n; i++) {
    printf("%d ", a[i]);
  }
  printf("\n");
}
// 插入排序
void InsertSort(int* a, int n) {
  assert(a);
  int i = 0;
  for (i = 0; i < n - 1; i++) {
    int end = i;
    int x = a[end+1];
    while (end >= 0) {
      //要插入的数比顺序中的数小就准备挪位置
      if (a[end] > x) {
        a[end + 1] = a[end];
        end--;
      }
      else {
        //插入的数比顺序中的要大就跳出
        break;
      }
    }
    //跳出来两种情况
    //1.end == -1 的时候
    //2.break 的时候
    //把x给end前面一位
    a[end + 1] = x;
  }
}
// 希尔排序
void ShellSort(int* a, int n) {
  //分组
  int gap = n;
  //多次预排序（gap>1）+ 直接插入（gap == 1）
  while (gap>1){
    //gap /= 2;
    //除以三我们知道不一定会过1，所以我们+1让他有一个必过1的条件
    gap = gap / 3 + 1;
    //单组多躺
    int i = 0;
    for (i = 0; i < n - gap; i++) {
    int end = i;
    int x = a[end + gap];
    while (end >= 0) {
      if (a[end] > x) {
        a[end + gap] = a[end];
        //步长是gap
        end -= gap;
      }
      else {
        break;
      }
    }
    a[end + gap] = x;
  }
  } 
}
//数据交换
void Swap(int* pa, int* pb) {
  int tmp = *pa;
  *pa = *pb;
  *pb = tmp;
}
// 选择排序
void SelectSort(int* a, int n) {
  int begin = 0;
  int end = n - 1;
  while (begin < end){
    //单趟
    //最大数，最小数的下标
    int mini = begin;//这边假设是刚开始的下标
    int maxi = end;  //这边假设是末尾的下标
    int i = 0;
    for (i = begin; i <= end; i++) {
      if (a[i] < a[mini])
        mini = i;
      if (a[i] > a[maxi])
        maxi = i;
    }
    //最小的放前面
    Swap(&a[begin], &a[mini]);
    if (begin == maxi)
      //如果最大数就是begin位置的，那么交换的时候最大数连带着下标一起动
      maxi = mini;
    //最大的放后面
    Swap(&a[end], &a[maxi]);
    begin++;
    end--;
  }
}
//向下调整函数
void AdjustDown(int* a, int n, int parent)
{
  assert(a);
  //创建一个孩子变量，有两个孩子就在这个上加1就行
  int child = parent * 2 + 1;
#if HEAP
  while (child < n)
  {
    //选大孩子
    if (child + 1 < n && a[child] < a[child + 1])
    {
      child++;
    }
    //大的孩子还大于父亲就交换
    if (a[child] > a[parent])
    {
      Swap(&a[child], &a[parent]);
      parent = child;
      child = parent * 2 + 1;
    }
    else
    {
      break;
    }
  }
#elif !HEAP
  while (child < n)
  {
    //选小孩子
    if (child + 1 < n && a[child] > a[child + 1])
    {
      child++;
    }
    //小的孩子还小于父亲就交换
    if (a[child] < a[parent])
    {
      Swap(&a[child], &a[parent]);
      parent = child;
      child = parent * 2 + 1;
    }
    else
    {
      break;
    }
  }
#endif // HEAP  
}
// 堆排序   我们之前讲过升序建大堆
void HeapSort(int* a, int n) {
  //建堆时间复杂度O(N)
  //建大堆
  int i = 0;
  for (i = (n - 1 - 1) / 2; i >= 0; i--) {
    AdjustDown(a, n, i);
  }
  int end = n - 1;
  //堆排序时间复杂度O(N*logN)
  while (end>0){
    //交换 把最大的放到后面
    Swap(&a[0], &a[end]);
    //在向下调整
    AdjustDown(a,end,0);
    end--;
  }
}

test.c

#define _CRT_SECURE_NO_WARNINGS 1
#include "Sort.h"
// 测试排序的性能对比
void TestOP()
{
  //设置随机起点
  srand(time(NULL));
  //将要创建的数组大小
  const int N = 1000000;
  int* a1 = (int*)malloc(sizeof(int) * N);
  int* a2 = (int*)malloc(sizeof(int) * N);
  int* a3 = (int*)malloc(sizeof(int) * N);
  int* a4 = (int*)malloc(sizeof(int) * N);
  for (int i = 0; i < N; ++i)
  {
    //保证两个数组是一样的
    a1[i] = rand();
    a2[i] = a1[i];
    a3[i] = a1[i];
    a4[i] = a1[i];
  }
  int begin1 = clock();//开始时间
  //InsertSort(a1, N);
  int end1 = clock();  //结束时间
  int begin2 = clock();
  ShellSort(a2, N);
  int end2 = clock();
  int begin3 = clock();
  //SelectSort(a3, N);
  int end3 = clock();
  int begin4 = clock();
  HeapSort(a4, N);
  int end4 = clock();
  printf("InsertSort:%d\n", end1 - begin1);//结束时间减去开始时间 
  printf("ShellSort:%d\n", end2 - begin2);
  printf("SelectSort:%d\n", end3 - begin3);
  printf("HeapSort:%d\n", end4 - begin4);
  free(a1);
  free(a2);
  free(a3);
  free(a4);
}
//测试插入排序
void TestInsertSort() {
  int a[] = { 1,5,3,7,0,9 };
  InsertSort(a, sizeof(a) / sizeof(a[0]));  
  PrintArray(a, sizeof(a) / sizeof(a[0]));
}
//测试希尔排序
void TestShellSort() {
  int a[] = { 9,1,2,5,7,4,8,6,3,5 };
  ShellSort(a, sizeof(a) / sizeof(a[0]));
  PrintArray(a, sizeof(a) / sizeof(a[0]));
}
//测试选择排序
void TestSelectSort() {
  int a[] = { 9,1,2,5,7,4,8,6,3,5 };
  SelectSort(a, sizeof(a) / sizeof(a[0]));
  PrintArray(a, sizeof(a) / sizeof(a[0]));
}
//测试堆排序
void TestHeapSort() {
  int a[] = { 9,1,2,5,7,4,8,6,3,5 };
  HeapSort(a, sizeof(a) / sizeof(a[0]));
  PrintArray(a, sizeof(a) / sizeof(a[0]));
}
int main(){
  //TestInsertSort();
  //TestShellSort();
  //TestSelectSort();
  //TestHeapSort();
  TestOP();
  return 0;
}

算法给小码农选择排序搬血，堆排序化灵

排序

常见的排序算法

常见排序算法的实现

选择排序最慢排序（最好理解）所以搬血

基本思想：

直接选择排序

数据交换剥离出来其他函数也会用到我明明是简洁之人为了一时的高级而忘记了朴素罪过罪过

选择排序

堆排序

向下调整函数

堆排序代码

测性能让你看看什么叫堆

1000大小数组一千

10000大小数组一万

100000大小数组十万

1000000大小数组一百万

10000000大小数组一千万我们不带选择，插入玩太拉跨了，我们看看希尔，堆在超大数据面前谁性能更优

性能函数图

代码

Sort.h

Sort.c

test.c

热门文章

最新文章

相关课程

相关电子书

相关实验场景

热门

活动广场

任务中心

开发者评测

高校计划

乘风者计划

训练营

阿里云MVP

话题

直播

下载

镜像站

技术资料

插件

算法给小码农选择排序搬血，堆排序化灵

排序

常见的排序算法

常见排序算法的实现

选择排序 最慢排序（最好理解）所以搬血

基本思想：

直接选择排序

数据交换 剥离出来其他函数也会用到 我明明是简洁之人为了一时的高级而忘记了朴素罪过罪过

选择排序

堆排序

向下调整函数

堆排序代码

测性能 让你看看什么叫堆

1000大小数组 一千

10000大小数组 一万

100000大小数组 十万

1000000大小数组 一百万

10000000大小数组 一千万 我们不带选择，插入玩太拉跨了，我们看看希尔，堆在超大数据面前谁性能更优

性能函数图

代码

Sort.h

Sort.c

test.c

热门文章

最新文章

相关课程

相关电子书

相关实验场景

选择排序最慢排序（最好理解）所以搬血

数据交换剥离出来其他函数也会用到我明明是简洁之人为了一时的高级而忘记了朴素罪过罪过

测性能让你看看什么叫堆

1000大小数组一千

10000大小数组一万

100000大小数组十万

1000000大小数组一百万

10000000大小数组一千万我们不带选择，插入玩太拉跨了，我们看看希尔，堆在超大数据面前谁性能更优