matlab学习笔记3(控制系统仿真)
1、典型二阶系统
,绘制出
,
分别为0.1、0.2、0.3、···、1.0和2.0时的单位阶跃响应。
clear
clc
Wn=0.6;
kesai=[0.1:0.1:1,2];
hold on
for k=kesai
num=Wn^2;
den=[1 2*k*Wn Wn^2];
step(num,den);
end
title('step response');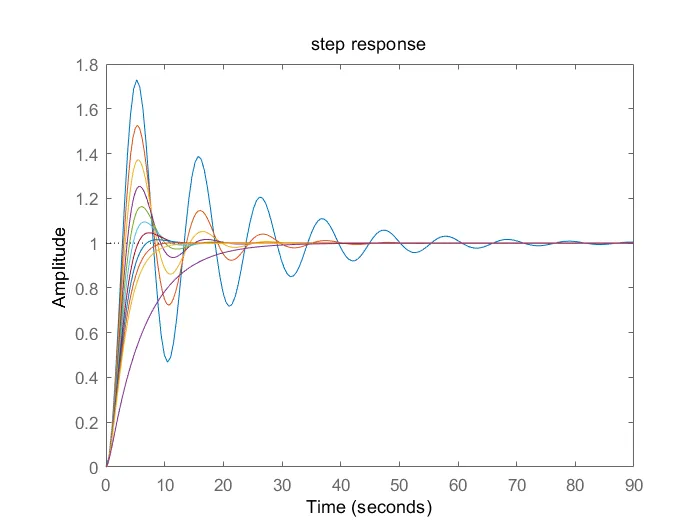
2、对1中的典型二阶系统,绘制出当
,
时的单位阶跃响应。
clear
clc
W=2:2:12;
kesai=0.7;
hold on
for wn=W
num=wn^2;
den=[1 2*kesai*wn wn^2];
step(num,den);
end
title('step response');
hold off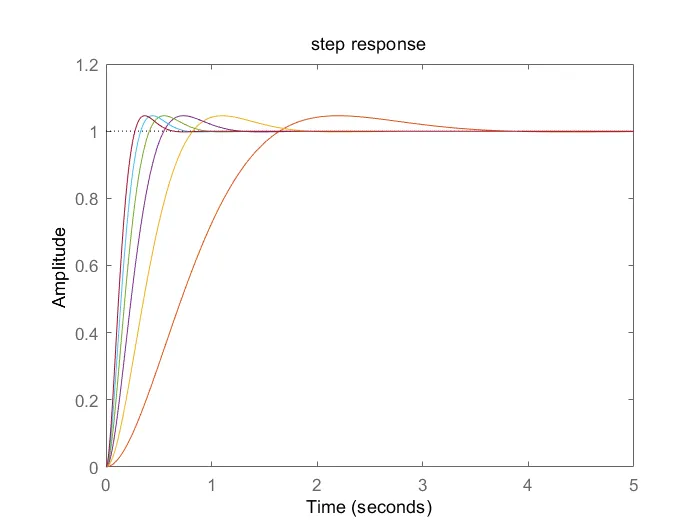
3、求三阶系统
的单位阶跃响应。
clear
clc
num=[5 25 30];
den=[1 6 10 8];
step(num,den);
title('step response');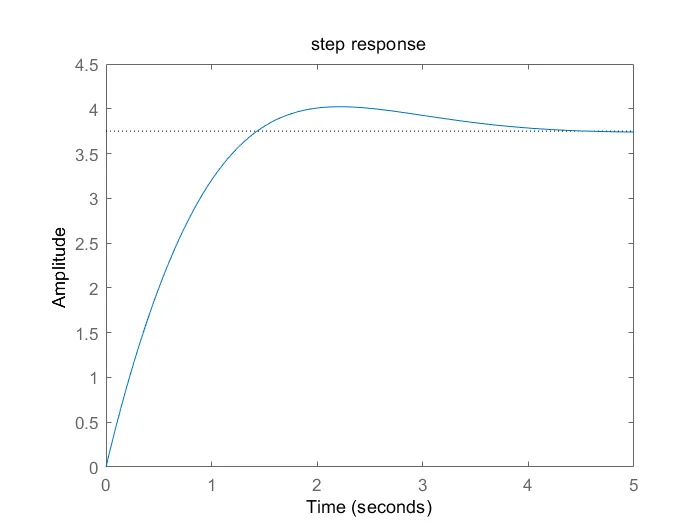
4、求典型二阶系统
,当
时的单位阶跃响应。
clear
clc
Wn=6;
kesai=0.7;
num=Wn^2;
den=[1 2*kesai*Wn Wn^2];
step(num,den);
title('step response');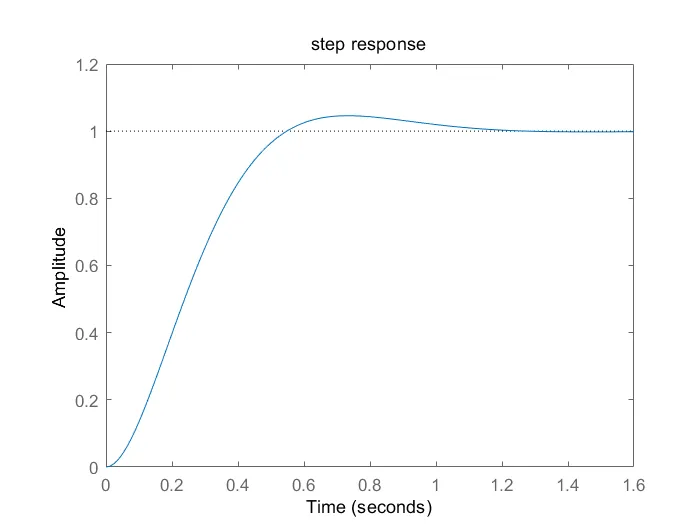
5、有高阶系统$\left\lbrace \begin{array}{l} \dot{x} =\left\lbrack \begin{array}{cccc} -1.6 & -0.9 & 0 & 0\\ 0.9 & 0 & 0 & 0\\ 0.4 & 0.5 & -5.0 & -2.45\\ 0 & 0 & 2.45 & 0 \end{array}\right\rbrack x+\left\lbrack \begin{array}{l}
1\
0\
1\
0
\end{array}\right\rbrack u\
y=\left\lbrack \begin{array}{llll} 1 & 1 & 1 & 1 \end{array}\right\rbrack x
\end{array}\right.
x_0 ={\left\lbrack 1\;,1,\;1,-1\right\rbrack }^T$。
a0=[-1.6,-0.9,0,0;0.9,0,0,0;0.4,0.5,-5.0,-2.45;0,0,2.45,0];
b0=[1 0 1 0]';
c0=[1 1 1 1];
d0=[0];
t=0.5; %采样周期
[a,b,c,d]=c2dm(a0,b0,c0,d0,t,'tustin');%连续系统离散化
subplot(2,2,1);
dstep(a,b,c,d);%离散系统的单位阶跃响应
title('discrete step response');
subplot(2,2,2);
dimpulse(a,b,c,d);%离散系统的单位冲激响应
title('discrete impulse response');
subplot(2,2,3);
x0=[1 1 1 -1]';%离散系统初始状态
dinitial(a,b,c,d,x0);
axis([0 6 -0.5 2.5]);
title('discrete initial response');
subplot(2,2,4);
[z,p,k]=ss2zp(a,b,c,d,1);%状态方程转化为零极点增益形式
zplane(z,p);
title('discrete ploe-zero map');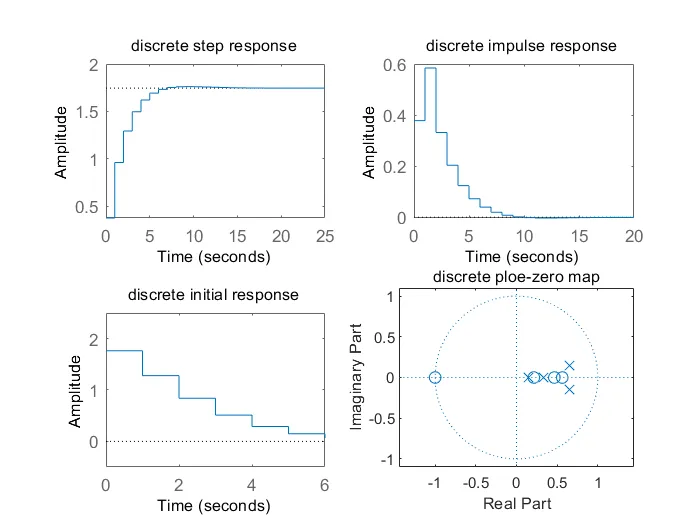
6、多输入多输出系统$\left\lbrace \begin{array}{l} \dot{x} =\left\lbrack \begin{array}{cccc} 2.25 & -5 & -1.25 & -0.5\\ 2.25 & -4.25 & -1.25 & -0.25\\ 0.25 & -0.5 & -1.25 & -1\\ 1.25 & -1.75 & -0.25 & -0.75 \end{array}\right\rbrack x+\left\lbrack \begin{array}{cc}
4 & 6\
2 & 4\
2 & 2\
0 & 2
\end{array}\right\rbrack u\
y=\left\lbrack \begin{array}{cccc} 0 & 0 & 0 & 1\\ 0 & 2 & 0 & 2 \end{array}\right\rbrack x
\end{array}\right.$,求单位阶跃响应和单位冲激响应。
clear
clc
a=[2.25 -5 -1.25 -0.5;
2.25 -4.25 -1.25 -0.25;
0.25 -0.5 -1.25 -1;
1.25 -1.75 -0.25 -0.75];
b=[4,6;2,4;2,2;0,2];
c=[0 0 0 1;0 2 0 2];
d=zeros(2,2);
subplot(1,2,1);
step(a,b,c,d);
title('step response');
subplot(1,2,2);
impulse(a,b,c,d);
title('impule response');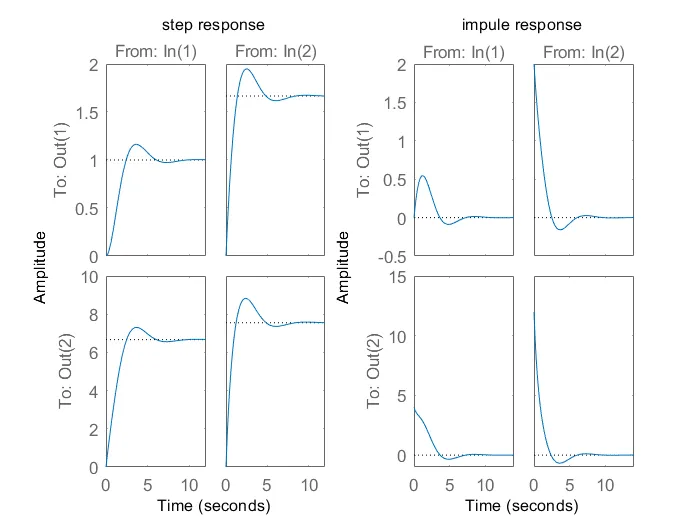
a0=[-1.6,-0.9,0,0;0.9,0,0,0;0.4,0.5,-5.0,-2.45;0,0,2.45,0];
b0=[1 0 1 0]';
c0=[1 1 1 1];
d0=[0];
t=0.5; %采样周期
[a,b,c,d]=c2dm(a0,b0,c0,d0,t,'tustin');%连续系统离散化
subplot(2,2,1);
dstep(a,b,c,d);%离散系统的单位阶跃响应
title('discrete step response');
subplot(2,2,2);
dimpulse(a,b,c,d);%离散系统的单位冲激响应
title('discrete impulse response');
subplot(2,2,3);
x0=[1 1 1 -1]';%离散系统初始状态
dinitial(a,b,c,d,x0);
axis([0 6 -0.5 2.5]);
title('discrete initial response');
subplot(2,2,4);
[z,p,k]=ss2zp(a,b,c,d,1);%状态方程转化为零极点增益形式
zplane(z,p);
title('discrete ploe-zero map');
matlab学习笔记4(控制系统仿真)
1、将5中的连续系统,以t=0.5 取样周期,采用双线性变换算法转换成离散系统,然后求出离散系统的单位阶跃响应、单位冲激响应及零输入响应,初始状态$x_0 ={\left\lbrack 1\;1\;1-1\right\rbrack }^T$ 。
clear
clc
a=[-1.6 -0.9 0 0;0.9 0 0 0;0.4 0.5 -5 -2.45;0 0 2.45 0];
b=[1,0,1,0]';
c=[1 1 1 1];
d=[0];
H=ss(a,b,c,d);
t=0.5;%采样周期
Gd=c2d(H,t,'tustin');%连续时间系统转化为离散时间系统
[ad,bd,cd,dd]=ssdata(Gd);
subplot(2,2,1);
dstep(ad,bd,cd,dd);
title('discrete step response');
subplot(2,2,2);
dimpulse(ad,bd,cd,dd);
title('discrete impulse response');
subplot(2,2,3);
x0=[1 1 1 -1]';
dinitial(ad,bd,cd,dd,x0);
axis([0 6 -0.5 2.5]);
title('discrete initial response');
subplot(2,2,4);
[z,p,k]=ss2zp(ad,bd,cd,dd,1);
zplane(z,p);
title('discrete ploe-zero map');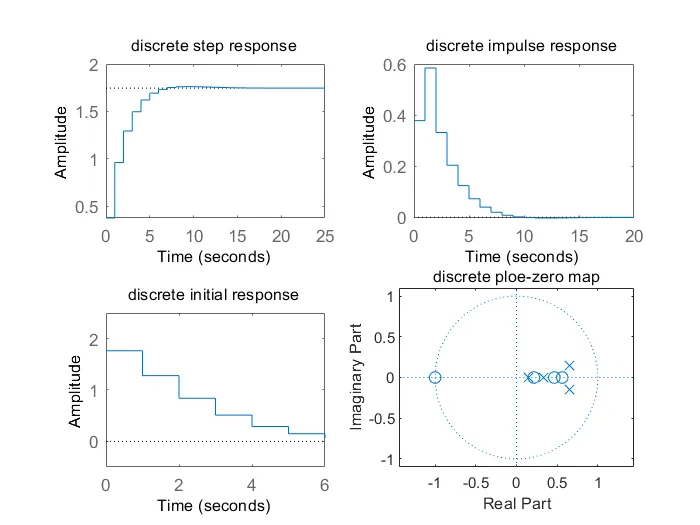
2、设开环传递函数$H(s)=\frac{k(3s+1)}{s(2s+1)}$,绘制出通过单位负反馈构成的闭环系统的根轨迹.
clear
clc
num=[3,1];
den=[2,1,0];
rlocus(num,den);
sgrid
title('根轨迹');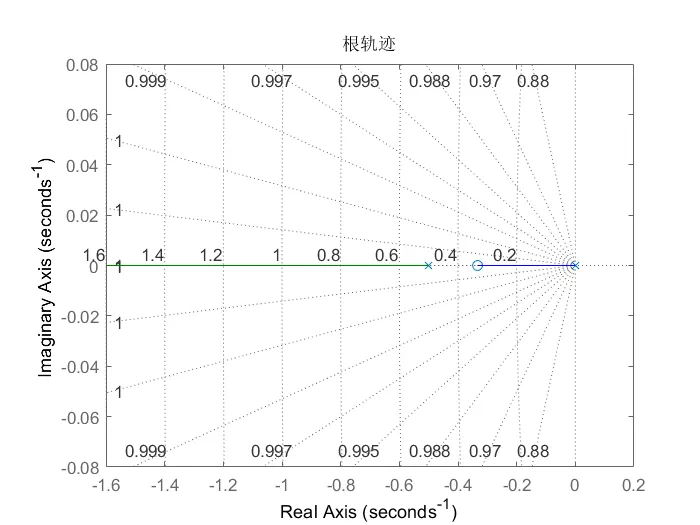
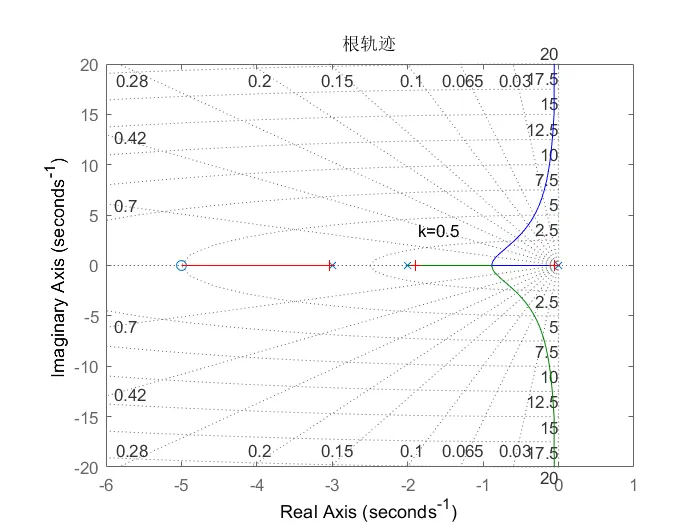
3、设开环系统$H\left(S\right)=\frac{k\left(S+5\right)}{S\left(S+2\right)\left(S+3\right)}$,绘制出闭环系统的根轨迹,并确定交点处的增益K。
clear
clc
num=[1 5];
den=[1 5 6 0];
rlocus(num,den);
sgrid
title('根轨迹');
[k,p]=rlocfind(num,den);Select a point in the graphics windowselected_point = - 1.9896 - 0.09931
10、已知开环传递函数为$H\left(S\right)=\frac{k}{S^4 +{16S}^3 +36S^2 +80S}$,绘制处闭环系统根轨迹,并分析其稳定性。
clearclcnum=[1];den=[1 16 36 80 0];rlocus(num,den);title('根轨迹');Select a point in the graphics window
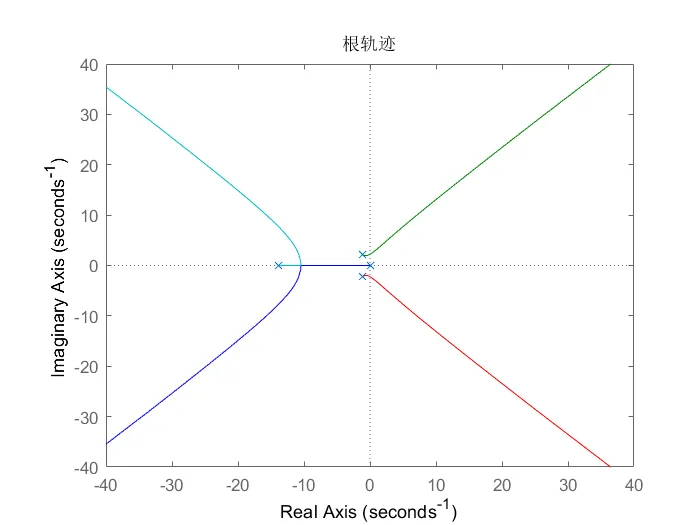
select_point = 0.0152 + 3.13651
figure(2);k1=55;num1=k1*num;den1=conv(den,den);G1=tf(num1,den1);[num_F1,den_F1]=feedback(G1,1,-1);%单位负反馈G1_0=tf(num_F1,den_F1);impulse(G1_0);title('impulse response(k=55)');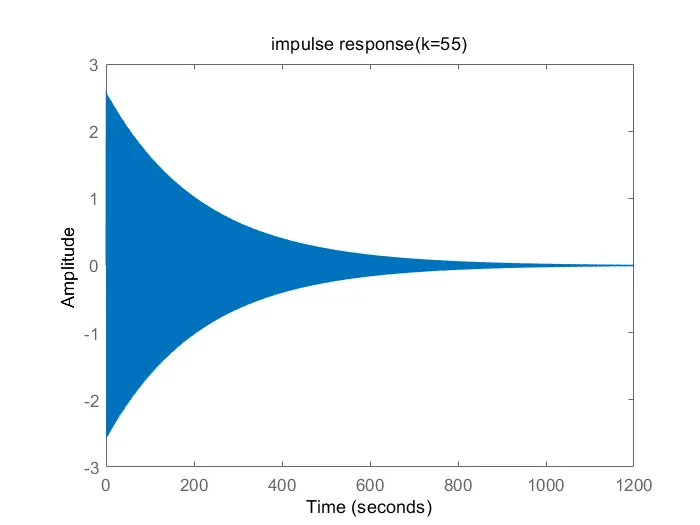
figure(3);
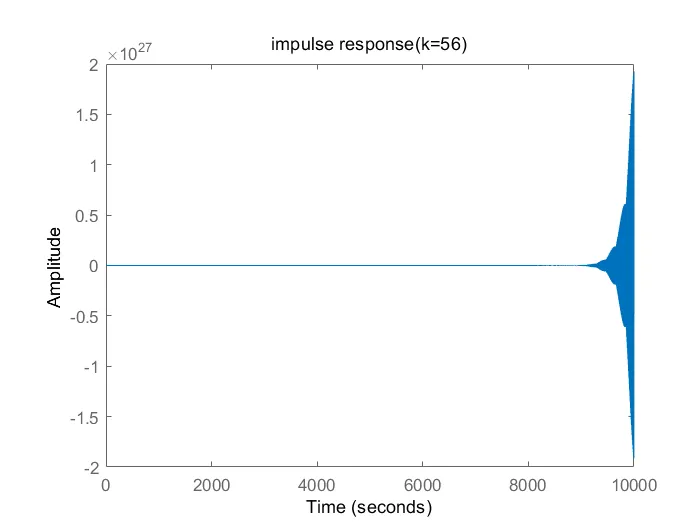
k2=56;
num2=k2*num;
den2=conv(den,den);
G2=tf(num2,den2);
[num_F2,den_F2]=feedback(G2,1,-1);
G2_0=tf(num_F2,den_F2);
impulse(G2_0);
title('impulse response(k=56)');