小菜上一节尝试绘制了一个简单的饼状图,今天尝试添加一点手势操作,可以随手指旋转饼状图;
ACEPieWidget
Gesture
小菜在之前绘制好的饼状图基础上添加一个简单的旋转手势操作;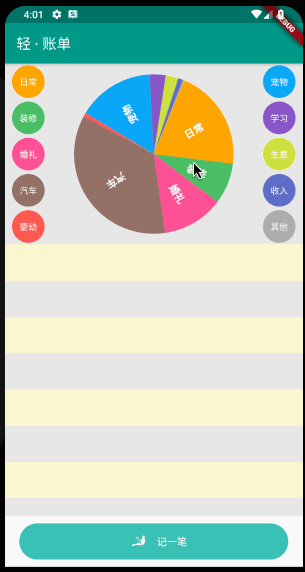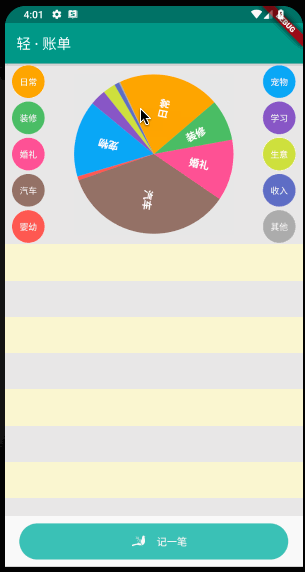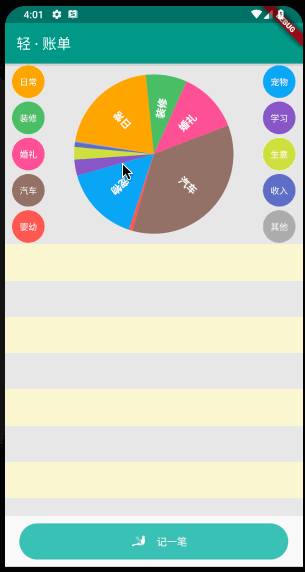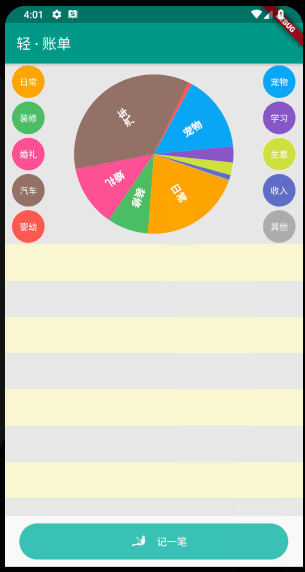
1. 手势范围
小菜习惯重写 PanGestureRecognizer 来对手势操作进行监听,也可以直接通过 Gesture 来直接处理;
return Container(
width: double.infinity,
height: double.infinity,
child: RawGestureDetector(
child: CustomPaint(
key: _key,
painter: PiePainter(widget.listData, this.rotateAngle)),
gestures: <Type, GestureRecognizerFactory>{
ACEPieGestureRecognizer:
GestureRecognizerFactoryWithHandlers<ACEPieGestureRecognizer>(
() => ACEPieGestureRecognizer(), (ACEPieGestureRecognizer gesture) {
gesture.onDown = (detail) {
};
gesture.onUpdate = (detail) {
};
gesture.onEnd = (detail) {
};
})
}));2. 计算旋转角度
小菜预计的想法是,通过 gesture.onUpdate 更新手势坐标,与初始坐标差来定位旋转角度;其中饼状图绘制是采用的笛卡尔坐标系,以左上角为坐标系原点;而居中的饼状图圆心是在整个组件所在的屏幕尺寸中心;
RenderBox box = _key.currentContext.findRenderObject();
Offset offset = box.localToGlobal(Offset.zero);
Offset _centerOffset = Offset(offset.dx + box.size.width * 0.5, offset.dy + box.size.height * 0.5); 小菜采用通用 RenderBox 的方式获取自定义 ACEPieWidget 所占屏幕尺寸并获取饼状图圆心坐标;
其中需要注意的是手势监听的 Offset details 获取坐标方式略有不同:detail.localPosition 获取的是当前组建内相对于左上角坐标原点的相对位置,而 detail.globalPosition 获取的是整个设备屏幕左上角坐标的实际位置,小菜刚开始通过 localPosition 方式获取,计算得出的角度受 Widget 所占位置及尺寸影响,差别较大,建议使用 globalPosition 方式;
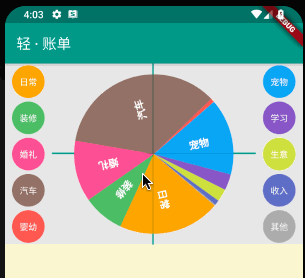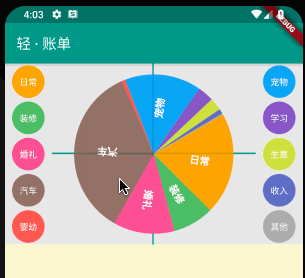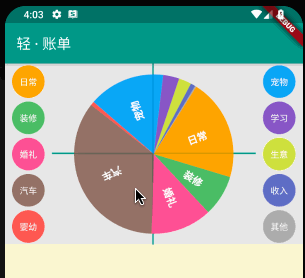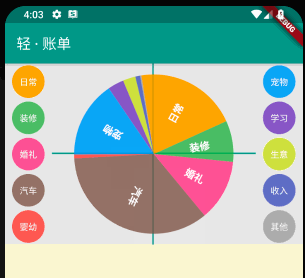
通过 gesture.onUpdate 更新后的坐标点与更新前的坐标点,再结合饼状图圆心坐标,三点确定一个三角形,通过余弦定律获取手势操作的夹角,从而重新绘制饼状图;
_rotateAngle() {
var _onDownLen = sqrt(pow(_startOffset.dx - _centerOffset.dx, 2) +
pow(_startOffset.dy - _centerOffset.dy, 2));
var _onUpdateLen = sqrt(pow(_updateOffset.dx - _centerOffset.dx, 2) +
pow(_updateOffset.dy - _centerOffset.dy, 2));
var _downToUpdateLen = sqrt(pow((_startOffset.dx - _updateOffset.dx), 2) +
pow((_startOffset.dy - _updateOffset.dy), 2));
var _cosAngle = (_onDownLen * _onDownLen + _onUpdateLen * _onUpdateLen -
_downToUpdateLen * _downToUpdateLen) / (2 * _onDownLen * _onUpdateLen);
rotateAngle += acos(_cosAngle);
setState(() {});
}
3. 旋转方向
小菜通过上述方式获取三角形角度后发现旋转的方向只能是顺时针旋转,反向的逆时针手势缺未生效;其原因是通过余弦定律转换的角度都为正数,需要通过向量方式进行方向正负的判断;于是小菜更换了另一种方式,以饼状图圆心为坐标轴原点,水平向右设置一个单位向量,再通过前后手势变更的坐标进行计算两个角度,相差即是夹角;
_rotateAngle() {
if (_startOffset.dy < _centerOffset.dy) {
gestureDirection = -1;
} else {
gestureDirection = 1;
}
var _updateAngle = gestureDirection *
_angle(_updateOffset, Offset(_centerOffset.dx + 100, _centerOffset.dy), _centerOffset);
if (_updateOffset.dy < _centerOffset.dy) {
gestureDirection = -1;
} else {
gestureDirection = 1;
}
var _startAngle = gestureDirection *
_angle(_startOffset, Offset(_centerOffset.dx + 100, _centerOffset.dy), _centerOffset);
return (_updateAngle - _startAngle);
}
_angle(_aPoint, _bPoint, _oPoint) {
var _oALen = sqrt(pow(_aPoint.dx - _oPoint.dx, 2) + pow(_aPoint.dy - _oPoint.dy, 2));
var _oBLen = sqrt(pow(_bPoint.dx - _oPoint.dx, 2) + pow(_bPoint.dy - _oPoint.dy, 2));
var _aBLen = sqrt(pow(_aPoint.dx - _bPoint.dx, 2) + pow(_aPoint.dy - _bPoint.dy, 2));
var _cosAngle = (pow(_oALen, 2) + pow(_oBLen, 2) - pow(_aBLen, 2)) /
(2 * _oALen * _oBLen);
return acos(_cosAngle);
}其中在计算的时候用到一些基本的数学函数公式,之后小菜会简单介绍一下 dart:math 函数库;计算所得的角度加在饼状图遍历绘制的扇形图角度中即可;其中注意在文字绘制时也要注意旋转坐标系角度;
if (_listData != null) {
for (int i = 0; i < _listData.length; i++) {
startAngle += sweepAngle;
sweepAngle = _listData[i].values.first * 2 * pi / _sum;
canvas.drawArc(_circle, startAngle + _rotateAngle, sweepAngle, true,
_paint..color = _subPaint(_listData[i].keys.first));
if (sweepAngle >= pi / 6) {
canvas.translate(size.width * 0.5, size.height * 0.5);
canvas.rotate(startAngle + sweepAngle * 0.5 + _rotateAngle);
Paragraph paragraph = (_pb..addText(_subName)).build()..layout(_paragraph);
canvas.drawParagraph(paragraph, Offset(50.0, 0.0 - paragraph.height * 0.5));
canvas.rotate(-startAngle - sweepAngle * 0.5 - _rotateAngle);
canvas.translate(-size.width * 0.5, -size.height * 0.5);
}
}
}
dart:math
小菜在绘制饼状图过程中需要使用三角函数等进行偏移量绘制,此时需要一些基础的数学计算;而 Dart 也有简单的 dart:math 库,主要用来数学常数和函数使用,以及随机数生成器等;
1. 常量数据
dart:math 提供了我们日常用的自然数底数 e、对数 ln 以及圆周率 pi 等,精确了很多位,避免我们自己定义;
// 自然对数的底数 e
'e -> $e';
// 以 e 为底 10 的对数
'ln10 -> $ln10';
// 以 e 为底 2 的对数
'ln2 -> $ln2';
// 以 2 为底 e 的对数
'log2e -> $log2e';
// 以 10 为底 e 的对数
'log10e -> $log10e';
// 圆周率
'pi -> $pi';
// 2 的平方根
'sqrt2 -> $sqrt2';
// 1/2 的平方根
'sqrt2 -> $sqrt2';2. 倍数/指数函数
dart:math 提供了平方根,求幂,指数函数等便利的函数方法;
// 平方根
double sqrt(num x);
// 自然指数 e 的 x 次幂
double exp(num x);
// 自然数 x 的对数
double log(num x);
// 最小值比较
T min<T extends num>(T a, T b);
// 最大值比较
T max<T extends num>(T a, T b);
// x 的 y 次幂
num pow(num x, num exponent);3. 三角函数
对于三角函数,提供了弧度转为角度的正弦/余弦/正切函数,同样提供了由角度值转为弧度值转换方法,需要注意例如负数、0、无穷数、无理数等特殊场景;
// 正弦函数
double sin(num radians);
// 余弦函数
double cos(num radians);
// 正切函数
double tan(num radians);
// 弧度转为正弦值
double asin(num x);
// 弧度转为余弦值
double acos(num x);
// 弧度转为正切值
double atan(num x);
来源: 阿策小和尚