Java系统提供的Arrays.sort函数。对于基础类型,底层使用快速排序。对于非基础类型,底层使用归并排序。请问是为什么?
答:这是考虑到排序算法的稳定性。对于基础类型,相同值是无差别的,排序前后相同值的相对位置并不重要,所以选择更为高效的快速排序,尽管它是不稳定的排序算法;而对于非基础类型,排序前后相等实例的相对位置不宜改变,所以选择稳定的归并排序。
在JDK的源码中也使用了归并排序,可见归并排序的重要性。我们一起来看看归并排序吧
归并排序
复杂度:
时间复杂度为:O(nlog₂n) 这是该算法中最好、最坏和平均的时间性能。
空间复杂度:O(n)
Java实现
图解
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。

image.png
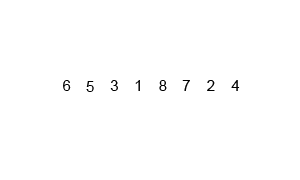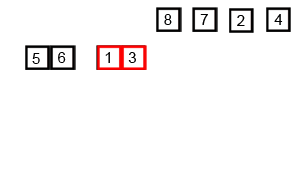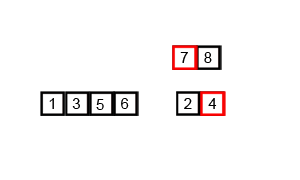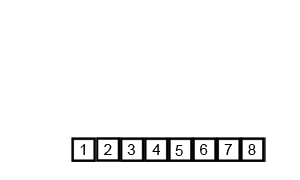
image
代码
在比较代码中,我们需要定义三个下标。
分别指向当前数组要比较的左部分下标
分别指向当前数组要比较的右部分下标
当前数组要填充的元素
注意数组的边界。
@Slf4j
public class MergeSort {
public static void main(String[] args) {
//可随机生成数组
int[] a = {6,202,100,301,38,8,1};
mergeInternal(a,0,a.length - 1);
for (int i = 0; i < a.length; i++) {
System.out.println(a[i]);
}
}
/**
* 对数组进行归并
*
* @param arr
* @param l,数组左边下标
* @param r 数组右边下标
*/
public static void mergeInternal(int[] arr,int l,int r){
if (l >= r){
//这里可以进行优化,在最后要比较的数组范围较小时候进行插入排序。
return;
}
//两个下标的中间元素
int mid = (l + r) / 2;
//递归操作
mergeInternal(arr, l, mid);
mergeInternal(arr,mid + 1, r);
// 当mid < mid+1时,代表已经排序过了
if (arr[mid] < arr[mid + 1]){
return;
}
merge(arr,l,mid,r);
}
/**
*
* @param arr
* @param l //左下标
* @param mid //中间位置
* @param r 右下标
*/
private static void merge(int[] arr,int l,int mid,int r) {
//新建临时数组
int[] temp = new int[(r - l)+1];
for (int i = 0; i < temp.length; i++) {
temp[i] = arr[ l + i ];
}
int i = l;
int j = mid + 1;
for (int k = l; k <= r; k++) {
// 当左下标拍完序之后,进行右下标的排序
if (i > mid){
arr[ k ] = temp[j - l];
j++;
// 有下标全部排序完成
}else if (j > r){
arr[ k ] = temp[i - l];
i++;
// 进行比较
}else if (temp[i - l ] < temp[j - l]){
arr[k] = temp[i - l];
i++;
}else if (temp[i - l] >= temp[j - l]){
arr[k] = temp[j - l];
j++;
}
}
}
}
AI 代码解读
优化部分
- 归并排序在进行数组排序之前,判断是否已经左右有序了,比较数组的mid下标与mid+1下标
- 在最后数据量分到较小的时候,进行插入排序。
最后
个人觉得归并排序是一个很重要的知识,在数据量足够大的时候进行排序还是要掌握一种高效稳定的排序方法。


