前言:常见的数据结构都有指针和数组两种实现方式,这篇先介绍指针实现,而数组实现在后续文章里会讲到。
(长文预警!)
说完了一般的树,我们再来看看二叉树,这是一种很典型的树,它的所有节点度数都不超过2,最多只有两个孩子。这是一种特例,但是后面我们会看到在保证有序性和有根性之后,它却足以描述所有的树。每个节点的出度最多为2,在之前对所有节点按照深度划分的等价类,从规模上看就构成了一个公比为2的等比数列,相应地,深度为k(第k层)的节点,最多有2^k个。那么对于含n个节点、高度为h的二叉树中(这里再多说一句,高度指的是:除了根节点,下面有几层高度就是几,回想一下,空树高度是-1,一个根节点高度为0。),满足这样一个条件:
h<n<2^h+1。
这个性质很好证明。对于上界的情况,树的每一层都是满的,所以从根到第n层累加,总数=1+2+4+…+2^n=2^(n+1)-1,也就是右半部分。而下界情况,根据定义每层至少有一个节点,所以一共h+1个,这种情况下,树就退化为一条单链。
具体来说一下上界的情况,在这个时候节点个数n=2^h-1,是一颗满树,那每一层(每一个等价类)都会到达饱和状态。它的横向上的宽度与在纵向上的高度是呈指数关系的——h=log(W),高度会增长的很慢。

相关实现
讨论了二叉树的基本信息后,就该进入正题了,Talk is cheap,show me the code。现在来谈谈怎么在计算机中实现一棵二叉树。谈一个东西的实现不能脱离实际背景,不然就成了空中楼阁,二叉树也有很多种,比如最大堆,最小堆,优先队列,搜索树,这里给出一个其中一个二叉树的具体例子。首先需要知道的是,二叉树的一个重要应用是他们在查找(搜索)中的使用,那为什么查找往往要依靠树形结构呢?这是很自然的一个问题,前面的文章中我们说过,树结构对静态和动态操作的支持都是十分迅速的,因此是这种高效性使得树结构成为了搜索的“天选之人”。这也告诉我们,如果自身很强,那么遇到机会时才有可能把握住,机会是留给有准备的人(突然鸡汤2333)。
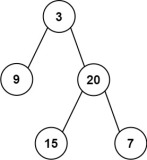
假设树中的每个节点内部存了一个值,任何复杂的值都可以,不过这里为了简单起见,让它们都是int型,同时假设他们是互异的,以后我们再处理有重复值的情形。我们要进行一些操作的前提是:知道规则,有了规则,操作的步骤就一目了然了,这是老师在课上反复强调的。那搜索树的规则就是——对于每个节点X(作为根),左子树中存的所有值都小于X存的值;右子树的所有值都大于X的值。也就是从小到大依次是左-根-右,就像这样:

这个性质要引起注意,这意味着树中的所有元素可以用统一的方式排序。为什么要这样说?因为树是递归构造的,其中每一棵子树中都满足这个性质,那我们的排序过程就可以逐步分解到最小的子树中,每个被分解的部分和原来的总体都是“性质相同的子问题”这样一种关系,所以可以用统一的方法,从最小的子问题推而广之,直至解决整个问题。
现在具体说说怎么实现他们,由于树是递归定义的,所以通常递归地编写操作函数,前面说了,二叉树的平均深度是多少来着?忘的话往上翻翻。由于平均深度增长地很慢,所以我们不必担心栈空间被用尽(emmm这怎么突然提到栈了,忘了的话去前面讲栈的文章里翻翻)。先给出一般性的结点声明
1 struct BinNode;
2 typedef struct BinNode *Position; //只需要拿到某个单结点时用它表示
3 typedef struct BinNode *SearchTree; //对整棵树操作时,用它表示返回类型
4
5 struct BinNode{
6 int Value;
7 SearchTree Left,Right;
8 };
这里又遇到和链表那里一样,用两个typedef替换同一个类型的情况了,稍后我们会看到如此逻辑分层的优势,它便于我们在大脑中构建一个清晰的搜索树ADT模型。现在只要知道他们表示的都是一个指向二叉树节点的指针就好了,只是所指示的侧重有细微的不同。按照惯例,先说初始化的操作,然后说查找元素,最后就是重头戏——插入和删除了。每种结构都按这个顺序来讲解看似单调乏味,但这的确是我们从0搭建一个结构的必由之路,从简到繁,自下而上这也符合人类的认知规律。
1 SearchTree MakeEmpty(SearchTree T){
2 if (T){
3 MakeEmpty(T->Left);
4 MakeEmpty(T->Right);
5 free(T);
6 }
7 return NULL;
8 }
给这个函数输入一个节点作为根,然后在它不为空的情况下,逐层递归地销毁它以下的所有子树。注意到了吧,这里用的是“SearchTree”来标识,因为置空后要返回的是一个根节点,实际上从整体理解,是以返回值为根的一整棵树(当然这里是空树)。
再说查找,它要返回的是一个指针,指向我们所查的值所在的结点(既然只返回一个单一结点指针,自然用Position做返回类型更清晰),没有的话就NULL。树的结构使得这种操作很简单,我们先分析一下大体策略:如果T是NULL,也就是走到某一个叶子结点仍然没有找到,那就返回NULL;如果T中存的值是要查找的X,那么返回T的地址;如果既没找到,但也没走到末尾(叶结点)时,就按照X和根节点的大小关系来逐层递归左或右子树:如果比根小,左边,否则右边,这就很类似二分查找的思想。
1 Position Find(int X,SearchTree T){
2 if(T == NULL) return NULL; //如果走到叶子还没找到,返回空
3 if (X < T->Value) return Find(X, T->Left); //如果给定值比根小,往左边找
4 else if(X > T->Value) return Find(X , T->Right);//比根大就往右找
5 else return T; //这种情况就是某时X==T->Value,正好命中的情况
6 }
接着来说两种Find的具体情况,分别是找最小最大值,这种递归写法是很自然的,以至于深受喜爱,不过递归调用过多的话会占用大量资源,这是一个弊端,所以迭代和递归两种方法都要熟稔于心。因此,我们用两种方法编写,FindMin(递归)和FindMax(迭代)。
1 Position FindMin(SearchTree T){
2 if(T == NULL) return NULL; //同上
3 else if (T->Left==NULL) return T; //左子树空,意味着没有比它更小的值了,直接返回地址
4 else return FindMin(T->Left); //如果上面两个情况都不符合,接着往左找
5 }
1 Position FindMax(SearchTree T) {
2 if (T!=NULL) //没有走到叶结点时寻找
3 while (T->Right!=NULL) //右边还有子树时一直往右走
4 T=T->Right;
5 return T; //这个return包含了两种情形,如果传入的是叶子,自动返回NULL,如果找到最右边了,返回对应地址
6 }
同理,查找最小值的如果用迭代来写,就是完全对称的。
1 SearchTree FindMinByLoop(SearchTree T) {
2 if(T)
3 while (T->Left)
4 T=T->Left;
5 return T;
6 }
这里要注意时如何处理空树这种退化情形的,一定要小心。
接着就是两大重头戏——插入和删除,我们慢慢讨论,对于插入一个数X来讲,从概念上很好理解:先用find查一下,看是不是已经存在,有的话就不用做什么了(或者做一些修改)。如果没有,就把X插到遍历路径的末尾。
比如对于这样一棵树

我们要插入66这个数,那么就应该按下面这个路径放置。

1 SearchTree Insert(SearchTree T,int X) {
2 if(!T){ //这是应对初始情况,空树
3 T=(SearchTree)malloc(sizeof(struct BinNode));
4 T->Value=X;
5 T->Left=T->Right=NULL; //底部封口
6 }
7 //在一棵现成的树里插入,二分查找
8 else if (X < T->Value) T->Left=Insert(T->Left, X);
9 else if (X > T->Value) T->Right=Insert(T->Right, X);
10 //X==T->Value的情况什么也不用做
11 return T;
12 }
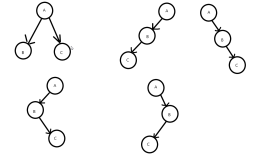
而正如许多数据结构一样,最困难的是删除,因为这会涉及到好多种情况,我们都需要将其考虑在内。
- 节点是一片叶子
- 节点有一个儿子
- 节点有两个儿子
分类讨论,1.叶子的话就直接删除。
2.只有一个儿子的话,就可以在它的父节点调整指针时绕过该节点后被删除。

这棵树中,删除4

从父节点直接绕过去,bypass

而有两个儿子的话情况就复杂了,一般来说是用它右子树下最小的数据来代替该节点数据并递归删除。因为右子树下面最小的节点不可能有左儿子,所以第二次delete就更容易了。
//好像插入不了视频……所以请点击 这里查看删除演示。如果你们知道怎么弄,请在评论里告诉我,我试过插入源代码,还是不行Orz
总结起来就是:
search for v
if v is a leaf
delete leaf v
else if v has 1 child
bypass v
else replace v with successor
代码如下
1 SearchTree Delete(int X,SearchTree T) {
2 Position TempCell;
3 if (T==NULL)
4 printf("Element not found\n");
5 //search for Value
6
7 else if(X<T->Value) T->Left=Delete(X, T->Left);
8 else if(X>T->Value) T->Right=Delete(X, T->Right);
9 //找到给定的X了,开始分类讨论
10 else if(T->Left && T->Right){ //有两个儿子的情况
11 TempCell=FindMin(T->Right); //找到右子树下最小的数据
12 T->Value=TempCell->Value; //Replace
13 T->Right=Delete(T->Value, T->Right); //递归删除
14 }
15 else{ //1个儿子or叶子的情况,可以统一起来,操作逻辑是一致的
16 TempCell=T;
17 if (T->Left==NULL) T=T->Right; //只有右孩子,就把父节点直接连到右边
18 else if (T->Right==NULL) T=T->Left; //只有左孩子,就把父节点直接连到左边
19 free(TempCell);
20 }
21 return T;
22 }
这里0 or 1 children的情况在实现的时候统一写了,不用再讨论他们的差别了。因为即使是叶子,进入分支后也就相当于原来的T=T->Right效果变成了T=NULL,同样达到了目的。如果我们一开始来写,可能会多写一条分支判断是否为叶子,这样代码就显得冗余了,也正因此我们需要慢慢品味上面这种写法的精妙之处。
小零件我们都写好了,下面就需要把他们粘合起来,形成一个有机的系统了。怎么粘合才能让他们各个部分有序而协调地运转呢?先走谁后走谁的问题就涉及到了遍历规则了,所以下面我们来讨论树的遍历。
遍历
树的主要遍历方式有四种:Pre/In/Post order和Level order,前者对应着深搜,后者对应广搜。层序遍历是按照离根节点的距离由远及近地访问。与层序不同,其他三种都是根据对根节点的访问次序来划分的。如果是先于左右子树,那就是Preorder,如果是介于左右子树之间,就是Inorder,如果是位于左右子树遍历之后,就是Postorder。

通过这张图我们来对比记忆,下面详细说明每种方法。

这是层序遍历,结果是ADBFHCEG。它的思想是用一个队列来维护,对于每个节点进行如下操作:
1.将这个节点入队
2.打印后出队
3.接着把该节点所有孩子按顺序入队
然后对所有孩子重复第2,3步,很显然,这是用递归轻松解决的。

这是先序遍历,而这条红色的线有一个名字叫Euler tour,preorder的结果就是GDBFAHEIC。
postorder的话,就是FBDEIHCAG,inorder的结果是:DFBGEHIAC。
1 void PreOrder(SearchTree T) {
2 if(T){ //如果这颗子树非空,就打印,否则把控制权还给上级
3 printf("%d ",T->Value);
4 PreOrder(T->Left);
5 PreOrder(T->Right);
6 }
7 }
中序的情况类似
1 void InOrder(SearchTree T){
2 if(T){
3 InOrder(T->Left);
4 printf("%d ",T->Value);
5 InOrder(T->Right);
6 }
7 }
后序同理,只是打印顺序略有区别,这里不再赘述。不过我要说的是,后序有一个妙用,就是计算树的高度,当然其他方式也可以,不过后序最符合人的思维习惯。
1 int Height(SearchTree T){
2 //下面这两句都是根据定义得出的
3 if(!T) return -1;
4 else return 1+max(Height(T->Left), Height(T->Right));
5 }
而层序遍历就稍微复杂一些了,因为它涉及到如何判断“某个节点是否被访问”以及“如何按照远近关系来行进”,这就需要我们为其指定一个优先级,故需要队列。
1 void LevelOrder(SearchTree r) {
2 SearchTree current=r; //为了不修改根节点,新建一个指针作为光标
3 queue<SearchTree> q;
4 q.push(current); //把当前(根)节点入队
5 //以下是广搜的核心
6 while (!q.empty()) { //队列非空时进行遍历
7 current=q.front();
8 printf("%d ",current->Value);
9 q.pop(); //打印完则出队
10 if (current->Left) //依次查看当前节点是否有后继,有的话重复上述入队过程,left,right or both
11 q.push(current->Left);
12 if (current->Right)
13 q.push(current->Right);
14 }
15 }
最后看一个具体的总实现,给出演示程序。
以这个为例,插入17,删除72

就分别变成

和

1 //出于布局合理的考虑,把主函数放在中间。 2 #include <cstdio> 3 #include <cstdlib> 4 #include <ctime> 5 #include <queue> 6 using namespace std; 7 8 struct BinNode; 9 typedef struct BinNode *SearchTree; 10 typedef struct BinNode *Position; 11 struct BinNode{ 12 int Value; 13 SearchTree Left,Right; 14 }; 15 16 SearchTree root=NULL; 17 18 // Function signature 19 SearchTree Insert(SearchTree T,int X); 20 SearchTree Delete(int X,SearchTree T); 21 int Height(SearchTree T); 22 void PreOrder(SearchTree T); 23 void InOrder(SearchTree T); 24 void LevelOrder(SearchTree T); 25 void DisplayInfo(SearchTree t); 26 Position FindMax(SearchTree T); 27 Position FindMix(SearchTree T); 28 //Entrance 29 int main(){ 30 int n; 31 printf("Could you tell me what the tree looks like?(0 to complete)\n"); 32 while (scanf("%d",&n) && n) 33 root=Insert(root, n); 34 printf("\n"); 35 DisplayInfo(root); 36 printf("Which guys will be pushed?\n"); scanf("%d",&n); 37 root=Insert(root, n); DisplayInfo(root); 38 printf("Which value do you desire to remove?\n"); scanf("%d",&n); 39 root=Delete(n, root); 40 DisplayInfo(root); printf("\n"); 41 } 42 43 //接口内部一览 44 SearchTree MakeEmpty(SearchTree T){ 45 if (T){ 46 MakeEmpty(T->Left); 47 MakeEmpty(T->Right); 48 free(T); 49 } 50 return NULL; 51 } 52 53 Position Find(int X,SearchTree T){ 54 if(T == NULL) return NULL; //如果走到叶子还没找到,返回空 55 if (X < T->Value) return Find(X, T->Left); //如果给定值比根小,往左边找 56 else if(X > T->Value) return Find(X , T->Right);//比根大就往右找 57 else return T; //这种情况就是某时X==T->Value,正好命中的情况 58 } 59 60 Position FindMin(SearchTree T){ 61 if(T == NULL) return NULL; //同上 62 else if (T->Left==NULL) return T; //左子树空,意味着没有比它更小的值了,直接返回地址 63 else return FindMin(T->Left); //如果上面两个情况都不符合,接着往左找 64 } 65 66 void DisplayInfo(SearchTree t){ 67 printf("\nCurrently\nPre-order is :"); 68 PreOrder(t); printf("\n"); 69 printf("In-order is :"); 70 InOrder(t); printf("\n"); 71 printf("Level-order is :"); 72 LevelOrder(t); printf("\n"); 73 printf("Height is %d\n",Height(root)); 74 printf("The min is: %d\n",FindMin(root)->Value); 75 printf("The max is: %d\n",FindMax(root)->Value); 76 } 77 78 int Height(SearchTree T){ 79 //这两句都是根据定义得出的 80 if(!T) return -1; 81 else return 1+max(Height(T->Left), Height(T->Right)); 82 } 83 SearchTree FindMinByLoop(SearchTree T) { 84 if(T) 85 while (T->Left) 86 T=T->Left; 87 return T; 88 } 89 90 Position FindMax(SearchTree T) { 91 if (T!=NULL) //没有走到叶结点时寻找 92 while (T->Right!=NULL) //右边还有子树时一直往右走 93 T=T->Right; 94 return T; //这个return包含了两种情形,如果传入的是叶子,自动返回NULL,如果找到最右边了,返回对应地址 95 } 96 97 SearchTree Insert(SearchTree T,int X) { 98 if(!T){ //这是应对初始情况,空树 99 T=(SearchTree)malloc(sizeof(struct BinNode)); 100 T->Value=X; 101 T->Left=T->Right=NULL; //底部封口 102 } 103 //在一棵现成的树里插入,二分查找 104 else if (X < T->Value) T->Left=Insert(T->Left, X); 105 else if (X > T->Value) T->Right=Insert(T->Right, X); 106 //X==T->Value的情况什么也不用做 107 return T; 108 } 109 SearchTree Delete(int X,SearchTree T) { 110 Position TempCell; 111 if (T==NULL) 112 printf("Element not found\n"); 113 //search for Value 114 115 else if(X<T->Value) T->Left=Delete(X, T->Left); 116 else if(X>T->Value) T->Right=Delete(X, T->Right); 117 //找到给定的X了,开始分类讨论 118 else if(T->Left && T->Right){ //有两个儿子的情况 119 TempCell=FindMin(T->Right); //找到右子树下最小的数据 120 T->Value=TempCell->Value; //Replace 121 T->Right=Delete(T->Value, T->Right); //递归删除 122 } 123 else{ //1个儿子or叶子的情况,可以统一起来,操作逻辑是一致的 124 TempCell=T; 125 if (T->Left==NULL) //只有右孩子,就把父节点直接连到右边 126 T=T->Right; 127 else if (T->Right==NULL){ //只有左孩子,就把父节点直接连到左边 128 T=T->Left; 129 } 130 free(TempCell); 131 } 132 return T; 133 } 134 135 136 void PreOrder(SearchTree T) { 137 if(T){ //如果这颗子树非空,就打印,否则把控制权还给上级 138 printf("%d ",T->Value); 139 PreOrder(T->Left); 140 PreOrder(T->Right); 141 } 142 } 143 void InOrder(SearchTree T){ 144 if(T){ 145 InOrder(T->Left); 146 printf("%d ",T->Value); 147 InOrder(T->Right); 148 } 149 } 150 151 void LevelOrder(SearchTree r) { 152 SearchTree current=r; //为了不修改根节点,新建一个指针作为光标 153 queue<SearchTree> q; 154 q.push(current); //把当前(根)节点入队 155 //以下是广搜的核心 156 while (!q.empty()) { //队列非空时进行遍历 157 current=q.front(); 158 printf("%d ",current->Value); 159 q.pop(); //打印完则出队 160 if (current->Left) //依次查看当前节点是否有后继,有的话重复上述入队过程,left,right or both 161 q.push(current->Left); 162 if (current->Right) 163 q.push(current->Right); 164 } 165 }