来考虑这样一种情况,先来看代码:
|
1
2
3
4
5
6
7
8
|
public
static
void
main(String[] args){
System.out.println(
0.4
+
0.8
);
// = 1.2 ?
System.out.println(
2
-
1.1
);
// = 0.9 ?
System.out.println(
0.2
*
3
);
// = 0.6 ?
System.out.println(
1.2
/
3
);
// = 0.4 ?
}
|
也许你会天真的认为,第一行打印 1.2,第二行打印 0.9,第三行打印 0.6,第四行打印 0.4,因为依据多年的数学惯性逻辑输出结果与预期的一致是很理所当然的事情嘛!
但是当程序跑完之后,输出的结果与预期的大有出入,来看下后台打印的结果:
|
1
2
3
4
|
1.2000000000000002
0.8999999999999999
0.6000000000000001
0.39999999999999997
|
结果看到这样的结果,是不是很让人郁闷呢?当然了,这些数据是我故意挑的,并不是所有涉及浮点数的运算操作都会算出这样预期之外的结果,但是一件很明了的事情就是,
当操作涉及浮点数运算的时候,我们一定要谨防这样的事情发生。
上面代码中,加也好,减也好,乘也好,除也好,它们都是属于 double 级别的运算,那为什么会打印输出这样的结果呢?原因是,并不是所有的浮点数都能够被精确的表示成一个
double 类型值,有些浮点数值不能够被精确的表示成 double 类型值,因此它会被表示成与它最接近的 double 类型的值。所以很遗憾,0.4 + 0.8 ≠ 1.2 。……
怎么来解决这个问题呢?在 java 中提供了一个 BigDecimal 类来执行精确小数的计算,BigDecimal 类提供了以下操作:算术、标度操作、舍入、比较、哈希算法和格式转换。
BigDecimal 类提供的方法:
加法:add
减法:subtract
乘法:multiply
除法:divide
…… ……
BigDecimal 类提供的更多的方法请自行查看 API,下面用 BigDecimal 类改写上面的代码实现:
|
1
2
3
4
5
6
7
8
|
public
static
void
main(String[] args){
System.out.println(
new
BigDecimal(
0.4
).add(
new
BigDecimal(
0.8
)));
// = 1.2 ?
System.out.println(
new
BigDecimal(
2
).subtract(
new
BigDecimal(
1.1
)));
// = 0.9 ?
System.out.println(
new
BigDecimal(
0.2
).multiply(
new
BigDecimal(
3
)));
// = 0.6 ?
System.out.println(
new
BigDecimal(
1.2
).divide(
new
BigDecimal(
3
)));
// = 0.4 ?
}
|
也许你正在查类 BigDecimal 的 API,API 上对类 BigDecimal 有一大串的文字说明,也许你还没来得及看完,但能够确定的是,类 BigDecimal 确实能够准确保证精确小数的执行,
那我上面代码的注释是不是忘记去掉了啊?不是。要是真这么干,那就大祸了。先来看一下后台的打印输出结果:
|
1
2
3
|
1.20000000000000006661338147750939242541790008544921875
0.899999999999999911182158029987476766109466552734375
0.60000000000000003330669073875469621270895004272460937
|
Exception in thread "main" java.lang.ArithmeticException: Non-terminating decimal expansion; no exact representable decimal result.
at java.math.BigDecimal.divide(BigDecimal.java:1603)
at example.BigDecimalApp.main(BigDecimalApp.java:20)
如果真这么玩了,你会看到结果更恶心了,这还不算,而且还抛了异常,这是为什么呢?别急,来看一下 API 上是怎么说的:
“
public BigDecimal(double val)
将 double 转换为 BigDecimal,后者是 double 的二进制浮点值准确的十进制表示形式。返回的 BigDecimal 的标度是使 (10scale × val) 为整数的最小值。
注:
1. 此构造方法的结果有一定的不可预知性。有人可能认为在 Java 中写入 new BigDecimal(0.1) 所创建的 BigDecimal 正好等于 0.1(非标度值 1,其标度为 1),但是它实际上等于
0.1000000000000000055511151231257827021181583404541015625。这是因为 0.1 无法准确地表示为 double (或者说对于该情况,不能表示为任何有限长度的二进制小数)
这样,传入 到构造方法的值不会正好等于 0.1(虽然表面上等于该值)。
2. 另一方面,String 构造方法是完全可预知的:写入 new BigDecimal("0.1") 将创建一个 BigDecimal,它正好 等于预期的 0.1。因此,比较而言,通常建议优先使用 String 构造方法
3. 当 double 必须用作 BigDecimal 的源时,请注意,此构造方法提供了一个准确转换;它不提供与以下操作相同的结果:先使用 Double.toString(double) 方法,
然后使用 BigDecimal(String) 构造方法,将 double 转换为 String。要获取该结果,请使用 static valueOf(double) 方法。
参数:
val - 要转换为 BigDecimal 的 double 值。
抛出:
NumberFormatException - 如果 val 为无穷大或 NaN。
”
以上文字摘自 API,API 上解释的很清楚了,这里就不多说了,API 建议优先使用 String 构造方法,那我们就来试一下呗:
|
1
2
3
4
5
6
7
8
|
public
static
void
main(String[] args){
System.out.println(
new
BigDecimal(
"0.4"
).add(
new
BigDecimal(
"0.8"
)));
//=1.2√
System.out.println(
new
BigDecimal(
"2"
).subtract(
new
BigDecimal(
"1.1"
)))
//=0.9√
System.out.println(
new
BigDecimal(
"0.2"
).multiply(
new
BigDecimal(
"3"
)));
//=0.6√
System.out.println(
new
BigDecimal(
"1.2"
).divide(
new
BigDecimal(
"3"
)));
//=0.4√
}
|
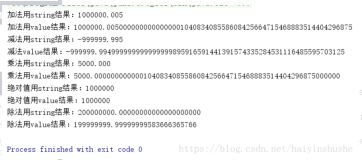
后台打印输出结果:
|
1
2
3
4
|
1.2
0.9
0.6
0.4
|
OK,这下子终于不出篓子了,所以千万不能随随便便使用 BigDecimal(double) 构造器来创建 BigDecimal 对象,因为该构造器是根据它的参数的精确值来创建实例对象的,
该构造方法的结果还是有一定的不可预知性,用 BigDecimal(String) 此构造器来创建 BigDecimal 实例那就不会有问题了。
以上提到了类 BigDecimal 中的 add 、subtract 、multiply 、divide 方法,在 API 中,你可以看到,这几个方法都各自有自己的一个重载方法,如:
add (BigDecimal augend, MathContext mc) ……
第二个参数 mc 是什么意思呢?先来看一段代码:
|
1
2
3
4
5
6
|
public
static
void
main(String[] args){
//计算结果保留两位有效数字
System.out.println(
new
BigDecimal(Math.PI +
""
).add(
new
BigDecimal(
"0.89842"
),
new
MathContext(
2
)));
//输出 4.0
}
|
第二个参数 mc 是用来保留计算结果的有效位数的,其他三个方法的重载用法是一样的,这里就不一 一列出来了。
转自:http://www.blogjava.net/fancydeepin/archive/2012/08/29/java_bigdecimal.html
本文转自 兴趣e族 51CTO博客,原文链接:http://blog.51cto.com/simplelife/1860197