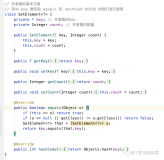
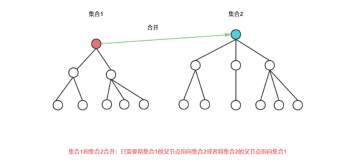
并查集是一种树形的数据结构,用于集合的合并。
与C++STL相比的优势:
- 可以同时维护多个集合
- 快速的合并两个集合
**现实:
用数组实现。father[1000];**
1. 初始化:
for(int i=1;i<=n;++i) father[i]=i; //默认存在n个根,即n个集合。
2. 查找一个元素所在的集合(即查找根)
int get(int a){
if(father[a]==a) return a;
else return get(father[a]);
}这里解释下,数组的下标代表数组的权值,而数组中的值指的是数组所在的父节点。
3.合并两个集合。
void merge(int x,int y){//合并
x=get(x);
y=get(y);
if(x!=y)//先查找两个集合的根,如果根相同,则不合并
father[x]=y;//将集合x的根直接指向集合y的根
}经典例题:
在社交的过程中,通过朋友,也能认识新的朋友。在某个朋友关系图中,假定 A 和 B 是朋友,B 和 C 是朋友,那么 A 和 C 也会成为朋友。即,我们规定朋友的朋友也是朋友。
现在,已知若干对朋友关系,询问某两个人是不是朋友。
请编写一个程序来解决这个问题吧。
输入格式
第一行:三个整数 n,m,p(n≤5000,m≤5000,p≤5000),
分别表示有 n 个人,m 个朋友关系,询问 p 对朋友关系。
接下来 m 行:每行两个数 Ai,Bi1≤Ai,Bi≤N,表示 A i和 Bi具有朋友关系。接下来 p行:每行两个数,询问两人是否为朋友。
输出格式
输出共 p 行,每行一个Yes或No。表示第 i个询问的答案为是否朋友。
样例输入
6 5 3
1 2
1 5
3 4
5 2
1 3
1 4
2 3
5 6
样例输出
Yes
Yes
No
#include<iostream>
using namespace std;
int father[5001];
int get(int a){
if(father[a]==a) return a;
else return get(father[a]);
}
void merge(int x,int y){//合并
x=get(x);
y=get(y);
if(x!=y)
father[x]=y;
}
int main(){
int n,m,p;
cin>>n>>m>>p;
for(int i=1;i<=n;++i) father[i]=i;
for(int i=1;i<=m;++i){
int x,y;
cin>>x>>y;
if(get(x)==get(y)) continue;
merge(x,y);
}
for(int i=1;i<=p;++i){
int x,y;
cin>>x>>y;
if(get(x)==get(y)) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
}