很久没更新博客了,来篇水的。今天看见有位兄弟写了杨辉三角形,记得以前自己也研究过,索性也发一篇,欢迎讨论。
来历
杨辉三角形也叫贾宪三角形,西方叫帕斯卡三角形,其实就是各阶二项式系数排列起来构成的三角形,如下。每行的数字实际上是(a + b) ^ n展开后的结果。
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
历史上发现这个三角形的人很多,这里介绍几个主要的,北宋人贾宪约1050年首先使用“贾宪三角”进行高次开方运算。杨辉,字谦光,南宋时期杭州人。在他1261年所著的《详解九章算法》一书中,辑录了如上所示的三角形数表,称之为“开方作法本源”图。欧洲直到1623年以后,法国数学家帕斯卡在13岁时发现了“帕斯卡三角”。
编程输出杨辉三角形
方法一
使用二维数组计算并存储各行数字然后输出,如果不考虑每行左侧空格的话,上面的三角形可以写成如下形式
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
根据观察我们发现,第一列和对角线上的数字都是1,其他数字则是其左上方数字和正上方数字之和,如下图,其中数字1被标记成红色,因为1是我们预先设置好的,图中的白色数字为合成数字,合成数字是由1或者其他已经存在的数字相加而成的。比如数字2是由其上方的1和左上方的1相加而成,第一个3是由其上方的2和左上方的1相加而成。

设p是存储数字的二维数组,设i和j分别表示p的行号和列号,则有
- 如果j == 0 或 j == i,则p[i][j] = 1 ;
- 否则,p[i][j] = p[i - 1][j] + p[i - 1][j - 1] ;
有了上面的分析,写代码就不再是难事了。
// 打印杨辉三角形,参数n是层数
void YanghuiTriangle( int n)
{
// 定义二维数组并初始化
int ** p = new int * [n] ;
for ( int i = 0 ; i < n; ++ i)
{
p[i] = new int [n] ;
for ( int j = 0 ; j < n; ++ j)
p[i][j] = 0 ;
}
// 填充并输出
for ( int i = 0 ; i < n; ++ i)
{
for ( int j = 0 ; j <= i; ++ j)
{
// 第一列和对角线列的元素置1
if (j == 0 || j == i)
p[i][j] = 1 ;
// 其他元素是其上方元素和左上方元素之和
else
p[i][j] = p[i - 1 ][j] + p[i - 1 ][j - 1 ] ;
cout << p[i][j] << " " ;
}
cout << endl ;
}
}
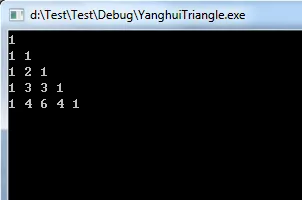
输出如下
方法二
方法一的优点是直观,代码好写,但是缺点是如果层数n很大的话,那么将需要很大的存储空间(n * n),而这么大的空间中有一半被浪费掉了。下面这个方法使用一维数组实现,空间上只要n即可。思路是逐行计算并输出,举个例子,假设我们要输出5行(n = 5),我们先计算并输出第一行,然后计算并输出第二行,...,最后是第五行,因为每行的数字个数不超过行数n,所以一个含有n个元素的一维数组就可以胜任了,只不过这个一维数组中的数字是不断变化的(除了第一个元素),我们用新增的元素覆盖掉了原来的元素。下图展示了这个一维数组的变化过程。其中红色字数字表示每次迭代新增的数字。可见这种方法中第一列数字1始终保持不变。

1 首先定义一个含有n个元素的一维数组,且第一个元素初始化为1,其他元素初始化为0
2 对于每一行的计算,除了第一元素之外,其他所有元素都由其本身的值加上其前一个值构成,注意,计算的方向是从后向前,如果从前向后的话,元素本来的值将被覆盖。
代码如下
// 打印杨辉三角形,参数n是层数
void YanghuiTriangle( int n)
{
// 定义一个一维数组
int * a = new int [n] ;
for ( int i = 0 ; i < n; ++ i)
a[i] = 0 ;
a[ 0 ] = 1 ;
for ( int i = 0 ; i < n; ++ i)
{
// 计算当前行的数字,注意要从后向前计算,否则会覆盖以前的值
for ( int j = i; j > 0 ; -- j)
a[j] += a[j - 1 ];
// 打印空格
for ( int j = 0 ; j < n - i; ++ j)
cout << " " ;
// 打印数字
for ( int j = 0 ; j < i + 1 ; ++ j)
cout << a[j] << " " ;
cout << endl ;
}
}
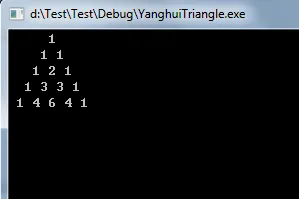
输出如下,因为处理了空格,所以更美观一点。
Happy Coding!!!
== THE END ==
本文转自zdd博客园博客,原文链接:http://www.cnblogs.com/graphics/archive/2011/07/11/2103117.html,如需转载请自行联系原作者


