1 博弈树搜索(深度优先搜索)
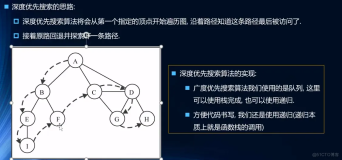
博弈树搜索是人工智能领域中一种重要的算法,常用于制定决策和策略的制定,特别是在博弈和决策问题中。这种搜索方法基于树形结构,其中每个节点表示一个游戏状态或决策点,而边则代表可能的行动或决策。通过深度优先搜索或广度优先搜索,算法可以遍历博弈树,评估每个节点的价值,并最终选择最优的决策路径。
在博弈树搜索中,常见的应用场景包括棋类游戏(如国际象棋、围棋、井字棋等)和其他多人参与的博弈情境。算法的目标是为当前玩家找到一种最优的策略,使得在对手采取最佳应对的情况下,当前玩家能够取得最大的收益。
每个节点的状态由游戏中的各种因素确定,例如棋盘上的布局、剩余的游戏步数、玩家的分数等。通过递归地评估每个可能的决策,博弈树搜索能够构建一个全面的决策树,其中包含了游戏中所有可能的决策路径。
博弈树搜索的核心思想是利用深度优先或广度优先搜索算法,通过递归地遍历树结构,评估每个节点的局势,并根据评估结果选择最有利的决策。在这一过程中,算法需要考虑到对手的最佳应对,以确保制定的策略在各种情况下都具有鲁棒性。
在实际应用中,博弈树搜索为计算机在复杂决策问题中找到最优解提供了一种强大而灵活的方法。通过不断优化算法和引入剪枝等技术,博弈树搜索在人工智能领域的许多成功案例中发挥着重要作用。
二叉树:表示初始化和创建二叉树节点的过程
执行深度优先搜索:表示深度
表示从二叉树构建链表的过程 表示链接中的值打印
3 核心代码
struct TreeNodestruct ListNode
这些结构定义了二叉树和链表的基本构建块:
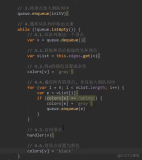
深度优先搜索
dfs是一个递归深度优先搜索函数,它遍历二叉树并按预序打印节点的值。
构建链表函数(buildLinkedList)
根据二叉树的深度优先搜索顺序构造链表。它返回链表的头部。
4 代码结果
深度优先搜索 (DFS) 输出: 1 2 4 5 3 6 7
显示二叉树的深度优先搜索遍历的结果。顺序是预序遍历(root、left、right)。
单链表的节点值: 1 2 4 5 3 6 7
显示链表节点的值。链表是根据深度优先搜索期间访问的节点顺序构建的。
5 算法优缺点
该算法在二叉树上执行深度优先搜索(DFS)遍历,并根据DFS遍历的顺序构造链表。以下是优点和缺点以及时间复杂度:
优势:
单纯:该算法相对易于理解和实现。
内存效率:该算法不需要额外的空间来存储中间结果(除非在 DFS 期间考虑递归调用堆栈)。链表的构造方式直接使用现有的树节点。
弊端:
内存管理:该算法使用手动内存管理 ( 和 ) 来构建和删除节点。这可能容易出错,如果不小心操作,可能会导致内存泄漏或分段错误。现代 C++ 提供了智能指针等工具来缓解这些问题。newdelete
时间复杂度:
DFS 遍历的时间复杂度为 O(N),其中 N 是二叉树中的节点数。每个节点访问一次。
构建链表的时间复杂度也是 O(N),其中 N 是节点数。这是因为每个节点都访问一次,并且每个节点都会完成恒定的工作量。
6 附件之源代码
#include <iostream>
// 节点结构
struct TreeNode {
int value;
TreeNode* left;
TreeNode* right;
TreeNode(int val) : value(val), left(nullptr), right(nullptr) {
}
};
// 单链表结构
struct ListNode {
TreeNode* node;
ListNode* next;
ListNode(TreeNode* n) : node(n), next(nullptr) {
}
};
// 深度优先搜索函数
void dfs(TreeNode* node) {
if (node == nullptr) {
return;
}
std::cout << node->value << " ";
dfs(node->left);
dfs(node->right);
}
// 根据深度优先搜索构建单链表
ListNode* buildLinkedList(TreeNode* root) {
if (root == nullptr) {
return nullptr;
}
ListNode* head = new ListNode(root);
ListNode* current = head;
if (root->left != nullptr) {
current->next = buildLinkedList(root->left);
while (current->next != nullptr) {
current = current->next;
}
}
if (root->right != nullptr) {
current->next = buildLinkedList(root->right);
}
return head;
}
// 释放单链表内存
void deleteLinkedList(ListNode* head) {
while (head != nullptr) {
ListNode* temp = head;
head = head->next;
delete temp->node; // 释放节点内存
delete temp; // 释放链表节点内存
}
}
int main() {
// 构建一个简单的二叉树
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(5);
root->right->left = new TreeNode(6);
root->right->right = new TreeNode(7);
// 深度优先搜索
std::cout << "深度优先搜索: ";
dfs(root);
std::cout << std::endl;
// 构建单链表
ListNode* linkedList = buildLinkedList(root);
// 输出单链表的节点值
std::cout << "单链表的节点值: ";
ListNode* current = linkedList;
while (current != nullptr) {
std::cout << current->node->value << " ";
current = current->next;
}
std::cout << std::endl;
// 释放内存
deleteLinkedList(linkedList);
delete root;
return 0;
}