前言:
今天我们开始学习排序。为了方便大家理解和练习,排序一共分为两节进行讲解,在该章节中会复习学习过的排序,和讲解新的排序,还望读者能从中得到良好的体验。
一、冒泡排序
冒泡排序作为基础排序,在我们学习C语言过程中,第一位教给我们排序的老师。其实现过程如下:
冒泡排序可以说是很经典的交换排序。各位读者此时对于此排序的实现应该没多大问题,就不过多讲解,直接上代码:
// 冒泡排序 void BubbleSort(int* a, int n) { for (int j = 0; j < n; j++) { for (int i = 0; i < n - 1 - j; i++) { if (a[i] > a[i + 1]) { sweap(&a[i], &a[i + 1]); } } } }
我们直到其实现逻辑就是逐一比较。那么,我们能否对其进行优化,即:在有序的情况下减少其比较次数以提高运行效率。
为了解决这个问题我们可以这样想:咱们可以通过什么来判断其是有序的?程序又不像咱们一样拥有上帝视角,它比较呆,只能通过指令执行。通过观察上面的动图我们可以得出这样的结论:当没发生任何交换时,是有序的。那么,我们按此思路可以这样做:定义一个标识符,如果标识符未发生改变,我们即可认为它有序,然后break跳出循环。代码实现如下:
// 冒泡排序 void BubbleSort(int* a, int n) { for (int j = 0; j < n; j++) { int flag = 1;//定义标识符 for (int i = 0; i < n - 1 - j; i++) { if (a[i] > a[i + 1]) { flag = 0; sweap(&a[i], &a[i + 1]); } } if (flag == 1)//当不发生交换时停止 { break; } } }
二、选择排序
选择排序可以认为是冒泡的难兄难弟,执行效率稍逊色于冒泡。那么,什么是选择排序呢?各位读者肯定都站过队,站队的过程类似于选择排序,小的往前和大的往后是同时发生的。以下动图帮助大家理解:
不同于动图的是,我们可以同时实现放大和放小。即,每次遍历记录最大和最小下标,然后交换以此类推。代码实现如下:
// 选择排序 void SelectSort(int* a, int n) { int begin = 0; int end = n - 1; while (begin < end) { int min = begin; int max = begin; for (int i = begin + 1; i <= end; i++)//i从begin开始也行,但与自己比较意义不大 { if (a[i] > a[max]) { max = i; } if (a[i] < a[min]) { min = i; } } sweap(&a[begin], &a[min]); sweap(&a[end], &a[max]); begin++; end--; } }
这便是选择排序的代码,我们此时进入下一个排序吧!你们觉得合适吗?当然不合适,相信聪明的读者已经发现以上代码存在bug了。什么问题?即:当max与begin的下标相同时,最小值会被当做最大值换到后面。
那,该问题如何解决?很简单,加上一个判断,当begin与max的下标相同时,max = min。因为:此时最大值的下标为:min。
正确代码如下:
// 选择排序 void SelectSort(int* a, int n) { int begin = 0; int end = n - 1; while (begin < end) { int min = begin; int max = begin; for (int i = begin + 1; i <= end; i++)//i从begin开始也行,但与自己比较意义不大 { if (a[i] > a[max]) { max = i; } if (a[i] < a[min]) { min = i; } } sweap(&a[begin], &a[min]); if (begin == max) { max = min; } sweap(&a[end], &a[max]); begin++; end--; } }
三、堆排序
堆排序前面我们已经讲解过,这里简单介绍一下。
堆排序的实现思想为:我们在排升序时,建大堆;排降序,建小堆。把堆建好后,把堆头元素与堆尾元素进行交换,交换后运用向下调整进行调整,直到排列完毕。
代码实现如下:
// 堆排序 void AdjustDwon(int* a, int n, int parent) { int child = parent * 2 + 1; while (child < n) { if (child + 1 < n && a[child] > a[child + 1]) { child++; } if (a[parent] > a[child]) { sweap(&a[parent], &a[child]); parent = child; child = parent * 2 + 1; } else { break; } } } void HeapSort(int* a, int n) { for (int i = (n - 1 - 1) / 2; i >= 0; i--) { AdjustDwon(a, n, i); } int end = n - 1; while (end) { sweap(&a[0], &a[end]); AdjustDwon(a, end, 0); end--; } }
具体讲解可看:二叉树——堆详解-CSDN博客
四、插入排序
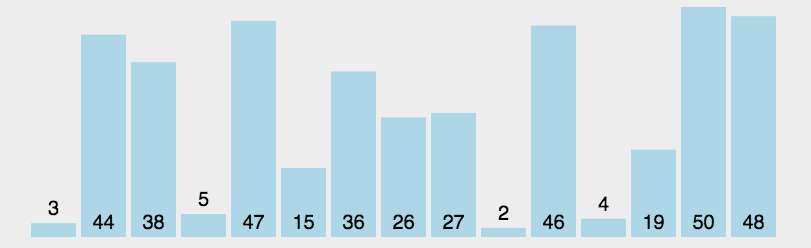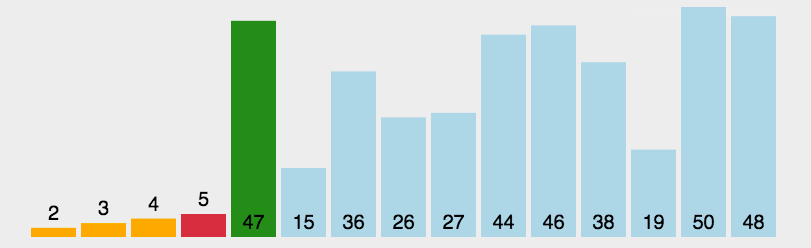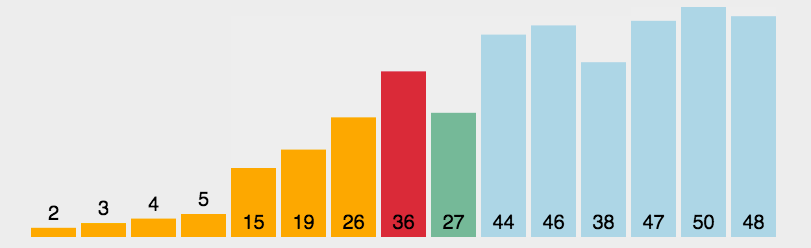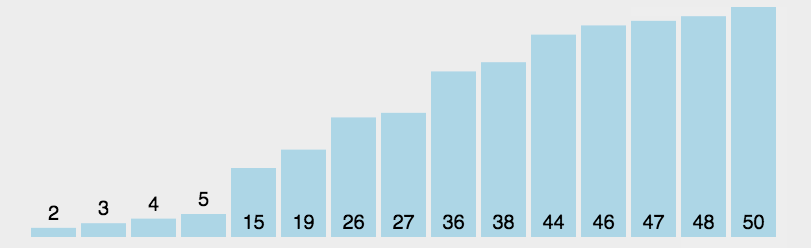
接下来,我们要学习的为:插入排序。那么?什么为插入排序呢?各位读者可参考如下动图:
插入排序:第n个数据依次与前面数据比较,如果比前面小(升序)便插到该数据前面,反之,结束本次循环。
所以,写此排序的实现思路很明确了:记录某个数据的值和它前面的依次比较,如果满足条件,传位于它,自己继续负重前行。
在我们写排序时,如果稍不注意就会出错,那么,我们该如何降低出错概率呢?答案为:先写单趟,再写整体。
现在,我们有了实现思路,又有了写的方法。各位读者试着自己去写一写,或参考如下代码,再独立实现。
// 插入排序 void InsertSort(int* a, int n) { for (int i = 0; i < n - 1; i++) { int end = i; int tmp = a[end + 1]; while (end >= 0) { if (a[end] > tmp) { a[end + 1] = a[end]; end--; } else { break; } } a[end + 1] = tmp; } }
五、希尔排序
希尔排序是啥?希尔排序是一个人对于插入排序的改良版,那看到这了,不禁要问:那个大佬是谁?这不,名字不就告诉我们答案了。就是这位大佬,改良了插入排序,使得效率大幅提升。那么,是如何改良的呢?且听我,娓娓道来。
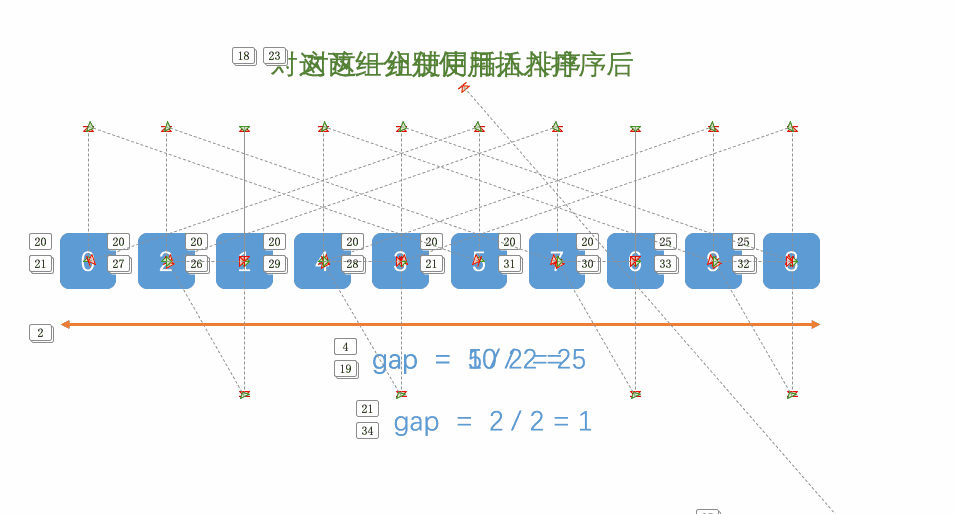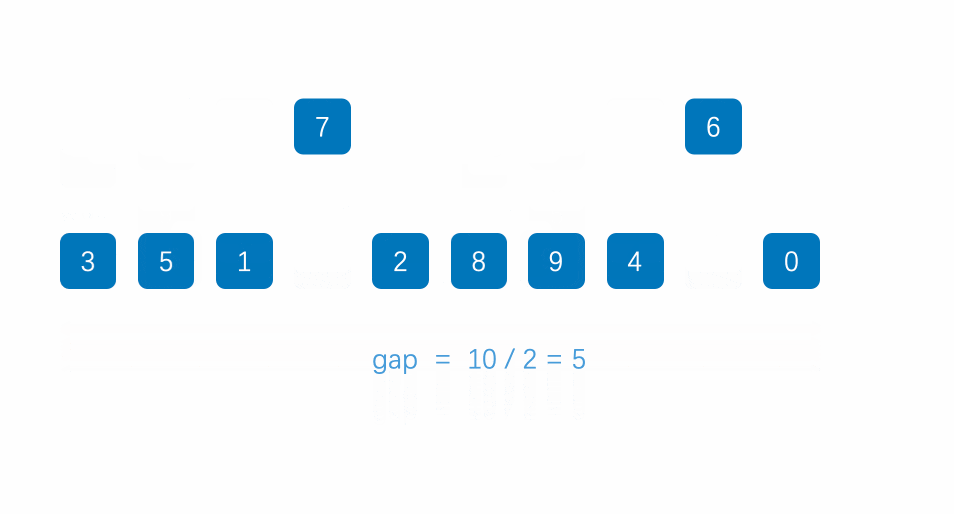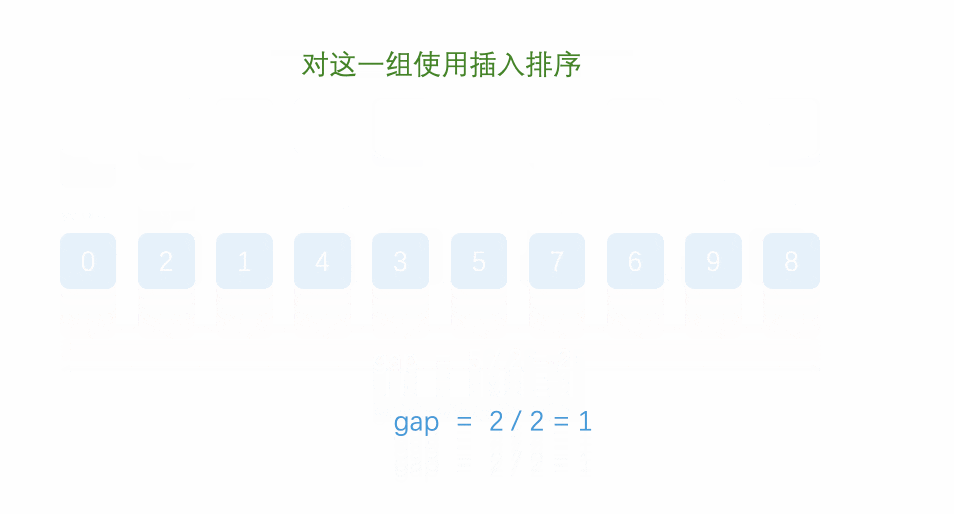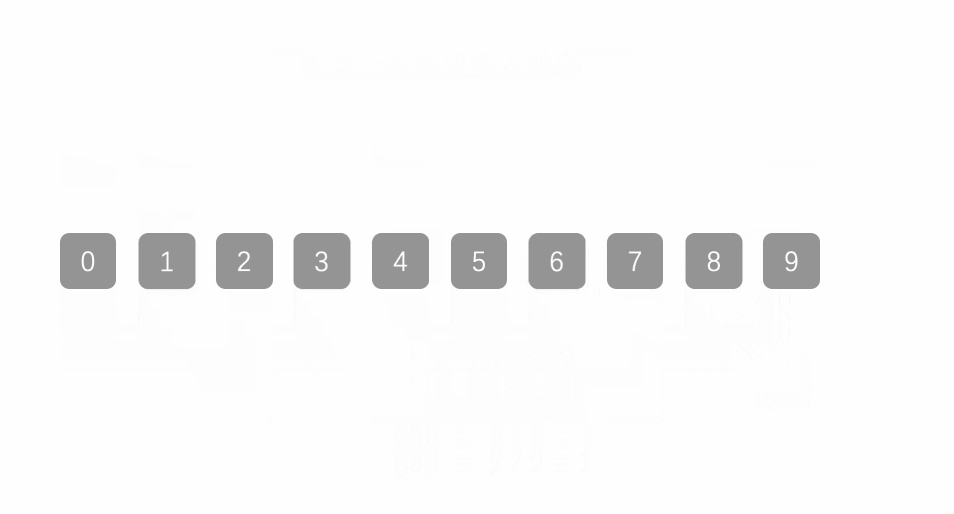
希尔排序比插入排序多了:预排序这个阶段。其作用就是使该数组更接近有序。
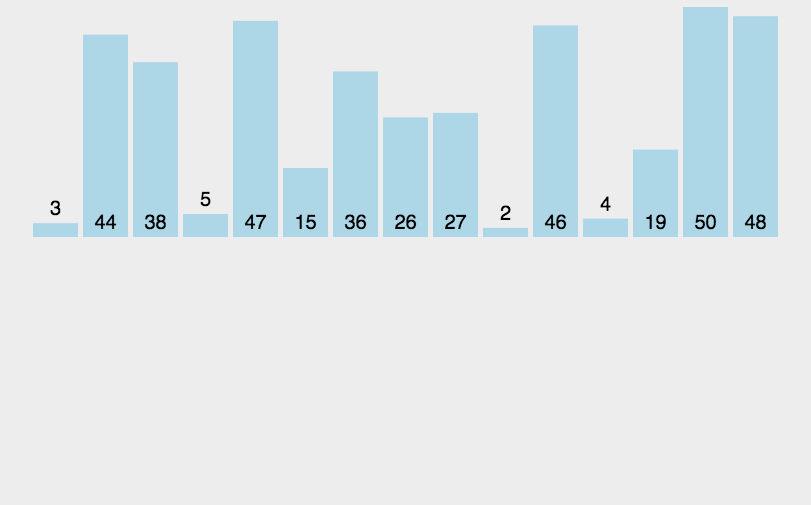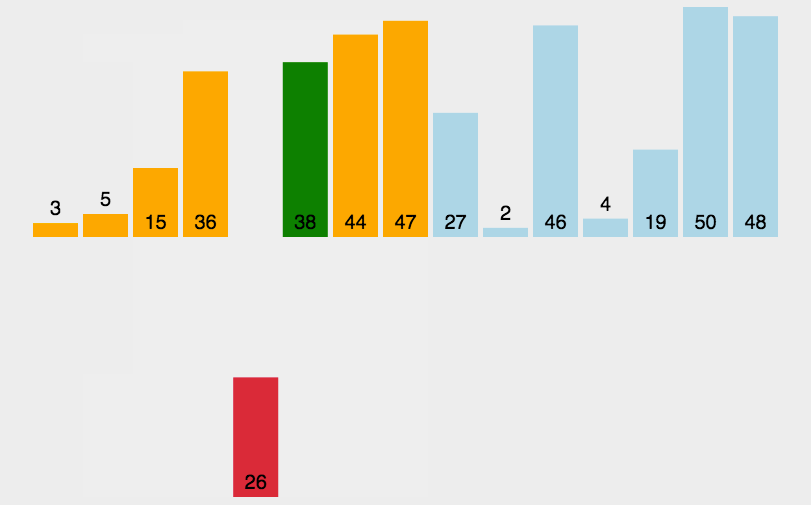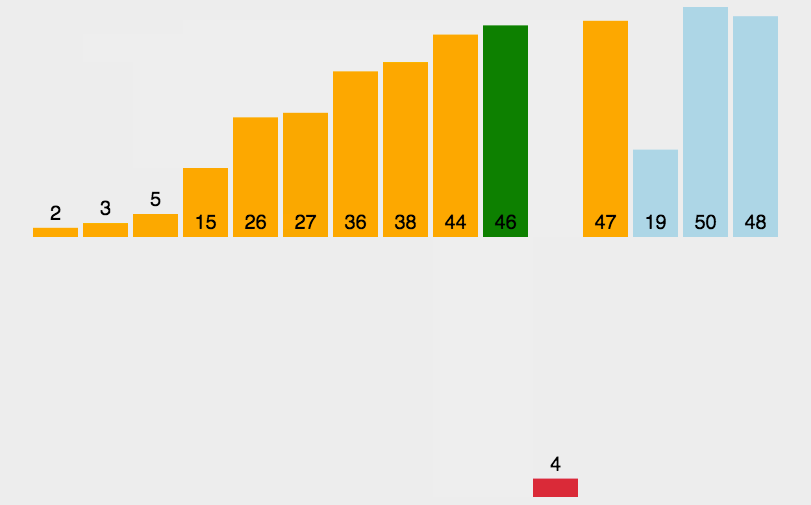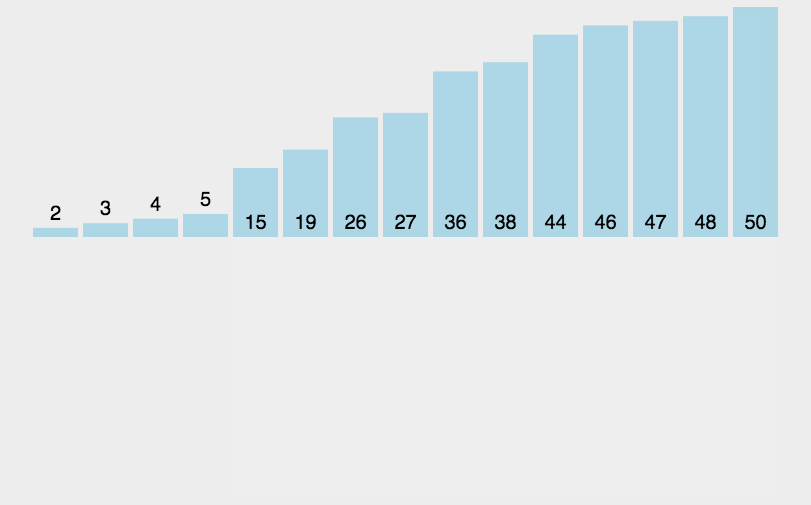
那该如何进行预排序呢?我们可看插入排序,插入排序每次增加1,那大的数跑到后面是不是太慢了,那,我每次跑2或3是不是可以使该排序的数组大的数据迅速向后移动,虽然整体还是无序,但对于大部分的大数都集中于后方,小一点的数集中于前方。对吧?可结合以下图片和动图理解。
那么,什么时候能判断 其是有序的?答案为:grap == 1 时,虽然最后一次看似是插入排序,实则不是。它相对于插入排序更加的有序,效率也大大提升。
那,看到这我们不禁要问:那grap的取值有规定吗?没有。但是有人研究过:当grap为3时效率最高。其时间复杂度为:O(N^1.3)。各位记住即可,本博主的数学水平,不支持进行推导。
明白了这些,下面是代码的实现,可结合进行理解:
// 希尔排序 void ShellSort(int* a, int n) { int gap = n; while (gap > 1) { // +1保证最后一个gap一定是1 // gap > 1时是预排序 // gap == 1时是插入排序 gap = gap / 3 + 1; for (int i = 0; i < n - gap; i++) { int end = i; int tmp = a[end + gap]; while (end >= 0) { if (tmp < a[end]) { a[end + gap] = a[end]; end -= gap; } else { break; } } a[end + gap] = tmp; } } }
六、代码总览
#include<stdio.h> void sweap(int* p1, int* p2) { int tmp = *p1; *p1 = *p2; *p2 = tmp; } // 冒泡排序 void BubbleSort(int* a, int n) { for (int j = 0; j < n; j++) { int flag = 1; for (int i = 0; i < n - 1 - j; i++) { if (a[i] > a[i + 1]) { flag = 0; sweap(&a[i], &a[i + 1]); } } if (flag == 1) { break; } } } // 插入排序 void InsertSort(int* a, int n) { for (int i = 0; i < n - 1; i++) { int end = i; int tmp = a[end + 1]; while (end >= 0) { if (a[end] > tmp) { a[end + 1] = a[end]; end--; } else { break; } } a[end + 1] = tmp; } } // 希尔排序 void ShellSort(int* a, int n) { int gap = n; while (gap > 1) { // +1保证最后一个gap一定是1 // gap > 1时是预排序 // gap == 1时是插入排序 gap = gap / 3 + 1; for (int i = 0; i < n - gap; i++) { int end = i; int tmp = a[end + gap]; while (end >= 0) { if (tmp < a[end]) { a[end + gap] = a[end]; end -= gap; } else { break; } } a[end + gap] = tmp; } } } // 选择排序 void SelectSort(int* a, int n) { int begin = 0; int end = n - 1; while (begin < end) { int min = begin; int max = begin; for (int i = begin + 1; i <= end; i++)//i从begin开始也行,但与自己比较意义不大 { if (a[i] > a[max]) { max = i; } if (a[i] < a[min]) { min = i; } } sweap(&a[begin], &a[min]); if (begin == max) { max = min; } sweap(&a[end], &a[max]); begin++; end--; } } // 堆排序 void AdjustDwon(int* a, int n, int parent) { int child = parent * 2 + 1; while (child < n) { if (child + 1 < n && a[child] > a[child + 1]) { child++; } if (a[parent] > a[child]) { sweap(&a[parent], &a[child]); parent = child; child = parent * 2 + 1; } else { break; } } } void HeapSort(int* a, int n) { for (int i = (n - 1 - 1) / 2; i >= 0; i--) { AdjustDwon(a, n, i); } int end = n - 1; while (end) { sweap(&a[0], &a[end]); AdjustDwon(a, end, 0); end--; } }
最后:
以上便是本文的内容,希尔排序看着抽象,实际也不好理解,大家下去要多画图进行理解。其余的排序会在后续文章发出,期待下篇文章再见。