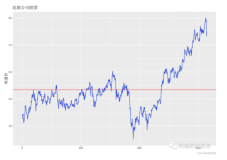
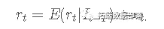在这里,我将用R中的一个小模拟示例进行说明。首先,我们使用X1和X2双变量法线和Y模拟大型数据集,其中Y遵循给定X1和X2的逻辑模型。
首先,我们模拟一个非常大的完整数据集:
#simulate完整数据 expit < - function(x){ EXP(X)/(1 + EXP(X)) } n < - 100000 x < - mvrnorm(n,mu = c(0,0),Sigma =(c(1,0.2,0.2,1),nrow = 2)) x1 < - x [,1] x2 < - x [,2] y < - 1 *(runif(n)<expit(-3 + log(3)* x1 + log(3)* x2)) (Y) [1] 0.11052
接下来,我们估计将X1从1更改为0的影响的边际风险比:
#estimate x1 = 1 vs x1 = 0的边际风险比,标准化为完整数据 #以后用于MI,我们将编写一个获取数据集并返回此估计值的函数 marginalRiskRatio < - function(inputData){ ymod < - glm(y~x1 + x2,family =“binomial”,data = inputData) #predict风险在x1 = 0下 x1 = 1下的#predict risk risk1 < - expit(coef(ymod)[1] + coef(ymod)[2] * 1 + (ymod)[3] * inputData $ x2) #estimate边际风险比率 (risk1)/(risk0) } fullData < - data.frame(y = y,x1 = x1,x2 = x2) marginalRiskRatio(fullData) [1] 2.295438
接下来,我们使用Sullivan 等人考虑的一种机制,在Y和X2中缺少一些值:
z1 < - x1 / 0.2 ^ 0.5 r_y < - 1 *(runif(n)<expit(2.5 + 2 * z1)) r_x2 < - 1 *(runif(n)<expit(2.5 + 2 * z1)) obsData < - fullData obsData $ y [r_y == 0] < - NA obsData $ x2 [r_x2 == 0] < - NA
现在我们可以在Y和X2中估算缺失的值。指定逻辑结果模型的缺失结果以及来自与逻辑结果模型兼容的插补模型的缺失协变量值:
numImps < - 10 imps < - (obsData,smtype =“logistic”,smformula =“y~x1 + x2”, method = c(“”,“”,“norm”),m = numImps) [1] "Outcome variable(s): y" [1] "Passive variables: " [1] "Partially obs. variables: x2" [1] "Fully obs. substantive model variables: x1" [1] "Imputation 1" [1] "Imputing missing outcomes using specified substantive model." [1] "Imputing: x2 using x1 plus outcome" [1] "Imputation 2" [1] "Imputation 3" [1] "Imputation 4" [1] "Imputation 5" [1] "Imputation 6" [1] "Imputation 7" [1] "Imputation 8" [1] "Imputation 9" [1] "Imputation 10" Warning message: In smcfcs.core(originaldata, smtype, smformula, method, predictorMatrix, : Rejection sampling failed 7 times (across all variables, iterations, and imputations). You may want to increase the rejection sampling limit.
最后,我们可以应用我们之前定义的函数来估算每个估算数据集的边际风险比,并使用鲁宾规则(即采用对数风险比的平均值)将它们结合起来:
estLogRR <- array(0, dim=numImps) for (i in 1:numImps) { [i] <- log(marginalRiskRatio(imps$impDatasets[[i]])) } #pooled estimate of log risk ratio is mean(estLogRR) [1] 0.8325685 #and estimate of risk ratio exp(mean(estLogRR)) [1] 2.299217
我们在插补后得到一个非常接近完整数据估计的估计值。