今天笔记内容包含R语言中矩阵和数组基础知识。
R语言矩阵
创建矩阵
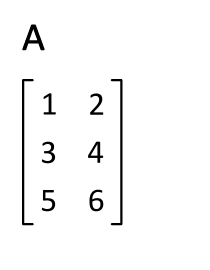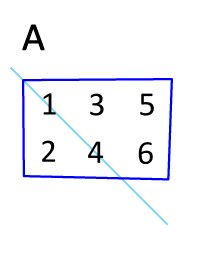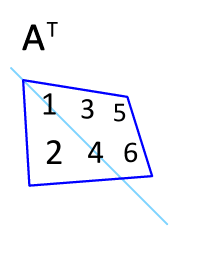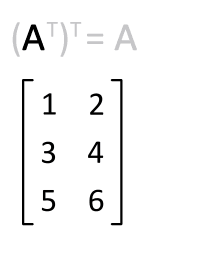
矩阵内可以是数字、符号、数学式,类似于常见的二维数组,有m行(row)n列(col)的矩阵m×n。
R 语言的矩阵可以使用 matrix() 函数来创建,语法格式如下:matrix(data = NA, nrow = 1, ncol = 1, byrow = FALSE,dimnames = NULL)
参数说明:
- data 向量,矩阵的数据
- nrow 行数
- ncol 列数
- byrow 逻辑值,为 FALSE 按列排列,为 TRUE 按行排列
- dimname 设置行和列的名称,该参数用含有两个向量(字符串)的列表组成。
> # 按行排列创建矩阵 > zhen_1 = matrix(c(1:12),nrow = 3,byrow = TRUE) > print(zhen_1) [,1] [,2] [,3] [,4] [1,] 1 2 3 4 [2,] 5 6 7 8 [3,] 9 10 11 12 > # 定义行和列的名称 > rownames_1 = c("a1","a2","a3") > colnames_2 = c("b1","b2","b3","b4") > # 输出矩阵 > out_1 = matrix(c(1:12),nrow = 3,byrow = TRUE,dimnames = list(rownames_1,colnames_2)) > print(out_1) b1 b2 b3 b4 a1 1 2 3 4 a2 5 6 7 8 a3 9 10 11 12
转置矩阵
R 语言矩阵提供了t()函数,可以实现矩阵的行列互换,变化效果如下:我们对刚刚创建的out_1矩阵进行转置后输出,如下:
> out_1 = matrix(c(1:12),nrow = 3,byrow = TRUE,dimnames = list(rownames_1,colnames_2)) > print(out_1) b1 b2 b3 b4 a1 1 2 3 4 a2 5 6 7 8 a3 9 10 11 12 > print(t(out_1)) #输出转置矩阵用t() a1 a2 a3 b1 1 5 9 b2 2 6 10 b3 3 7 11 b4 4 8 12
调用矩阵元素
可以元素的列索引和行索引,类似坐标形式,获取矩阵元素,如下:
> print(out_1) #获取整个矩阵 b1 b2 b3 b4 a1 1 2 3 4 a2 5 6 7 8 a3 9 10 11 12 > print(out_1[1,2]) # 获取第1行第2列的元素 [1] 2 > print(out_1[2,]) # 获取第2行的元素 b1 b2 b3 b4 5 6 7 8
矩阵的计算
大部分人已经学过线性代数,了解矩阵的加减乘除法则,值得注意的是只有行和列数都相同的矩阵才能加减运算,只有第一个矩阵的列数等于第二个矩阵的行数才能相乘。接下来进行演示:
> # 矩阵相加,相减只需把加号改成减号 > out_sum = m_1 + m_2 # 两个矩阵都是2×3 > cat("结果:","\n") 结果: > print(out_sum) [,1] [,2] [,3] [1,] 14 -2 4 [2,] 18 8 6 > # 矩阵相乘 > out_cheng = m_1 * m_2 > cat("结果:","\n") 结果: > print(out_cheng) [,1] [,2] [,3] [1,] 49 1 4 [2,] 81 16 9 > # 矩阵相除 > out_chu = m_1 / m_2 > cat("结果:","\n") 结果: > print(out_chu) [,1] [,2] [,3] [1,] 1 1 1 [2,] 1 1 1
数组
R 语言可以创建一维或多维数组,数组是一个同一类型的集合,矩阵就是一个二维数组。
数组创建使用array()函数,该函数使用向量作为输入参数,可以使用 dim 设置数组维度。语法格式如下:
array(data = NA, dim = length(data), dimnames = NULL)
- data 向量,数组元素。
- dim 数组的维度,默认是一维数组。
- dimnames 维度的名称,必须是个列表
例如创建一个3×3的二维数组,用于后续演示,方法如下:
> v1 = c(1,2,3) > v2 = c(4,5,6,7,8,9) > shuzu = array(c(v1,v2),dim = c(3,3,2)) > print(shuzu) , , 1 [,1] [,2] [,3] [1,] 1 4 7 [2,] 2 5 8 [3,] 3 6 9 , , 2 [,1] [,2] [,3] [1,] 1 4 7 [2,] 2 5 8 [3,] 3 6 9
- 设置各维度的名称
> column.names = c("col1","col2","col3") #设置列名 > row.names = c("row1","row2","row3") #设置行名 > matrix.names = c("m1","m2") #设置矩阵名 > out_3 = array(c(v1,v2),dim = c(3,3,2),dimnames = list(row.names,column.names,matrix.names)) #设置数组名 > print(out_3) #输出 , , m1 col1 col2 col3 row1 1 4 7 row2 2 5 8 row3 3 6 9 , , m2 col1 col2 col3 row1 1 4 7 row2 2 5 8 row3 3 6 9 #上述m1和m2矩阵应用于笔记后面的演示,不再重复
- 访问数组元素
数组的元素有坐标位置,索引顺序为(行,列,维度),例如[3,2,4]表示第4个矩阵第3行第2列的元素。
, , m2 #第二个矩阵 col1 col2 col3 row1 1 4 7 row2 2 5 8 row3 3 6 9 > print(out_3[3,1,2]) [1] 3 #输出结果正确
- 操作数组元素
可以通过访问矩阵的元素来访问数组,例如从数组中的一个矩阵创建新矩阵,然后进行矩阵加减运算,演示如下:
> matrix_1 = shuzu[,,1] > matrix_2 = shuzu[,,2] > sum_1 = matrix_1 + matrix_2 > print(sum_1) [,1] [,2] [,3] [1,] 2 8 14 [2,] 4 10 16 [3,] 6 12 18
apply()函数能够对数组跨纬度计算,语法格式为:apply(x, margin, fun)
- x 数组
- margin 数据名称(1代表行,2代表列,c(1,2)代表行和列)
- fun 计算函数
> print(shuzu) , , 1 #数组的第一个矩阵 [,1] [,2] [,3] [1,] 1 4 7 [2,] 2 5 8 [3,] 3 6 9 , , 2 #数组的第二个矩阵 [,1] [,2] [,3] [1,] 1 4 7 [2,] 2 5 8 [3,] 3 6 9 > out_4 = apply(shuzu,1,sum) #对数组所有矩阵按照每一行的方式求和 > print(out_4) [1] 24 30 36 #第一行数据24=1+4+7+1+4+7,确实能行! 快速记忆: # 计算数组中所有矩阵对应行的数字之和 result <- apply(shuzu, c(1), sum) # 计算数组中所有矩阵对应列的数字之和 result <- apply(shuzu, c(2), sum) # 计算数组中每个矩阵内部的所有数字之和 result <- apply(shuzu, c(3), sum)