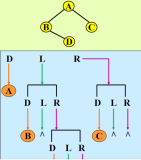
二叉树的定义是用递归定义的,这样我们会发现在它在前中后遍历、甚至插入、建立程序中常常用到递归,实际上把握好了递归,也就把握好了二叉树的遍历问题。
下面是一些问题练习
1.从一个遍历(明确空树)中确定树
时间限制: 1 Sec 内存限制: 32 MB
提交: 312 解决: 186
[提交][状态][讨论版][命题人:外部导入]
题目描述
编一个程序,读入用户输入的一串先序遍历字符串,根据此字符串建立一个二叉树(以指针方式存储)。
例如如下的先序遍历字符串:
ABC##DE#G##F###
其中“#”表示的是空格,空格字符代表空树。建立起此二叉树以后,再对二叉树进行中序遍历,输出遍历结果。
输入
输入包括1行字符串,长度不超过100。
输出
可能有多组测试数据,对于每组数据,
输出将输入字符串建立二叉树后中序遍历的序列,每个字符后面都有一个空格。
每个输出结果占一行。
样例输入
a#b#cdef#####
a##
样例输出
a b f e d c
a
分析:
这个问题其实简单,题目是给出了前序遍历的输入,如果我们也跟着前序遍历,过程中再建立树,题目就可解了,不过得注意边界条件发生了变化。
#include<iostream> #include<string> using namespace std; string s; int i,n; //用来记录字符串位置和大小 struct node{ char data; node *lchild,*rchild; }; node* Create(){ //和前序遍历过程很类似 if(s[i]=='#'){ //边界条件 i++; return NULL; } node* root=new node; root->data=s[i]; i++; if(i<n) //边界条件,可以一起写在上面 root->lchild=Create(); if(i<n) root->rchild=Create(); return root; } void inorder (node* root){ //中序遍历 if(root==NULL)return; inorder(root->lchild); printf("%c ",root->data); inorder(root->rchild); } int main(){ while(cin>>s) { i=0; n=s.length(); node* root=Create(); inorder(root); cout<<endl; } return 0; }
2.从两个遍历确定树
题目描述
小明在做数据结构的作业,其中一题是给你一棵二叉树的前序遍历和中序遍历结果,要求你写出这棵二叉树的后序遍历结果。
输入
输入包含多组测试数据。每组输入包含两个字符串,分别表示二叉树的前序遍历和中序遍历结果。每个字符串由不重复的大写字母组成。
输出
对于每组输入,输出对应的二叉树的后续遍历结果。
样例输入
DBACEGF ABCDEFG
BCAD CBAD
样例输出
ACBFGED
CDAB
分析:
先序第一个是根结点,在中序中找到后划分左右子树,左右子树的长度可知,因为先序遍历中是根左右排布,所以也可以得到左右子树区间,再分区间递归解决即可。
#include<iostream> #include<cstring> using namespace std; const int maxn=40; char a[maxn] ,b[maxn]; struct node{ char data; node *lchild,*rchild; }; node* create(int prel,int preh,int inl,int inh){ if(prel>preh){ 边界条件 return NULL; } node* root=new node; root->data=a[prel]; int k; for(int i=inl;i<=inh;i++) if(a[prel]==b[i]){ k=i; //找到中序遍历中根结点位置 break; } int newpreh=k-inl+prel;//先序中左右子树临界点 root->lchild=create(prel+1,newpreh,inl,k-1); root->rchild=create(newpreh+1,preh,k+1,inh); } void postsearch(node* root){ //后序遍历 if(root==NULL)return; postsearch(root->lchild); postsearch(root->rchild); cout<<root->data; } int main(){ node* root; while(cin>>a>>b){ int i=strlen(a); root=create(0,i-1,0,i-1); postsearch(root);cout<<endl; } return 0; }